【图】图的存储结构
| 邻接矩阵表示法 |
| 邻接矩阵表示法的 C 语言描述 |
#define MAX_VERTEX_NUM 20 /*最多顶点个数*/
#define INFINITY 32768 /*表示极大值，即∞*/
/* 图的种类：DG 表示有向图, DN 表示有向网, UDG 表示无向图, UDN 表示无向网 */
typedef enum
{
DG,
DN,
UDG,
UDN
} GraphKind;
typedef char VertexData; /*假设顶点数据为字符型*/
typedef struct ArcNode
{
AdjType adj; /* 对于无权图，用 1 或 0 表示是否相邻； 对带权图，则为权值类型 */
OtherInfo info;
} ArcNode;
typedef struct
{
VertexData vertex[MAX_VERTEX_NUM]; /*顶点向 量*/
ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; /*邻接矩阵*/
int vexnum, arcnum; /*图的顶点数和弧数*/
GraphKind kind; /*图的种类标志*/
} AdjMatrix; /*（Adjacency Matrix Graph）*/
| 邻接矩阵表示法的特点 |
| 用邻接矩阵法创建有向网的算法 |
int LocateVertex(AdjMatrix *G, VertexData v) /*求顶点位置函数*/
{
int j = Error, k;
for (k = 0; k < G->vexnum; k++)
if (G->vertex[k] == v)
{
j = k;
break;
}
return (j);
}
int CreateDN(AdjMatrix *G) /*创建一个有向网*/
{
int i, j, k, weight;
VertexData v1, v2;
scanf("%d,%d", &G->arcnum, &G->vexnum); /*输入图的顶点数和弧数*/
for (i = 0; i < G->vexnum; i++) /*初始化邻接矩阵*/
for (j = 0; j < G->vexnum; j++)
G->arcs[i][j].adj = INFINITY;
for (i = 0; i < G->vexnum; i++)
scanf("%c", &G->vertex[i]); /* 输入图的顶点*/
for (k = 0; k < G->arcnum; k++)
{
scanf("%c,%c,%d", &v1, &v2, &weight); /*输入一条弧的两个顶点及权 值*/
i = LocateVex_M(G, v1);
j = LocateVex_M(G, v2);
G->arcs[i][j].adj = weight; /*建立弧*/
}
return (Ok);
}
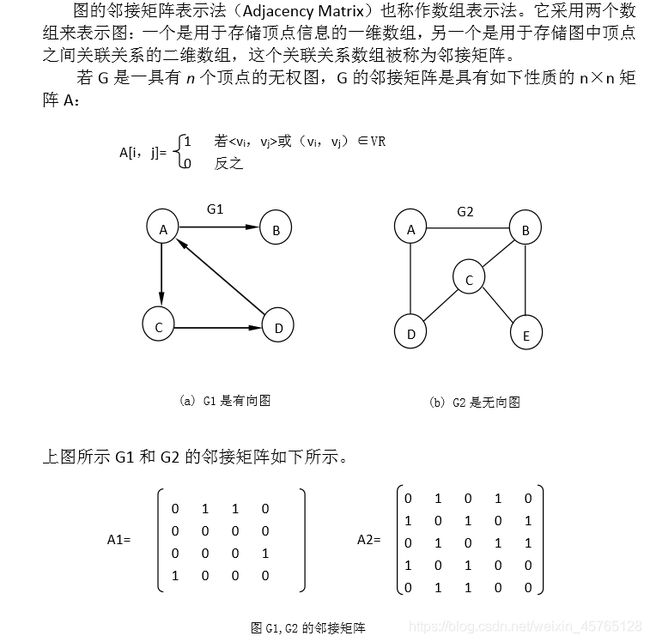
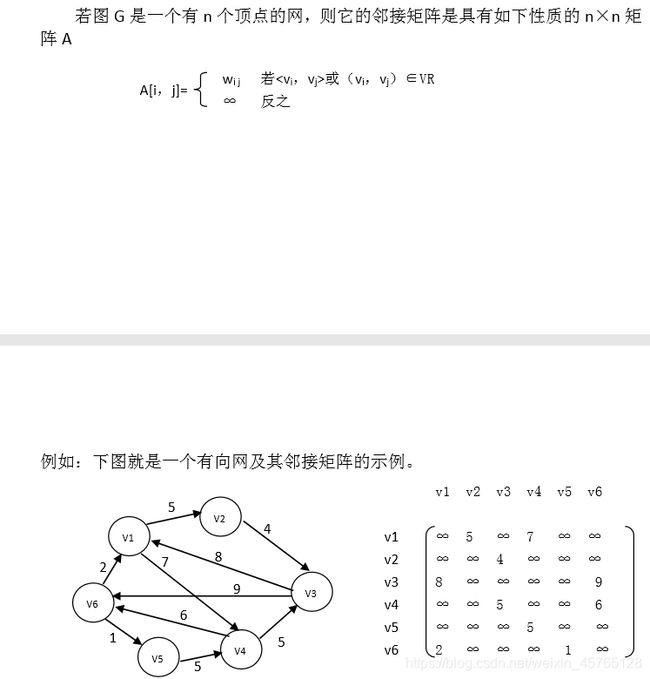
该算法的时间复杂度为 O（n2+e×n），其中 O（n2）时间耗费在对二维数组 arcs 的每个分量的 arj 域初始化赋值上。O（e×n）的时间耗费在有向网中边权的赋值上
| 邻接表表示法 |
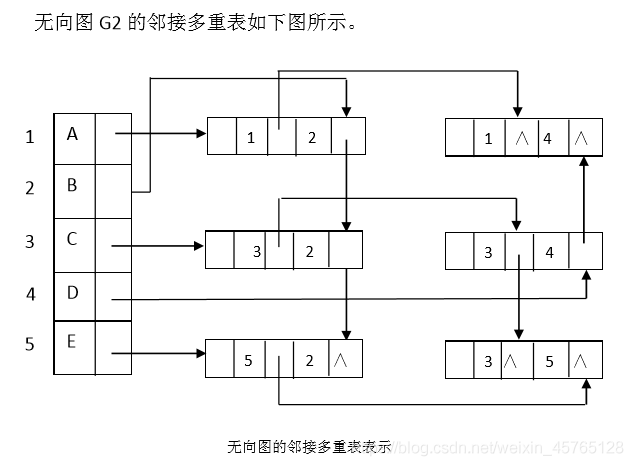
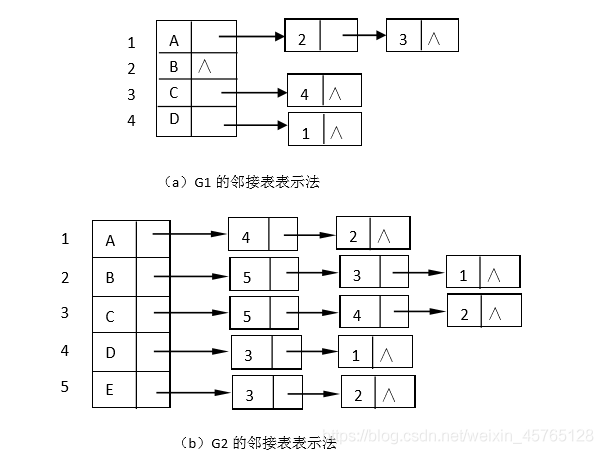
如下图所示分别是图 G1、G2 邻接表表示示例，其中边表中顶点无顺序要求。
| 邻接表存储结构的形式化 |
#define MAX_VERTEX_NUM 20 /*最多顶点个数*/
typedef enum
{
DG,
DN,
UDG,
UDN
} GraphKind; /*图的种类*/
typedef struct ArcNode
{
int adjvex; /*该弧指向顶点的位置*/
struct ArcNode *nextarc; /*指向下一条弧的指针*/
OtherInfo info; /*与该弧相关的信息*/
} ArcNode;
typedef struct VertexNode
{
VertexData data; /*顶点数据*/
ArcNode *firstarc; /*指向该顶点第一条弧的指针*/
} VertexNode;
typedef struct
{
VertexNode vertex[MAX_VERTEX_NUM];
int vexnum, arcnum; /*图的顶点数和弧数*/
GraphKind kind; /*图的种类标志*/
} AdjList; /*基于邻接表的图(Adjacency List Graph)*/
| 十字链表 |
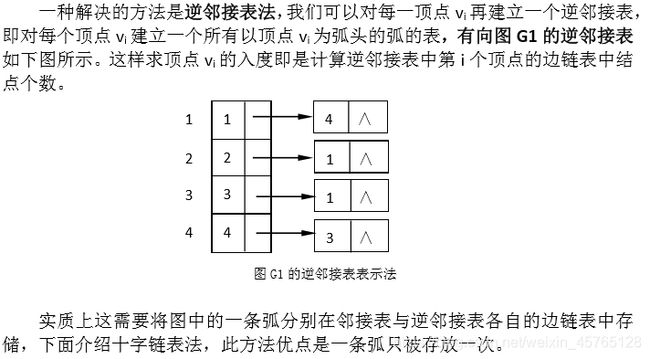
十字链表(Orthogonal List)是有向图的另一种链式存储结构。可以把它看成是将有向图的邻接表和逆邻接表结合起来形成的一种链表。有向图中的每一条弧对应十字链表中的一个弧结点，同时有向图中的每个顶点在十字链表中对应有一个 结点，叫做顶点结点。这两类结点结构如下图所示
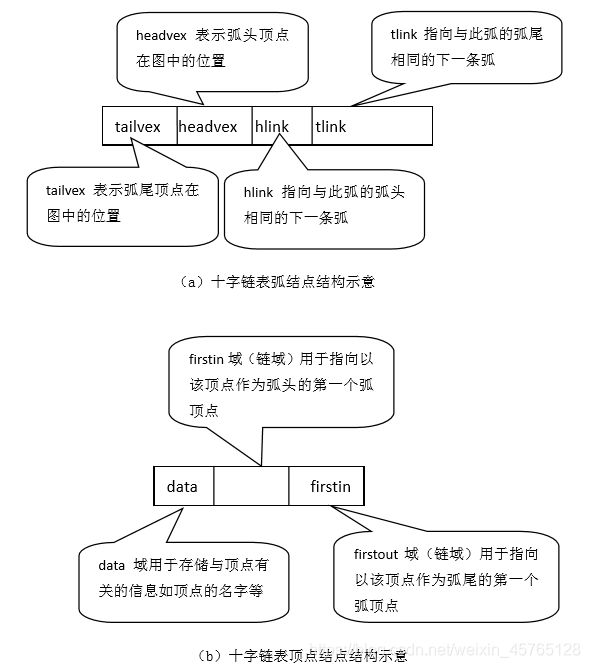
例如：有向图 G1 的十字链表表示如下图所示。若有向图是稀疏图，则它的 邻接矩阵一定是稀疏矩阵，这时该图的十字链表表示法可以看成是其邻接矩阵的 链表表示法。只是在图的十字链表表示法中，弧结点所在的链表不是循环链表且 结点之间相对位置自然形成，不一定按顶点序号有序。另外，表头结点即顶点结 点，它们之间并非循环链式连接，而是顺序存储。
| 十字链表存储结构的形式化 |
#define MAX_VERTEX_NUM 20 /*最多顶点个数*/
typedef enum
{
DG,
DN,
UDG,
UDN
} GraphKind; /*图的种类*/
typedef struct ArcNode
{
int tailvex, headvex;
struct ArcNode *hlink, *tlink;
} ArcNode;
typedef struct VertexNode
{
VertexData data; /*顶点信息*/
ArcNode *firstin, *firstout;
tailvex
} VertexNode;
typedef struct
{
VertexNode vertex[MAX_VERTEX_NUM];
int vexnum, arcnum; /*图的顶点数和弧数*/
GraphKind kind; /*图的种类*/
} OrthList; /*图的十字链表表示法(Orthogonal List)*/
| 建立有向图的十字链表的算法 |
void CrtOrthList（OrthList *g） /*从终端输入 n 个顶点的信息和 e 条弧的信息，以建立一个有向图的十字链表*/
{
scanf(“% d, % d”, &n, &e); /*从键盘输入图的顶点个数和弧的个数*/
g->vexnum = n;
g->arcnum = e;
for (i = 0; i < n; i++)
{
scanf(“% c”, &(g->vertex[i].data));
g->vertex[i].firstin = NULL;
g->vertex[i].firsout = NULL;
}
for (k = 0; k < e; k++)
{
scanf(“% c, % c”, &vt, &vh);
i = LocateVertex（g，vt）;
j = LocateVertex（g，vh）;
p = (ArcNode *)malloc(sizeof(ArcNode));
p->tailvex = I;
p->headvex = j;
p->tlink = g->vertex[i].firstout;
g->vertex[i].firstout = p;
p->hlink = g->vertex[j].firstin;
g->vertex[j].firstin = p;
}
} /* CrtOrthList */
在十字链表中既能够很容易地找到以 vi 为尾的弧，也能够容易地找到以 vi 为头的弧，因此对于有向图，若采用十字链表作为存储结构，则很容易求出顶点 vi的度。此外，为有向图建立一个邻接表的算法和建立一个十字链表的算法的时 间复杂度是相同的。所以，在某些有向图的应用中，十字链表表示法更为合适
| 邻接多重表 |
| 邻接多重表的结构类型说明 |
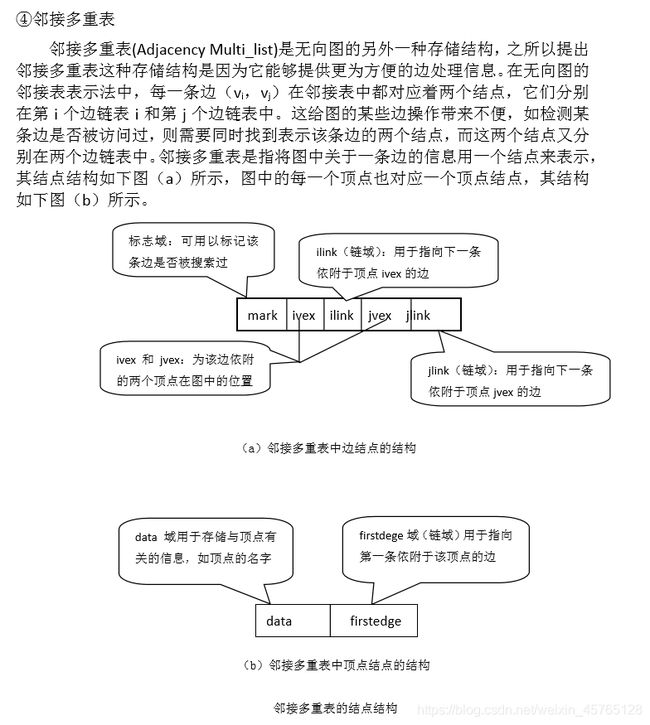
#define MAX_VERTEX_NUM 20 /*最多顶点个数*/
typedef struct EdgeNode
{
int mark, ivex, jvex;
struct EdgeNode *ilink, *jlink;
} EdgeNode;
typedef struct
{
VertexData data;
EdgeNode *firstedge;
} VertexNode;
typedef struct
{
VertexNode vertex[MAX_VERTEX_NUM];
Int vexnum, arcnum; /*图的顶点数和弧数*/
GraphKind kind; /*图的种类*/
} AdjMultiList; /*基于图的邻接多重表表示法(Adjacency Multi_list)*/
