暴力美学2——BFS广度优先搜索

最近在看《算法图解》这本书，我对算法的学习顺序也是根据这本书展开的，这本书上只写了BFS广度优先搜索，没有写BFS深度优先搜索，因此考虑到俩者的关联性，我就先去初步掌握了DFS之后再来学习BFS，有了前面的基础，BFS就相对好掌握很多了。DFS算法和BFS算法都是遍历图的算法，只是它们遍历的方式有所不同，这就会导致在实际应用中它们的应用场景也会有所不同，但其实在很多情况下俩者都是可以相互替换的。其中这篇文章中讲的DFS算法广度优先算法的主要目的是找出最短路径（但不是带权的），

举三个《算法图解》上的例子：

1.编写国际跳棋，计算最少走多少步就可获胜；
2.编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如将READED改为READER需要编辑一个地方；
3.根据你的人际关系网络找到关系最近的医生；

我下面给出一张图，你就可以很清楚地看出BFS算法的基本思想了。

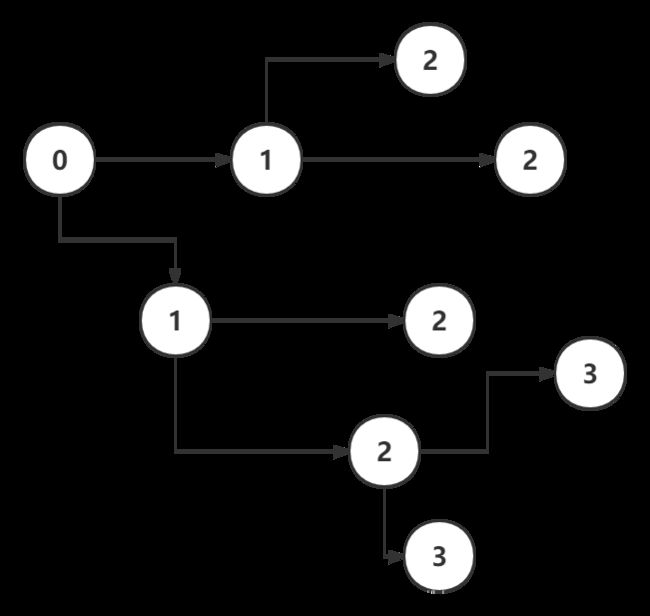
BFS算法的搜索顺序是先搜索初始节点相邻的节点，然后将这次搜索中搜索节点的相邻节点记录下来，等这一轮搜索完后（也就是初始节点相邻的节点搜索完后），再搜索已经记录下来的节点，将这个节点的相邻节点记录下来，等这一轮搜索完后，再搜索记录下来的节点。之后就是不断重复这个过程。 这其实就是队列的实现，队列的工作原理和现实生活中的队列完全相同，队列只支持入队和出队，并且是“先进先出”，“先到先走”，十分公平。BFS算法是将记录的节点直接塞到队列后面，等到前面的节点都搜索完，离开队列后，再开始搜索这些节点，从这个角度看，BFS实际上就是对应队列这个数据结构，而这个数据结构在C++中我们可以通过queue模板实现。

当然，这个算法理解起来虽然比较简单，但是想要用代码实现，还是有点难度，这边我就举两个实际的例子。

第一个例子

Joker先生最近手头没钱了，于是开始着手挖油田（后面程连块），在暴力掠夺了一大堆土地后，他需要你给他统计每一个土地中油田的数量，由于Joker先生过于贪婪，土地简直无法度量，因此人工是无法实现的，需要你通过编程让计算机小朋友去帮你统计。要求：输入一个m行n列（1<=m,n<=100）的字符矩阵，统计字符“@”组成多少个连块。如果两个字符“@”所在的格子相邻（八个方向），就说明他们属于同一个连块。多组输入，当m=0时，输入结束。

如图，就有两个连块

这道题目我之前将其放到了DFS算法的专题里面，实际上这道题目完全可以用BFS来做，因为在这道题目里面，只需要实现搜索的功能就可以了，因此无论是DFS还是BFS都可以实现。

由于本人实在过于懒惰，这边就将大佬的代码贴上去了，我主要是在后面加上了注释，帮助大家理解，因为没有注释去阅读代码实在过于吃力。。。

#include
using namespace std;
const int maxn=105;
int m,n;
int vis[maxn][maxn];
char s[maxn][maxn];
int cnt=0;
int dir[8][2]={
     {
     0,1},{
     1,-1},{
     -1,-1},{
     -1,0},{
     0,-1},{
     -1,1},{
     1,0},{
     1,1}};//用来实现八个方向的遍历
typedef struct Node
{
     
    int x,y;
}node;
void bfs(int x,int y)
{
     
    node p,t;
    queue<node> q; //定义队列
    p.x=x;
    p.y=y;
    q.push(p);	//加入初始节点
    while(!q.empty()) //队列为空就搜索结束
    {
     
        p=q.front(); 
        q.pop();
        for(int i=0;i<8;i++)
        {
     
            t.x=p.x+dir[i][0];
            t.y=p.y+dir[i][1];
            if(t.x<0||t.x>=n||t.x<0||t.y>=m) //搜索条件不满足
            {
     
                continue;
            }
            if(!vis[t.x][t.y]&&s[t.x][t.y]=='@')  //满足搜索条件
            {
     
                vis[t.x][t.y]=1;  //对其进行标记，避免重复搜索
                q.push(t); //添加到队列后面
            }
        }
    }
}
int main()
{
     
    while(scanf("%d %d",&n,&m)&&(n+m))
    {
     
        memset(vis,0,sizeof vis);
        cnt=0;
        for(int i=0;i<n;i++)
        {
     
            scanf("%s",s[i]);
        }
        for(int i=0;i<n;i++)
        {
     
            for(int j=0;j<m;j++)
            {
     
                if(!vis[i][j]&&s[i][j]=='@')
                {
     
                    vis[i][j]=1;
                    cnt++;
                    bfs(i,j);
                }
            }
        }
        printf("%d\n",cnt);
    }
    return 0;
}

可以看出，实际上BFS算法的实现相对DFS还更好理解一点，因为DFS涉及到递归的问题，而BFS算法就是一个很简单的队列的“进入进出”。当然，这只是因为题目相对简单，若是碰到复杂的题目，想要编出正确的BFS算法还是相当有难度的。这边我再给一个例子。

第二个例子

Problem G: 分球

Time Limit: 1 Sec Memory Limit: 64 MB
Submit: 30 Solved: 7

Description

在一个装满财宝的屋子里，有2N个盒子排成一排，除了两个相邻的空盒外，其余的每个盒子里都装有一个金球或银球，总共有N-1个金球和N-1个银球。下面是一个N=5的列子 ，G表示金球，S表示银球。
________________________________________
| G | S | S | G | | | G | S | G | S |
-----------------------------------------
任意2个相邻的非空的盒子里的球可以移动到两个相邻的空盒中，移动不能改变这2个球的顺序。写一个程序，用最小的移动次数把所有的金球都移到所有的银球的左边。

Input

输入包含多组数据。第一行为K,表示数据的总数。 每组数据的第一行是N(3 <= N <=7),第2行是2N个盒子的初始状态。金球用 a表示，银球用b,空盒用空格表示。每2组相邻数据用空行隔开。

Output

对于每一组数据，若无解则输出一行NO SOLUTION,若有解，每行输出移动的步数

Sample Input

3
3
abab

5
abba abab

6
a babbababa

Sample Output

NO SOLUTION
3
4

这道题目是期末考试的压轴题，因为当初没学过搜索算法，所以完全没办法做，最近恰好在研究搜索算法，因此为了弥补一下自己心中的遗憾，就回头做了下这题，确实，这道题目对现在的我而言还是比较难的。。。也是经历了一番波折才将其做出来吧。

这道题目由于是要求最小步，并且设计到搜索，我们可以联想到要使用BFS搜索算法，当然DFS应该也是可以的，不过在这里有可能会超时，最好还是使用BFS算法。

思路大致分成三块：
1.判断当前状态是否符合“左金右银”
2.如何改变小球位置
3.如何对状态进行存储

第一点比较简单，主要通过编写judge函数实现，不过这里有一个细节，就是我一开始把题目意思理解成在空格左边都是金，在空格右边都是银才符合要求，但其实这样是错误的，只要“左金右银就可以了”，中间可以穿插空格，是我想太多了。说到底还是我审题不行。。

第二点的话用string自带的函数就比较容易实现，就是通过substr进行拼接，有了这个函数就相对比较简单了。

第三点是这道题目的关键，我们必须要让步数和当前状态同步存储，这里就需要用到pair模板（当然用结构实现也可以），然后将pair加到队列中就可以了，但是，这个问题还涉及到一个最重要的环节，就是什么时候当前搜索会无法进行下去（注意这里不要和队列为空搞混），这是一个比较难想到的点，其实就是当遇到重复出现的情况的时候，当前搜索就要结束了，开始下一次搜索。而一看到去重，我们就应该可以直接联想到map模板，这个可是去重神器，因此我们将出现过的状态存到map模板里面，就可以很好地实现去重效果。

代码如下

#include
using namespace std;
int judge(string x,int len_x)	//判断是否是“左金右银”状态
{
     
	int i = 0;
	while (x[i]!='b')
	{
     
		i++;
	}
	for (i; i < 2 * len_x; i++)
	{
     
		if (x[i] == 'a') return 0;
	}
	return 1;
}
int bfs(string x,int len_x)	
{
     
	if (judge(x, len_x)) return 0;
	int feet = 0;
	map<string, int> status; //存储搜索过的状态，实现去重效果
	queue<pair<string,int>> q; //定义队列
	pair<string, int> a(x, 0);
	q.push(a); //存入初始状态
	string y;
	int m;
	status[x] = 1;
	while (!q.empty())
	{
     
		y = (q.front()).first;
		m = (q.front()).second;
		q.pop();
		int blank_index;
		if (judge(y, len_x)) //符合"左金右银"，搜索结束，返回搜索次数
		{
     
			return m;
		}
		for (int i = 0; i < y.length() - 1; i++) //查找空格出现的第一个位置，方便后面移动小球
		{
     
			if (y[i] == ' ' && y[i + 1] == ' ')  blank_index = i;
		}
		for (int i = 0; i < y.length() - 1; i++) //开始搜索
		{
     
			if (y[i] != ' ' && y[i + 1] != ' ') //符合搜索条件，交换小球
			{
     
				string z = ""; //z为小球的交换后的状态，下面通过substr拼接算出
				if (blank_index > i)
				{
     
					z = y.substr(0, i) + "  " + y.substr(i + 2, blank_index - i - 2) + y.substr(i, 2) + y.substr(blank_index + 2, 100);
				}
				else
				{
     
					z = y.substr(0, blank_index) + y.substr(i,2)+y.substr(blank_index+2,i-blank_index-2)+"  "+ y.substr(i + 2, 100);
				}
				if (status[z] != 1)  //如果没有存储过这个状态，就将其加到队列后面，并且加入到去重map模板status里面
				{
     
					status[z] = 1;
					pair<string, int> a(z,m+1);
					q.push(a);
				}
			}
		}
	}
	return -1;
}
int main()
{
     
	int N;
	while (cin >> N)
	{
     
		string x;
		int len_x;
		while (N--)
		{
     
			cin >> len_x;
			getchar();
			getline(cin, x);
			int k = bfs(x, len_x);
			if (k == -1)
			{
     
				cout << "NO SOLUTION" << endl;
			}
			else
			{
     
				cout << k<<endl;
			}
		}
	}
}

上述是用BFS实现的，可以看出，如果是一开始接触的话，其实是比较有难度的，在这之后，出于好奇，我又尝试用DFS算法解了下这道题。但很遗憾，我写出来的DFS算法带不动。。。如果有人用DFS做出来了，可以Q我一下，这我确实没有法子。

我的失败代码如下：

#include
using namespace std;
int Min;
int len_x;
map<string, int> status;
int judge(string x)
{
     
	int i = 0;
	while (x[i]!='b')
	{
     
		i++;
	}
	for (i; i < 2 * len_x; i++)
	{
     
		if (x[i] == 'a') return 0;
	}
	return 1;
}
void dfs(string x,int n)
{
     
	if (judge(x))
	{
     
		if (Min == -1)
		{
     
			Min = n;
			return;
		}
		else
		{
     
			if (n < Min) Min = n;
			return;
		}
	}
	int blank_index;
	for (int i = 0; i < x.length() - 1; i++) //查找空格出现的第一个位置，方便后面移动小球
	{
     
		if (x[i] == ' ' && x[i + 1] == ' ')  blank_index = i;
	}
	for (int i = 0; i < x.length() - 1; i++) //开始搜索
	{
     
		if (x[i] != ' ' && x[i + 1] != ' ') //符合搜索条件，交换小球
		{
     
			string z = ""; //z为小球的交换后的状态，下面通过substr拼接算出
			if (blank_index > i)
			{
     
				z = x.substr(0, i) + "  " + x.substr(i + 2, blank_index - i - 2) + x.substr(i, 2) + x.substr(blank_index + 2, 100);
			}
			else
			{
     
				z = x.substr(0, blank_index) + x.substr(i, 2) + x.substr(blank_index + 2, i - blank_index - 2) + "  " + x.substr(i + 2, 100);
			}
			if (status[z] != 1)
			{
     
				status[z] = 1;
				dfs(z, n + 1);
				status[z] = 0;
			}
		}

	}
}
int main()
{
     
	int N;
	while (cin >> N)
	{
     
		string x;
		while (N--)
		{
     
			Min = -1;
			cin >> len_x;
			getchar();
			getline(cin, x);
			if (judge(x))
			{
     
				cout << 0 << endl;
			}
			else
			{
     
				status[x] = 1;
				dfs(x, 0);
				if (Min == -1)
				{
     
					cout << "NO SOLUTION" << endl;
				}
				else
				{
     
					cout << Min << endl;
				}
			}
		}
	}
}

如果觉得有帮助，可以关注一下我的公众号，我的公众号主要是将这些文章进行美化加工，以更加精美的方式展现出来，同时记录我大学四年的生活，谢谢你们！