2---理解正余弦、复数求模、反正切和乘除运算的CORDIC算法实现

CORDIC（Coordinate Rotation Digital Computer）算法是J.Volder在1956在航空控制系统设计中构思的，但其实相似的算法在更早的1624年就已经被Henry Briggs公布了。https://en.wikipedia.org/wiki/CORDIC
CORDIC的基本思想： 通过坐标旋转不断的迭代，去逼近一个设定的值，其核心是每次迭代旋转的角度是上一次的一半（类似于2分法），这样计算可通过加法和移位实现，适合数字电路实现。
CORDIC能实现的计算： 乘、除、平方根、正弦、余弦、反正切、复数乘法、坐标转换、指数运算等
CORDIC算法原理参考链接：
Xilinx CORDIC算法
三角函数计算，Cordic 算法入门

1. 圆周旋转，计算正余弦、复数求模、反正切

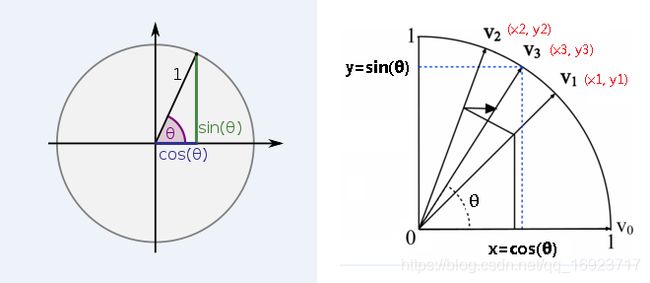
先看下边第一个图，圆周旋转其实就是对圆坐标系上的点进行旋转，从图中可以看到3个参数，坐标参数（x，y）和角度值$\theta$，如果圆的半径$R=1$，则有

$x=\cos \theta$
$y=\sin \theta$
$R=\sqrt{x^2+y^2}=\sqrt{{\cos }^2\theta +{\sin }^2\theta }=1$

那么如果我们知道角度为$\theta$时的坐标参数$(x,y)$，我们就能知道$\theta$的正余弦函数值

$\cos \theta =x$
$\sin \theta =y$

那么怎么获得这个坐标参数呢，请看下边第二个图，我们想要计算的角度值为$\theta$，其对应的坐标值为$(x_3,y_3)$，我们通过旋转来不断的逼近这个坐标点$V_3$，每次旋转的角度都是固定的，并且越来越小。如果旋转超过了$V_3$，如$V_1$到$V_2$的旋转，则下次旋转的方向与之前相反。就这样不断的在$V_3$附近摆动，因为旋转的角度不断减小，所以会越来越接近$V_3$。这个在目标值附近不断摆动并接近目标值的过程就是迭代。

迭代需要注意的细节有

• 半径R的伸缩
• 每次迭代要旋转的固定角度

这里会涉及到几个公式如下，公式详细可参考Xilinx CORDIC算法

$x_{i+1}=x_i-d_i(y_i{2}^{-i})$
$y_{i+1}=y_i+d_i(x_i{2}^{-i})$
$z_{i+1}=z_i-d_i{\theta }_i$

$i$是迭代次数，$d_i$是判断算子，用来确定旋转的方向，$z$是角度累加器。

怎么计算正余弦

计算正余弦就是要计算坐标值，此时我们已经知道了角度值$z$，计算正余弦的过程如下

• 设定初始的坐标为(1, 0)
• 旋转$z$个角度，即使$z$趋于0
• 最终得到的$x$和$y$的值就是我们要的正余弦函数值

可通过下面这段MATLAB代码来理解

for i = 0:1:itime					% itime为迭代次数
   if z0 > 0                        % z0生成判断算子，确定旋转方向
       x = x0 - y0 / 2^(i);
       y = y0 + x0 / 2^(i);
       z = z0 - atan(1/2^i);
   else
       x = x0 + y0 / 2^(i);
       y = y0 - x0 / 2^(i);
       z = z0 + atan(1/2^i);
   end
   x0 = x;
   y0 = y;
   z0 = z;
end

怎么计算复数求模和反正切

先看我们要求的是什么

$|a+bi|=\sqrt{(a{)}^2+(b{)}^2}=\sqrt{(\sqrt{(a{)}^2+(b{)}^2}{)}^2+(0{)}^2}$
$ta{n}^{-1}(a)=ta{n}^{-1}(\frac{a}{1})=ta{n}^{-1}(\frac{y}{x})=\theta$
其中$y=a$，$x=1$

计算正余弦函数的过程可以看成是第二图中$V_0$到$V_3$的旋转，而计算复数求模和反正切就可以看成是**$V_3$到$V_0$的旋转**，即初始我们是知道$(x_3,y_3)$的，然后我们要求$(x_0,0)$的值，因为这是圆周旋转，所以这里有一个隐含条件

$\sqrt{(x_3{)}^2+(y_3{)}^2}=\sqrt{(x_0{)}^2+(0{)}^2}=|x_0|$

那么复数求模$a+bi$的过程如下

• 设定初始值$x_0=a,y_0=b,z_0=0$。如果只求模，$z$其实无所谓，因为求解过程不需要用到$z$
• 使$y$趋于0
• 迭代完成后的结果$x$就是复数的模

求反正切的过程与复数求模基本一致，因为都是$V_3$到$V_0$的旋转，在这个迭代过程中，$z$一直在积累角度，迭代完成后**$z$的值就是旋转的角度$\theta$**。即有

$\theta =ta{n}^{-1}(\frac{b}{a})$

如果我们将初始值$y$设为$x=a=1$，那么$b$的反正切函数值为

$ta{n}^{-1}(b)=z=\theta$

计算复数求模和反正切函数值的MATLAB代码

for i = 0:1:itime					% itime为迭代次数，迭代的越多，越精确
   if y0 < 0                        % y0生成判断算子，确定旋转方向
       x = x0 - y0 / 2^(i);
       y = y0 + x0 / 2^(i);
       z = z0 - atan(1/2^i);
   else
       x = x0 + y0 / 2^(i);
       y = y0 - x0 / 2^(i);
       z = z0 + atan(1/2^i);
   end
   x0 = x;
   y0 = y;
   z0 = z;
end

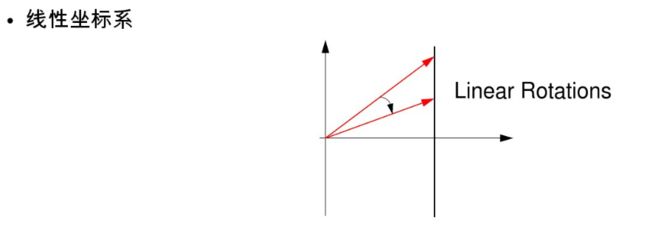
2. 线性旋转，乘除运算的CORDIC实现

Xilinx CORDIC算法在介绍线性旋转的时候有说到一个线性坐标系，有的讲CORDIC的书里也有提到线性坐标系旋转，但是也有的书里是没有提到的，而且在百度和谷歌里都没搜到“线性坐标系”这个名词，所以也不知道是不是对的。不过从下面这个图来理解线性旋转好像确实有点不好理解，所以就先不管了。

• 线性旋转的迭代过程可表示为

$x_{i+1}=x_i$
$y_{i+1}=y_i+d_i(x_i{2}^{-i})$
$z_{i+1}=z_i-d_i(2^{-i})$

• 选择$d_i=sign(z_i)$使得$z_i\to 0$。$n$次迭代后得到

$x_n=x_0$
$y_n=y_0+x_0{z}_0$
$z_n=0$

如果初始$y_0$设为0，那么迭代完成后就可以得到$x$与$z$的乘积。

• 选择$d_i=-sign(x_i{y}_i)$使得$y_i\to 0$。$n$次迭代后得到

$x_n=x_0$
$y_n=0$
$z_n=z_0+\frac{y_0}{x_0}$

如果初始$z_0$设为0，那么迭代完成后就可以得到$y$除$x$的商。

其实上面的过程隐含了一个等式

$y=xz$

我们都知道乘法可以通过二进制的移位相加来实现，如6乘以5

$5=2^2+2^0$
则 6乘5 = 6左移2位 + 6
6*5 = 0b(11000) + 0b(00110) = 0b(11110) = 30

所以求乘积的过程就是$x_0$不断移位相加的过程，这个过程会近似乘完所有$z_0$的分解项（分解成如$5=2^2+2^0$的形式），每次乘积后累加，最后得到$y^n$。
而求商的过程则与求乘积的过程恰好相反

乘法迭代的MATLAB代码

for i = -indx:15			% 注意indx				
   if z0 > 0                       
       x = x0;
       y = y0 + x0 / 2^(i);
       z = z0 - (1/2^i);
   else
       x = x0;
       y = y0 - x0 / 2^(i);
       z = z0 + (1/2^i);
   end
   x0 = x;
   y0 = y;
   z0 = z;
end

注意$2^{indx}$必须大于$z_0$的$\frac{1}{2}$，否则迭代不会收敛，即$z$不会趋于0

除法迭代的MATLAB代码

for i = -indx:15					
   if y0 < 0                       
       x = x0;
       y = y0 + x0 / 2^(i);
       z = z0 - (1/2^i);
   else
       x = x0;
       y = y0 - x0 / 2^(i);
       z = z0 + (1/2^i);
   end
   x0 = x;
   y0 = y;
   z0 = z;
fprintf('x0 = %d, y0 = %d, z0 = %d\n', x0, y0, z0)
end

注意$x_0\ast 2^{indx}$必须大于$y_0$的$\frac{1}{2}$，否则迭代不会收敛，即$y$不会趋于0

为什么不会收敛呢
因为”一尺之棰，日取其半，万世不竭”…………
拿乘法来说，假设$z_0=100$， $indx=5$，那迭代$n$次之后有

$z_n=z_0-(2^5+2^4+...+2^{5-n+1})=100-2^6(1-2^{-n})=36+2^{6-n}$

即不管迭代多少次，$z_n$是永远大于36的，所以不能收敛。