LeetCode学习笔记——打家劫舍系列(动态规划)
个人博客:The Blog Of WaiterXiaoYY 欢迎来互相交流学习。
今天,继续记录动态规划。
相比于前两天对动态规划的理解,今天对动态规划的理解也可以说更进一步了,
但离真正的掌握,运用于股掌之中还有很长的距离。
总结:解决动态规划问题,就是要找状态和选择。
我之前理解动态规划是在递归的过程中记录重复的值,其实这只是一种,可以说只是用动态规划来优化,
解决动态规划问题的本质,就是找出对象的状态,然后写出状态转移方程。
先看一道打家劫舍的问题,
打家劫舍 I
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
解题思路
题目很好理解,也就是说如果你(没错,你先假装小偷)进入了第一间房子,
现在的智能(人工)检测,你不能进入第二间房子,否则就凉凉,
那你只能走到第三间房子了,这时候可以有两种选择:进入或者不进入。
也就是说,对每一间房子,你都有两种选择,
而选择的依据是你进入后偷的钱能否最大化。
所以我们就总结出了状态和选择,
房子的索引就是状态,进入和不进入就是选择。
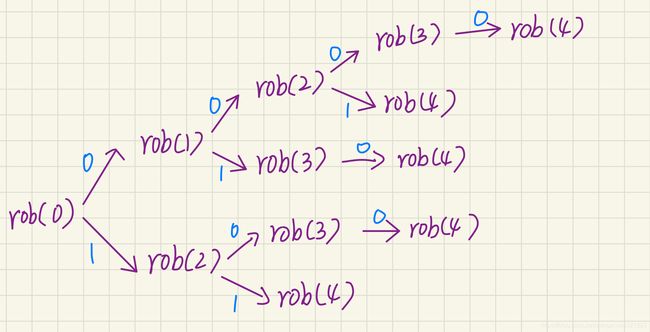
这时候我们需要转为状态方程,我们先模拟一下:
假设有五间间房子,从第一间开始就可以做选择,下面就是全部状态(0-不进去;1-进入),只需要把每一种情况的值求出来,再求他们的最大值,就是我们想要的结果。
可以看出来,这个跟我们的递归一样,里面有很多重复的情况,
比如 rob(3),rob(3)的两种选择在上面的模拟过程中重复了很多次,
我们需要有个东西来记录着我们每次选择的值,这样子就不需要重复运算。
我们先将上面的模拟过程转为状态方程:
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])
这个dp数组记录的就是选择本次,并且选择了前前一次,如果前前一次加上本次的值大于上一个记录的值,就保存新的值下来,否则维持之前的值。
有点抽象?
确实,我觉得动态规划就是难在这里。
有时候觉得明白了是一瞬间的事情,但过后会忘,或者难以言表,这都是没有真正掌握的缘故。
我们看一下下面的推演:
| 编号 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 价值 | 1 | 2 | 3 | 1 |
| dp[i] | 1 | 2 | 4 | 4 |
有点眉目没?
dp[0],也就是在第一间房子的时候,假设进入了,则现在能获得的最大值是1,
dp[1],到了第二间房子,进入了第一间房子,当然就不能进入第二间了,但是进第一间没有进入第二间的价值大,那我当然选择进入第二间,就更新值为2,
dp[2],到了第三间房子,进不进呢?得看前两间的选择,如果进入了第二间房子,当然就不能进第三间,那这时候的价值依旧只是2,但如果我不进第二间,而是进第一间,然后这时候我就可以进第三间了,那价值就变成了4,
第四间同理。
如果明白了这个,那我们的代码就出来了。
代码
class Solution {
public int rob(int[] nums) {
//判断特殊情况
if (nums.length <= 1) return nums.length == 0 ? 0 : nums[0];
int []dp = new int[nums.length];
//初始值
dp[0] = nums[0];
dp[1] = Math.max(dp[0], nums[1]);
//从第三间开始记录值
for(int i = 2; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
//dp数组最后一个值为最大价值
return dp[nums.length - 1];
}
}
呼……放松一下,准备进入我们的第二题……
打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [2,3,2]
输出: 3
解释: 你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入: [1,2,3,1]
输出: 4
解释: 你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
解题思路
这道题相比于第一题的不同点在于,你今天偷的客家土楼,是房子是围着一圈的,
也就是说不能同时进入第一间房子和最后一间房子,
那就可以分为三种情况:
- 进第一间,不进最后一间
- 不进第一间,进最后一间
- 两间都不进
那我们是不是要三种情况都需要进入讨论,不是的,我们只需要讨论前两种,
因为前两种的选择范围都包括了第三种。
那这个问题就可以转换成两个问题来解决,
- 从第二间到第n间
- 从第一间到第n - 1间
只要求出这种情况的最大值就行,而每种情况,都是可以说是第一题,
不过需要注意的是,并不是缩短nums数组的长度,而是将我们已知道不需要考虑的情况初始化,
结合第一题的思路,我们就可以写出我们的代码了。
代码
class Solution {
public int rob(int[] nums) {
if(nums.length == 0) return 0;
if(nums.length == 1) return nums[0];
int []res1 = new int[nums.length];
int []res2 = new int[nums.length];
//第一种情况从第二间到第n间
res1[0] = 0;
res1[1] = nums[1];
//第二种情况是从第一间到第n - 1间
res2[0] = nums[0];
res2[1] = Math.max(nums[0], nums[1]);
for(int i = 2; i < nums.length; i++) {
res1[i] = Math.max(res1[i - 1], res1[i - 2] + nums[i]);
}
for(int i = 2; i < nums.length; i++) {
res2[i] = Math.max(res2[i - 1], res2[i - 2] + nums[i]);
}
//返回两种情况的最大值
return Math.max(res1[nums.length - 1], res2[nums.length - 2]);
}
}
打家劫舍 III
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
示例 1:
输入: [3,2,3,null,3,null,1]
3
/ \
2 3
\ \
3 1
输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
示例 2:
输入: [3,4,5,1,3,null,1]
3
/ \
4 5
/ \ \
1 3 1
输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.
解题思路
终于来到最后一题了,这小偷开始不知道偷哪里的房子了。
其实这道题也是万变不离其宗,
虽然他是树,但是他每一个结点都有选择的情况,
选择了爷爷结点,自然不能选儿子结点了,得去到孙子结点那里做选择,
不过树给我的感觉就是,一看到树,八成会用到递归,
这道题也确实应该用递归。
我们再来分析一下题,
每个结点都有选和不选的情况,
假设我们在选择根结点root,
那我们只能从root的左右子树的左右子树中去选择了,
那如果不选择根节点root,
那就从root的左右子树中去选择。
一开始我是这样做的:
class Solution {
public int rob(TreeNode root) {
if(root == null)
return 0;
//选择结点root
int res1 = root.val;
//对root的的左右子树的左右子树进行选择
if(root.left != null)
res1 += rob(root.left.left) + rob(root.left.right);
if(root.right != null)
res1 += rob(root.right.left) + rob(root.right.right);
//不选择root的情况
int res2 = rob(root.left) + rob(root.right);
//返回两种情况的最大值
return Math.max(res2, res1);
}
}
成功通过,但是时间复杂度很大,因为我们进行了多次重复计算,
所以我们可以申请一个备忘录记录我们遍历过的值,
经过改进后,代码如下:
代码
class Solution {
//申请一个哈希表作为备忘录
Map<TreeNode, Integer> memo = new HashMap<>();
public int rob(TreeNode root) {
if(root == null)
return 0;
//如果备忘录中有root作为起始点的值了,就返回
if(memo.containsKey(root))
return memo.get(root);
//选择结点root
int res1 = root.val;
//对root的的左右子树的左右子树进行选择
if(root.left != null)
res1 += rob(root.left.left) + rob(root.left.right);
if(root.right != null)
res1 += rob(root.right.left) + rob(root.right.right);
//不选择root的情况
int res2 = rob(root.left) + rob(root.right);
//返回两种情况的最大值
int res = Math.max(res2, res1);
//记录到备忘录里面
memo.put(root, res);
return res;
}
}
这里记录一下我对递归看法,递归是个很好用的工具,很多难以解决的问题都可以丢给递归去运算,因为递归不会累,但是就很容易出现重复运算和错误,而错误又是很难找出来的,甚至还需Debug,所以递归好用,但勿滥用。
整理于2020.3.21