图匹配

二分图：

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

简单的说，一个图被分成了两部分，相同的部分没有边，那这个图就是二分图，二分图是特殊的图。

匹配：

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。

最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。

如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。
求二分图匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)

注意匈牙利算法，除了二分图多重匹配外在二分图匹配中都可以使用。

注：二分图匹配中还有一个hk算法，复杂度为o（sqrt（n）*e）由于复杂度降低较低，代码量飙升而且绝大多数情况下没人会闲的卡个sqrt的复杂度。。在此先不讲了，有兴趣可以自己百度，貌似卡这个算法的只有hdu2389

匈牙利算法：

匈牙利算法几乎是二分图匹配的核心算法，除了二分图多重匹配外均可使用

匈牙利算法实际上就是一种网络流的思想，其核心就是寻找增广路。具体操作就是嗯。。拉郎配

 

注：以下转自 http://blog.csdn.net/dark_scope/article/details/8880547

匈牙利算法是由匈牙利数学家Edmonds于1965年提出，因而得名。匈牙利算法是基于Hall定理中充分性证明的思想，它是部图匹配最常见的算法，该算法的核心就是寻找增广路径，它是一种用增广路径求二分图最大匹配的算法。

-------等等，看得头大？那么请看下面的版本：

 

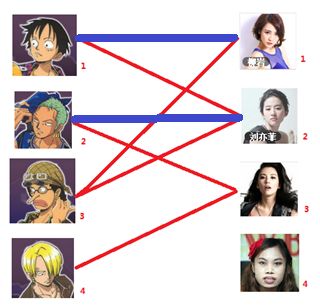
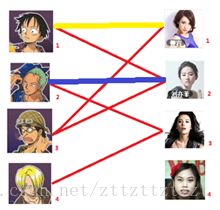
通过数代人的努力，你终于赶上了剩男剩女的大潮，假设你是一位光荣的新世纪媒人，在你的手上有N个剩男，M个剩女，每个人都可能对多名异性有好感（-_-||暂时不考虑特殊的性取向），如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在让我们无视掉所有的单相思（好忧伤的感觉），你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

 

一： 先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，got it，连上一条蓝线

二：接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，got it

三：接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？

我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。

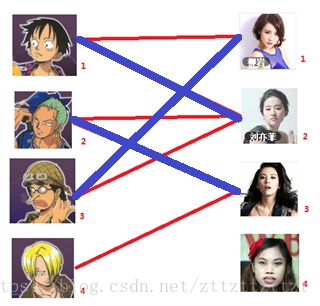
与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配()重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

那么第三部结果就是

 

代码中最重要的就是递归了

ac代码

#include 
#include
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
const int N = 505;
struct  po
{
	int id,high;
	char sex[10],sport[100],music[100];
}p[N];// 学生 
int t,n;
int ret;// 最大匹配数 
int g[N][N];//建双向遍 
int used[N];  //标记 正在匹配的男同学 的 可匹配的女同学 是否已匹配 
int match[N];  //标记i的匹配 u  
//bool dfs(int u)  
//{  
//    for(int i=1;i<=vN;i++)  
//    {  
//        if(!used[i] && g[u][i])  
//        {  
//            used[i] = true;  
//            if(match[i] == -1 || dfs(match[i]))  
//            {  
//                match[i] = u;  
//                return true;  
//            }  
//        }  
//    }  
//    return false;  
//}  
bool dfs(int u)  //递归 匹配 
{
	for(int i=1;i<=n;i++)
	{
		if(!used[i]&&g[u][i])
		{
			used[i]=true;
			if(match[i]==-1||dfs(match[i]))// 如果i 未匹配，或者可以找到其他匹配的话，就让 u与i匹配 
			{
				match[i]=u;
				return true;
			}
		}
	}
	return false;
}
bool check(int i,int j)//检查是否可以匹配 
{
	if(strcmp(p[i].sex,p[j].sex)==0)  return false;
	
	if(abs(p[i].high - p[j].high) > 40) return false;  
    //身高差超过40cm
    if (strcmp(p[i].music, p[j].music)) return false;
    //喜欢的音乐类型相同
    if (!strcmp(p[i].sport, p[j].sport)) return false;
    //喜欢的体育类型不同
    return true;  
}
void init()//初始化 
{
	memset(g,0,sizeof(g));
	memset(match,-1,sizeof(match));
}
int hungary()  // 记录ret 也就是匹配数 
{  
    int ret = 0;  
    for(int i=1;i<=n;i++)     
    {  
        memset(used,0,sizeof(used));  
        if(p[i].sex[0]=='M'&&dfs(i))  ret++;  
    }  
    return ret;
}
int main()
{
	cin>>t;
	while(t--)
	{
		cin>>n;
		init();
		for(int i=1;i<=n;i++)
		{
			cin>>p[i].high>>p[i].sex >>p[i].music >>p[i].sport ;
			p[i].id=i;
		}
		for(int i=1;i<=n;i++)
		{
			for(int j = 1; j <= n; j++) 
            //将可以匹配的男女建边
            if(check(i,j)) 
			g[i][j] = g[j][i] = 1;  // 建立匹配边 
        }
        	cout<

 

本来不想摘抄的，可是他们的代码都没有注释，唉