R语言实现 预测数值型数据——回归方法（线性回归、回归树、模型树）

Example: Predicting Medical Expenses

Part 1: Linear Regression

Step 1: Exploring and preparing the data ----

insurance <- read.csv("F:\\rwork\\Machine Learning with R (2nd Ed.)\\Chapter 06\\insurance.csv", stringsAsFactors = TRUE)
str(insurance)

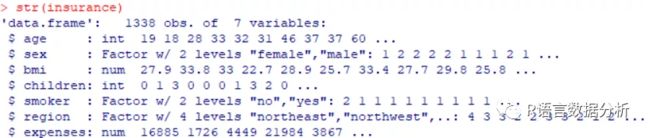
summarize the charges variable

summary(insurance$expenses)

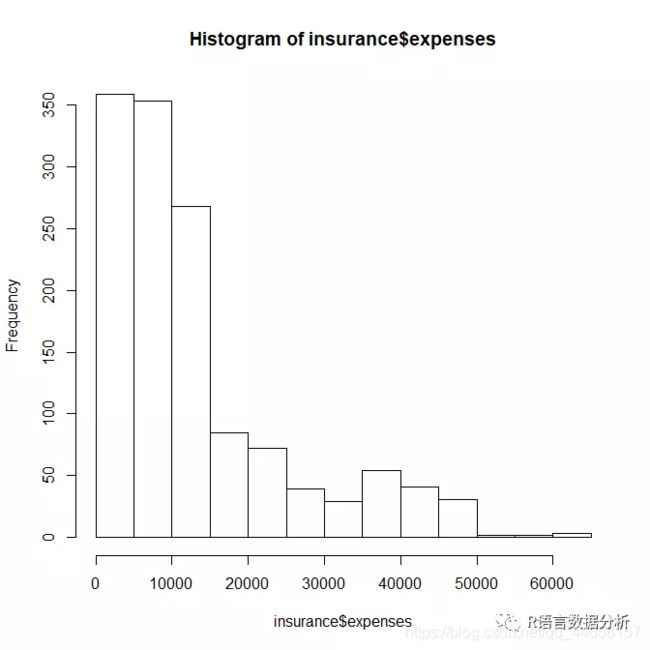
histogram of insurance charges

hist(insurance$expenses)

table of region

table(insurance$region)

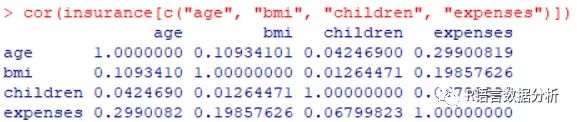
exploring relationships among features: correlation matrix

cor(insurance[c("age", "bmi", "children", "expenses")])

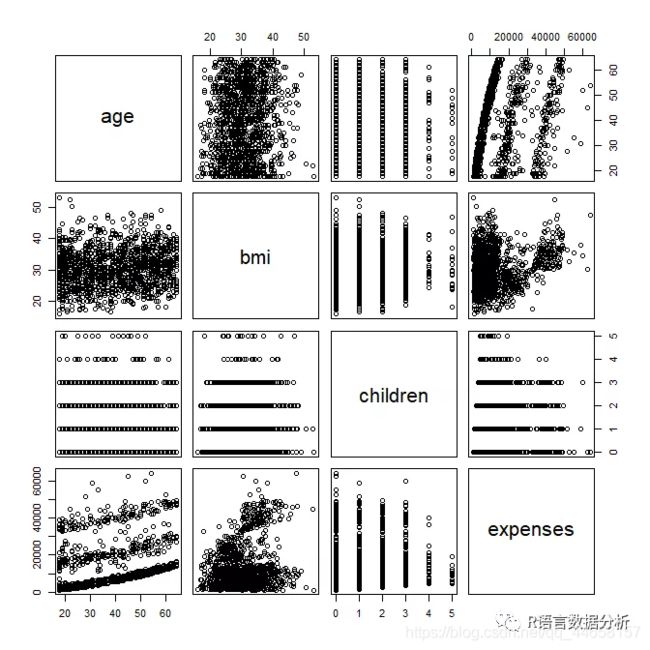
visualing relationships among features: scatterplot matrix

pairs(insurance[c("age", "bmi", "children", "expenses")])

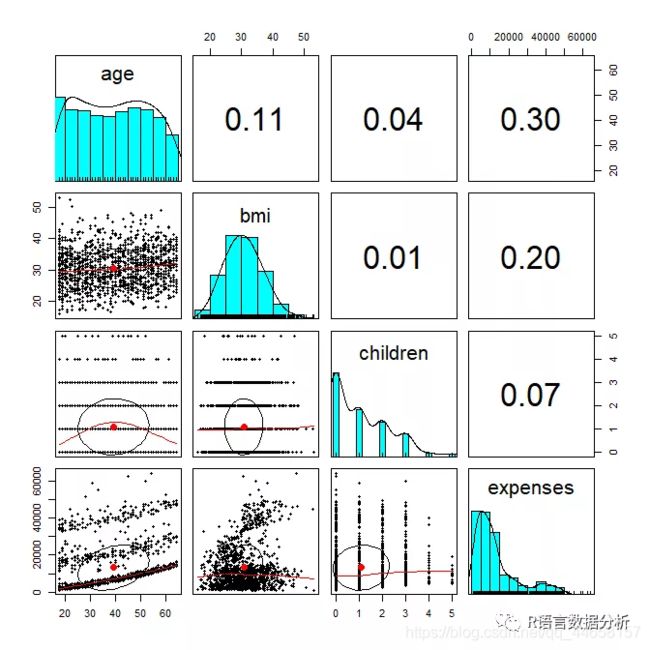
more informative scatterplot matrix

#install.packages('psych')
library(psych)
pairs.panels(insurance[c("age", "bmi", "children", "expenses")])

Step 2: Training a model on the data ----

ins_model <- lm(expenses ~ ., data = insurance)

see the estimated beta coefficients

ins_model

Step 3: Evaluating model performance ----

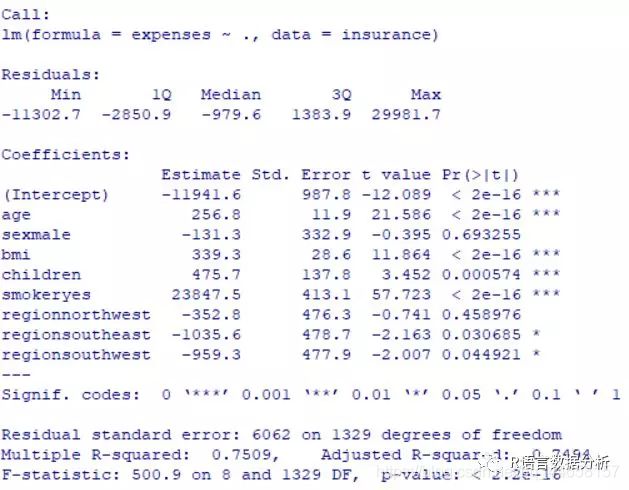
see more detail about the estimated beta coefficients

summary(ins_model)

Step 4: Improving model performance ----

add a higher-order “age” term

insurance$age2 <- insurance$age^2

add an indicator for BMI >= 30

insurance$bmi30 <- ifelse(insurance$bmi >= 30, 1, 0)

create final model

ins_model2 <- lm(expenses ~ age + age2 + children + bmi + sex +
                   bmi30*smoker + region, data = insurance)
                   
summary(ins_model2)

Example: Estimating Wine Quality ----

Part 2: Regression Trees and Model Trees

Step 1: Exploring and preparing the data ----

wine <- read.csv("F:\\rwork\\Machine Learning with R (2nd Ed.)\\Chapter 06\\whitewines.csv")

examine the wine data

str(wine)

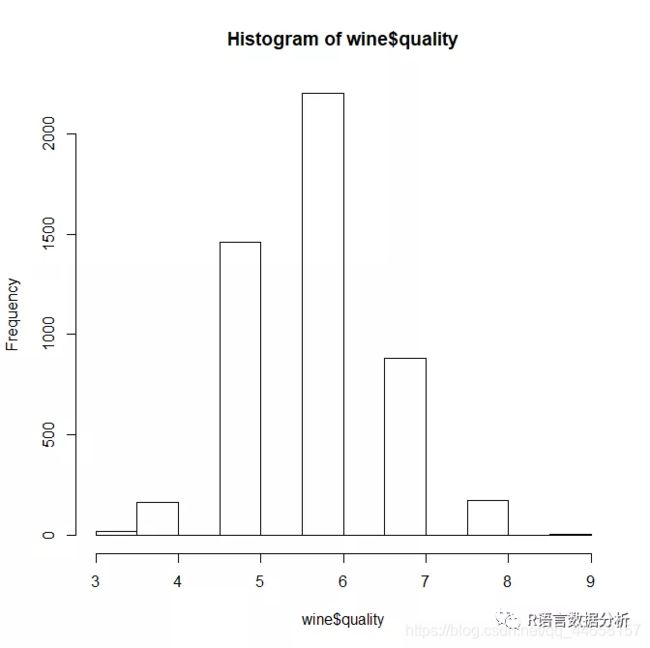
the distribution of quality ratings

hist(wine$quality)

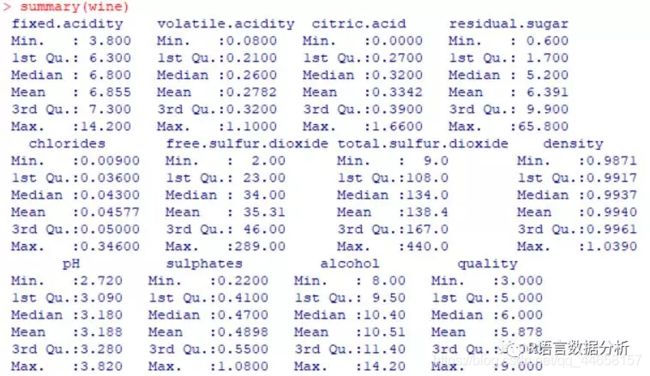
summary statistics of the wine data

summary(wine)

wine_train <- wine[1:3750, ]
wine_test <- wine[3751:4898, ]

Step 2: Training a model on the data ----

regression tree using rpart

library(rpart)
m.rpart <- rpart(quality ~ ., data = wine_train)

get basic information about the tree

m.rpart

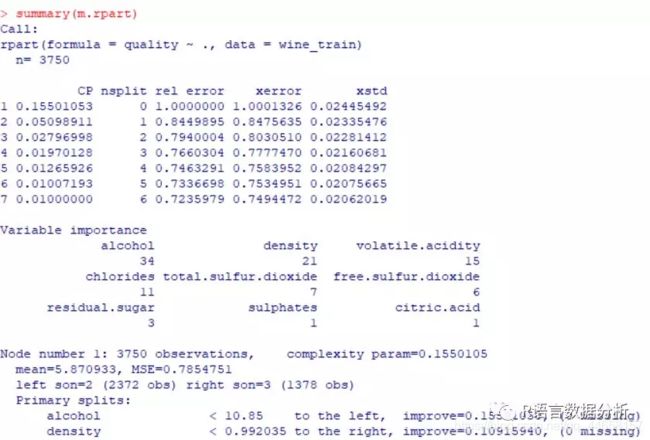
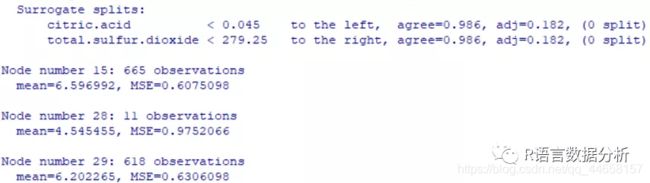
get more detailed information about the tree

summary(m.rpart)

use the rpart.plot package to create a visualization

#install.packages('rpart.plot')
library(rpart.plot)

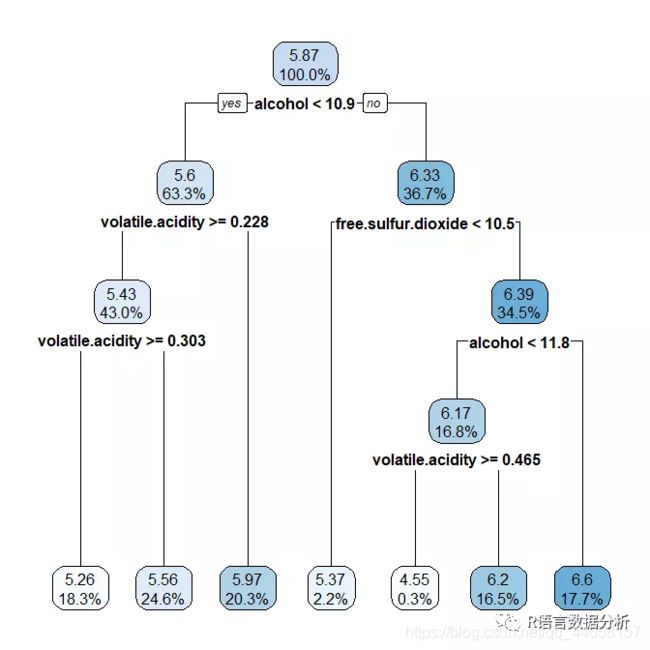
a basic decision tree diagram

rpart.plot(m.rpart, digits = 3)

a few adjustments to the diagram

rpart.plot(m.rpart, digits = 4, fallen.leaves = TRUE, type = 3, extra = 101)

Step 3: Evaluate model performance ----

generate predictions for the testing dataset

p.rpart <- predict(m.rpart, wine_test)

compare the distribution of predicted values vs. actual values

summary(p.rpart)
summary(wine_test$quality)

compare the correlation

cor(p.rpart, wine_test$quality)

function to calculate the mean absolute error

MAE <- function(actual, predicted) {
  mean(abs(actual - predicted))  }

mean absolute error between predicted and actual values

MAE(p.rpart, wine_test$quality)

mean absolute error between actual values and mean value

mean(wine_train$quality) # result = 5.87
MAE(5.87, wine_test$quality)

Step 4: Improving model performance ----

train a M5’ Model Tree

library(RWeka)
m.m5p <- M5P(quality ~ ., data = wine_train)

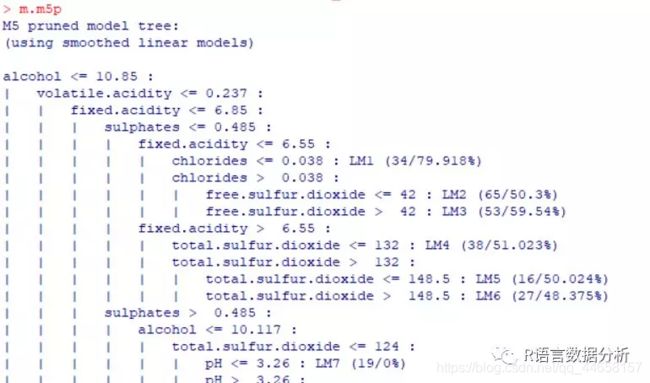
display the tree

m.m5p

​（信息过长，有163种情况，这里就不全部截图了）

get a summary of the model’s performance

summary(m.m5p)

generate predictions for the model

p.m5p <- predict(m.m5p, wine_test)

summary statistics about the predictions

summary(p.m5p)

correlation between the predicted and true values

cor(p.m5p, wine_test$quality)

mean absolute error of predicted and true values
(uses a custom function defined above)

MAE(wine_test$quality, p.m5p)

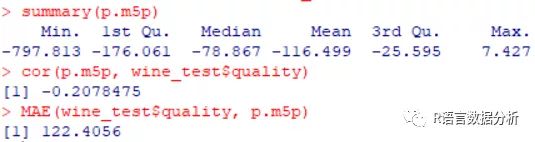
​这里就得出了一个很奇怪的结论，因为一般来说使用先进的M5算法后模型的准确度会得到提高，即平均绝对误差（MAE）会减小，但是这次不减反增。大家可以自己选择数据试试，有问题留言哦~