CCFCSP 201612-4 压缩编码(100score)

题目来源于CCFCSP

---

问题描述

给定一段文字，已知单词a1, a2, …, an出现的频率分别t1, t2, …, tn。可以用01串给这些单词编码，即将每个单词与一个01串对应，使得任何一个单词的编码（对应的01串）不是另一个单词编码的前缀，这种编码称为前缀码。
　　使用前缀码编码一段文字是指将这段文字中的每个单词依次对应到其编码。一段文字经过前缀编码后的长度为：
　　L=a1的编码长度×t1+a2的编码长度×t2+…+ an的编码长度×tn。
　　定义一个前缀编码为字典序编码，指对于1 ≤ i < n，ai的编码（对应的01串）的字典序在ai+1编码之前，即a1, a2, …, an的编码是按字典序升序排列的。
　　例如，文字E A E C D E B C C E C B D B E中， 5个单词A、B、C、D、E出现的频率分别为1, 3, 4, 2, 5，则一种可行的编码方案是A:000, B:001, C:01, D:10, E:11，对应的编码后的01串为1100011011011001010111010011000111，对应的长度L为3×1+3×3+2×4+2×2+2×5=34。
　　在这个例子中，如果使用哈夫曼(Huffman)编码，对应的编码方案是A:000, B:01, C:10, D:001, E:11，虽然最终文字编码后的总长度只有33，但是这个编码不满足字典序编码的性质，比如C的编码的字典序不在D的编码之前。
　　在这个例子中，有些人可能会想的另一个字典序编码是A:000, B:001, C:010, D:011, E:1，编码后的文字长度为35。
　　请找出一个字典序编码，使得文字经过编码后的长度L最小。在输出时，你只需要输出最小的长度L，而不需要输出具体的方案。在上面的例子中，最小的长度L为34。

输入格式

输入的第一行包含一个整数n，表示单词的数量。
　　第二行包含n个整数，用空格分隔，分别表示a1, a2, …, an出现的频率，即t1, t2, …, tn。请注意a1, a2, …, an具体是什么单词并不影响本题的解，所以没有输入a1, a2, …, an。

输出格式

输出一个整数，表示文字经过编码后的长度L的最小值。

样例输入

5
1 3 4 2 5

样例输出

34

样例说明

这个样例就是问题描述中的例子。如果你得到了35，说明你算得有问题，请自行检查自己的算法而不要怀疑是样例输出写错了。
评测用例规模与约定
　　对于30%的评测用例，1 ≤ n ≤ 10，1 ≤ ti ≤ 20；
　　对于60%的评测用例，1 ≤ n ≤ 100，1 ≤ ti ≤ 100；
　　对于100%的评测用例，1 ≤ n ≤ 1000，1 ≤ ti ≤ 10000。

---

思路解析

这道题很容易想到哈夫曼编码的做法，但是需要注意的是，我们不能够改变初始的字母的顺序，那么就不能够使用哈夫曼编码的方法进行解决问题。那么进行作图我们仔细观察会发现：

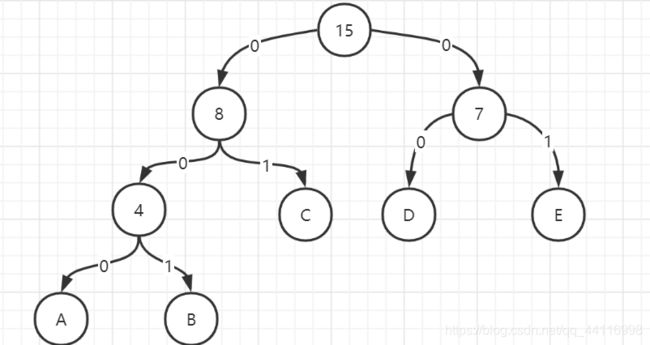
按照题目所给的编码方式:A:000, B:001, C:01, D:10, E:11,
那么其实编码的位数与所在的层数是一致的，那么结合不改变字母的顺序，我们直到，只有相邻的两两合并这种方式才能解决问题。可能会想：层数合并与这道题的关系紧密吗？
我们可以这样想：每个字母的频率作为权重，每个字母的编码位数作为层数：
原则上二叉树的权值计算为：3×1+3×3+2×4+2×2+2×5=34；
其实就相当于：

		3x1:  3被加了一次；
		3x3:  3被加了两次；
		2x4:  2被加了四次；
		以此类推，相当于合并次数。

所以,这道题就可以转化为如何找出两两合并的最小值的问题，这个问题是典型的基础动态规划问题。
可自己找网络资源查看即可（很普遍）。

---

代码解析

//4
#include
#include
#include
using namespace std;

int dp[1001][1001];   //表格关 系
vector<int> num;      //每一个字母的频率值
vector<int> sum;      //累计和

int main()
{
     
	ios::sync_with_stdio(false);
	cin.tie(0);
	int n, value;
	cin >> n;
	for (int i = 0; i < n; ++i) {
     
		cin >> value;
		num.push_back(value);
		if (i == 0)
			sum.push_back(value);
		else
			sum.push_back(sum[i - 1] + value);
		dp[i][i] = 0;  
	}
	for (int v = 2; v <= n; ++v) {
         //最少两个一起合并
		for (int i = 0; i + v - 1 < n; ++i) {
     
			int j = i + v - 1;
			int s = sum[j] - sum[i] + num[i];   //i-j之间一共的频率和
			dp[i][j] = 0x0fffffff;
			for (int k = i; k < j; ++k) {
     
				dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s);   //寻找最优值
			}
		}
	}
	cout << dp[0][n - 1];
	return 0;
}

测试结果