黑吉辽沪冀晋六省联考 2017 BZOJ 4868&4869&4870&4871&4872&4873
趁着网络上题解还不是很多,赶快怒写一发骗一下访问量
这套题在BZOJ上的题号是4868~4873。
感觉还不错,就是有一些题弄起来有一点小恶心……
这套题的部分分给得都很多,很良心的QAQ
BZOJ 4868 [Shoi2017]期末考试
枚举+贪心
枚举i表示第i天出完,把i之后的贪心挪到i即可。
#includeBZOJ 4869 [Shoi2017]相逢是问候
广义欧拉定理
我们假装c永远和模数p互质(不是题目里的c,p,是在一般情况下要做c ^ b % p的c和p),那根据欧拉定理,指数b就可以变成b%phi(p)。由于p是奇数则phi(p)必是偶数,p是偶数则phi(p)必至少减半,因此如果有形如:c ^ c ^ c ^…^ c ^ a,其实只要至多考虑前2log个指数即可,超过这些之后指数就恒为0,实际上就可以直接算出来,也就是一个定值,说明到后面就算不断修改这个点等于没改。然后我们直接暴力修改直到这个数不变,均摊是O(nlog)的。
如果c不和p互质,有一个东西叫广义欧拉定理(因为这东西降幂是O(log)级别的,因此也叫求幂大法),甩链接:http://blog.csdn.net/guhaiteng/article/details/52588223
注意用广义欧拉定理的时候必须当且仅当指数大于phi(p),否则不能直接加一个phi(p)上去……
然后这样子做,预处理理论上是O(nlog^3)的,实际上当迭代到很小的时候phi(p)会比较小,那我们记搜即可。还有就是虽然看上去要降幂2log次,实际上远不可达,实测迭代6层就可以通过本题……
不知道有没有别的复杂度更优秀的做法?
#include
using namespace std;
namespace runzhe2000
{
typedef double db;
typedef long long ll;
int n, m, p, c, a[N], phi[H], pos[N], nocnt, vis[M][H], g[M][H], h[M][H], ex[H];
struct node{int val, next;}no[N*H];
int gcd(int a, int b){return b?gcd(b,a%b):a;}
int fpow(int a, int b, int p, int &moded) // a ^ b mod phi[p]
{
bool flag = (a==c && bif (flag && vis[b][p]) return moded = h[b][p], g[b][p];
int r = 1, bb = b, tmpmoded = moded = 0;
for(; b; b>>=1)
{
if(b&1)
{
if((ll)r*a >= phi[p] || tmpmoded) moded = 1, r = (ll)r*a%phi[p];
else r *= a;
}
if((ll)a*a >= phi[p]) tmpmoded = 1, a = (ll)a*a%phi[p];
else a *= a;
}
return flag ? (vis[bb][p] = 1, h[bb][p] = moded, g[bb][p] = r) : r;
}
int get_phi(int x)
{
int r = x;
for(int i = 2, ii = sqrt((db)x); i <= ii; i++) if(x % i == 0)
{
r = (ll) r * (i-1) / i;
for(; x % i == 0; x /= i);
}
if(x != 1) r = (ll) r * (x-1) / x;
return r;
}
int get_pow(int a, int cnt, int p, int &moded)
{
if(!cnt) return fpow(a, 1, p, moded);
int pre = get_pow(a, cnt - 1, p + 1, moded);
ex[p] && moded ? pre += phi[p+1] : 0;
return fpow(c, pre, p, moded);
}
struct seg{int need, sum;}t[N*5];
void pushup(int x)
{
t[x].sum = (t[x<<1].sum + t[x<<1|1].sum) % p;
t[x].need = t[x<<1].need || t[x<<1|1].need;
}
void build(int x, int l, int r)
{
if(l == r){t[x].sum = no[pos[l]].val, t[x].need = no[pos[l]].next; return;} int mid = (l+r)>>1;
build(x<<1,l,mid); build(x<<1|1,mid+1,r); pushup(x);
}
int query(int x, int l, int r, int ql, int qr)
{
if(ql <= l && r <= qr) return t[x].sum; int mid = (l+r)>>1, ret = 0;
if(ql <= mid) (ret += query(x<<1, l, mid, ql, qr)) %= p;
if(mid < qr) (ret += query(x<<1|1, mid+1, r, ql, qr)) %= p;
return ret;
}
void modi(int x, int l, int r, int ql, int qr)
{
if(!t[x].need) return; int mid = (l+r)>>1;
if(l == r)
{
if(no[pos[l]].next)
{
pos[l] = no[pos[l]].next;
t[x].sum = no[pos[l]].val;
t[x].need = no[pos[l]].next;
}
return;
}
if(ql <= l && r <= qr)
{
if(t[x<<1].need) modi(x<<1,l,mid,ql,qr);
if(t[x<<1|1].need) modi(x<<1|1,mid+1,r,ql,qr);
}
else
{
int mid = (l+r)>>1;
if(ql <= mid) modi(x<<1,l,mid,ql,qr);
if(mid < qr) modi(x<<1|1,mid+1,r,ql,qr);
}
pushup(x);
}
void main()
{
scanf("%d%d%d%d",&n,&m,&p,&c);
phi[0] = p; ex[0] = gcd(p, c) != 1;
for(int i = 1; i < H; i++)
{
phi[i] = get_phi(phi[i-1]);
ex[i] = gcd(phi[i], c) != 1;
}
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
no[pos[i] = ++nocnt] = (node){a[i], 0};
for(int j = 1, tmp; j < H; j++)
{
no[++nocnt] = (node){get_pow(a[i], j, 0, tmp), 0};
no[nocnt-1].next = nocnt;
}
}
build(1,1,n);
for(; m--; )
{
int type, l, r; scanf("%d%d%d",&type,&l,&r);
if(!type) modi(1,1,n,l,r);
else printf("%d\n",query(1,1,n,l,r));
}
}
}
int main()
{
runzhe2000::main();
}BZOJ 4870 [Shoi2017]组合数问题
矩阵快速幂
考虑组合数的实际意义,那这个式子就是在求nk个数里取数满足取出的数个数模k为r的方案数。矩阵快速幂优化递推即可。
#includeBZOJ 4871 [Shoi2017]摧毁“树状图”
树形DP。
从来没写过这么长的DP方程……不过好在没有调特别久?
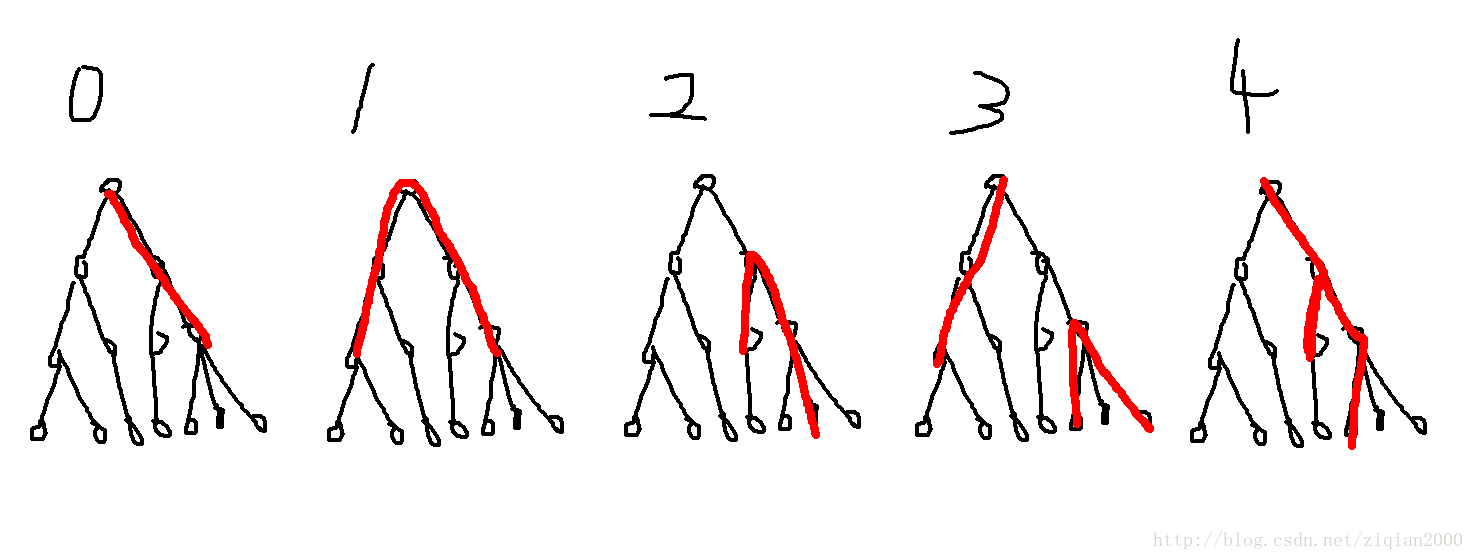
题意就是要在一棵树上找两条边不相交的链,使得去掉链后联通块数量最大。考虑可能的两条链的所有位置情况,总结一下,发现我们只需要维护一些形态的DP值(语文能力不好,怕口胡失败,特意画了一张图。图丑勿喷QAQ)。
分别记 f[i][0,1,2,3,4] 表示i的子树内,五种不同形态的链交,能在i子树能划分出的最多联通块个数。五种形态的链交分别是:
状态0:以根为一个端点的一条链
状态1:经过根的一条链(根可以也为其端点,即可以包含状态0)
状态2:不经过根的一条链
状态3:以根为一个端点的一条链+不经过根的一条链,且保证二者不相交
状态4:以根为一个端点的链或者2叉链或者3叉链(图示是2叉链,当然可以包含状态0)
有了这些DP值之后,考虑需要找的两条链的具体位置情况:
如果两条链不相交,分别设两个链上的最高点为链顶。两个链定的LCA要么是其中一个链顶,要么是一个其他点。如果是一个其他点则可以从状态1或2转移。否则分两种情况,要么两个链顶直接相连,要么中间隔了一段链。类似地可以用前缀后缀最值搞一搞。
如果相交,那链交一定是一个爪子一样的东西。那就只要用状态4和状态0搞一搞也就行了。
#includeBZOJ 4872 [Shoi2017]分手是祝愿
高斯消元或推式子
先说高斯消元的做法:
记一个点按或者不按为1或0,这样就相当于一个异或方程组。要求这个方程每个变量总和最小的解,显然这是唯一的。而且要解它并不用高斯消元,只要从高位到低位一个一个确定即可。
考虑一个局面,假设这时候最小需要h步。接下来随机一个按一个开关。如果按到需要按的h个开关之一,则还要按h-1步,否则就还要按h+1步(证明:假设按h个开关之外的其它开关之后仍有h步的解,也就是说原来的局面还存在一个h+1的解。考虑异或方程,显然不可能即存在步数为h又存在步数为h+1的解,请自行脑补)。
也就是记f[i]表示当前局面要按i次,期望结束步数,从f[i-1],f[i+1]转移即可,这样是一个三元方程。可以列出一堆方程。考虑每个式子都只有三个变量,可以 O(n) 大力消元。
这样写完可以有95分,你要问我剩下的5分在哪?有一组数据也许是强行构造,使得消元的时候分母在模意义为0,也就是没有逆元,就炸了(出题人orz)
然后把整个方程组倒过来消就可以水过这个题。不过还是能卡就是了……
(推式子的做法详见这个代码下面)
#include我们把高斯消元里的每一次消元都手动展开,加上边界情况,联立起来瞎几把推一下就有:
f[n−i]=f[n−i−1]∗(n−i−1)!∗i!∑ik=0Ckn(n−i)!
然后我调了半天没调出来,近乎崩溃。
后来弱弱地回想起来答案要乘一个阶乘…好气啊
#includeBZOJ 4873 [Shoi2017]寿司餐厅
最大权闭合子图
这题有给m=0的部分分,考虑每一次选择的区间都不会相交。因此暴力DP一个即可。
然后我就掉进了DP的坑里好久……考虑怎么DP都没办法记录哪些编号已选,那就不能DP。这题的限制都是贡献只有一次,考虑流。一个大区间选了就必选小区间,这就是最大权闭合子图的模型……然后上最小割即可。
#include