重读微积分(一):极限
文章目录
- 1 状态变化
- 2 极限语言
- 3 序列与函数
1 状态变化
如果将数学整体划分为三类,那么这三大领域可以是代数、几何以及分析。对于前两者,我们很早就建立了直观的理性概念,对于空间结构及其性质的研究,即为几何;以数为核心的研究领域,即为代数。
然而分析这个词本身具备相当多的非数学的内涵,所以初学者往往难以看透数学分析所指向的数学本质,如果简单地望文生义,那么会更倾向于将“分析”单纯地理解为一门数学技巧,而非数学领域。
我们最先接触数学分析时,是将其等同为微积分的。可以认为微积分是数学分析最基本的知识对象,而微积分的理论基础建立在极限之上。所以,我们可以将极限作为分析学的根基,为此,需要去理解极限的本质,而极限本身来说,是一个动态的过程,例如下面这个重要极限
lim x → 0 s i n ( x ) x = 1 \lim_{x\to 0}\frac{sin(x)}{x}=1 x→0limxsin(x)=1对于上式,表示当x趋于0的时候,这个分式的值为1,需要注意的一点是,这里是等于号,而非约等。当我们以初等的观念去理解这个等式的时候,会自动附加一些特殊的约定:
- x → 0 x\to0 x→0即 x = 0 x=0 x=0
- 0是有阶数的,对于 0 m 0 n \frac{0^m}{0^n} 0n0m,当 m > n m>n m>n时,值为0, m < n m<n m<n时,值为无穷大, m = n m=n m=n时,值为常数。
- s i n 0 sin0 sin0和 0 0 0具有相同的阶数,且二者相等。
我们可以很方便地通过上面的三个约定去计算一切涉及到 s i n 0 sin0 sin0和 0 0 0的比值问题。当然,这种理解并不自然,随着我们接触到的极限表达式越来越多,我们需要更多的约定来促使极限理论趋于完整。
我们可以用一种动态的眼光去审视上面这个极限,考虑到画图的方便,我们对上式稍作改动,
lim x → ∞ x s i n ( 1 x ) = 1 \lim_{x\to\infty}xsin(\frac{1}{x})=1 x→∞limxsin(x1)=1
画图方法有很多,在此使用R语言,在RStudio中画出,之所以用RStudio,是因为其界面对初学者来说更友好。输入
> x = c(1:100) #定义x为1到100的数组
> y = x*sin(1/x)
> plot(x,y,type='l',xlab='x',ylab='y=x·sin(1/x)') #画图
得到
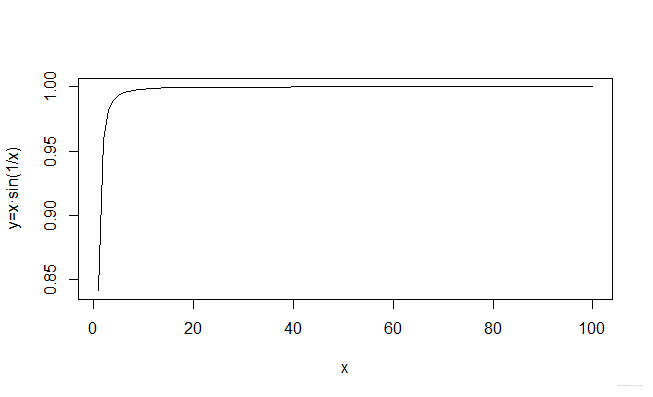
可以非常清晰地看到,当x逐渐变大的时候,y是趋于1的。这种直观的趋势可以让我们更加容易地理解极限,即作为一种动态过程。这样的理解也有助于形成对分析学的更加直观的印象——分析是建立在状态变化上的一种动态的数学。
我们一旦建立了这种动态的思维,就会发现原本安定本分的数学世界也发生了微妙的变化,例如,我们又将如何理解1这个整数。
例如无限循环小数0.999...=1这个反直觉的等式是否严格。从初等的观点来看,我们可以很容易得到 10 ⋅ 0.999... = 9.999... → ( 10 − 1 ) ∗ 0.999... = 9 → 0.999... = 1 10 \cdot 0.999...=9.999...\to (10-1)*0.999...=9\to0.999...=1 10⋅0.999...=9.999...→(10−1)∗0.999...=9→0.999...=1。
也可以很敏锐地发现,如果我们用一种不厌其烦的方式去求解分式 1 1 \frac{1}{1} 11,会非常自然地得到0.999...
但无论如何,0.999...=1这种表达是反直觉的,反来自于初等数学的直觉。换句话说,初等数学可能无法解决这种极限问题,我们需要一个更加严格的有关极限的定义和表示,尤其需要建立一种可以称之为相等的映射关系。
2 极限语言
初学数学分析的时候,很多人包括我在内,都对 ε − N \varepsilon-N ε−N这种表达方式深恶痛绝,更妙的是,不理解这种表达方式,对做题似乎影响不大。我们大部分人通过加深对上面的那三个约定(以及更多约定)的记忆来完成解题,而非通过加深对数学对象的理解来实现这一目的。
其实这个语句并不难理解,当我们最开始接触无穷大这个概念的时候,是在描述自然数的个数。那时我们常说的可能是,无论你举出一个多么大的自然数,我都能举出一个更大的数,所以自然数是无穷的。
那么,现在我们有一个数列 { x n } \{x_n\} { xn},如果这个当n趋近于无穷大的时候,如果 x n x_n xn也趋于无穷大,我们理应用相同的方式来表述,即无论你举出一个多么大的数 E E E,我都可以找到一个n,使得 x n > E x_n>E xn>E。当然,和自然数不同,这个数列未必单调,也未必发散,所以我们需要另加上一句对于所有m>n有 x m > E x_m>E xm>E。这样就能确保我们的这个数列 x n > E x_n>E xn>E是发散的了。
至此,我们已经对无穷极限做出了一个规范的定义:
假定对于任意大的 E > 0 E>0 E>0,都存在正整数 N N N,使得一切的 n > N n>N n>N,不等式
∣ x n ∣ > E |x_n|>E ∣xn∣>E成立,则称序列 x n {x_n} xn的极限是 ∞ \infty ∞,记作 lim n → ∞ x n = ∞ \lim_{n\to\infty}x_n=\infty limn→∞xn=∞。
对于有穷极限亦然,同样对于数列 { x n } \{x_n\} { xn},如果当 n → ∞ n\to\infty n→∞时, x n = a x_n=a xn=a,那么我们可以说,无论你拿出一个多么大的 n n n,那么对于所有更大的 n n n,都使得 x n x_n xn更接近 a a a。 ε \varepsilon ε就是对这种更接近的一种描述,由此而得到了对有穷极限的定义:
假定对于任意小的 ε \varepsilon ε,都存在正整数 N N N,使得对于一切的 n > N n>N n>N,不等式
∣ x n − a ∣ < ε |x_n-a|<\varepsilon ∣xn−a∣<ε则称序列 { x n } \{x_n\} { xn}以 a a a为极限,或者收敛于 a a a,记为 lim n → ∞ x n = a \lim_{n\to\infty}x_n=a limn→∞xn=a。
在这样的极限观点下,我们再回头看待上文中所列举的两个式子,可能会显得更加严谨。首先,对于重要极限 lim x → ∞ x s i n ( 1 x ) = 1 \lim_{x\to\infty}xsin(\frac{1}{x})=1 limx→∞xsin(x1)=1,假设 ε = 0.01 \varepsilon=0.01 ε=0.01,那么选取 N = 10 N=10 N=10,
> x = c(10,100)
> y = 1-x*sin(1/x)
> > plot(x,y,type='l',xlab='x',ylab='y=1-x·sin(1/x)')
我们可以得到一个新的图像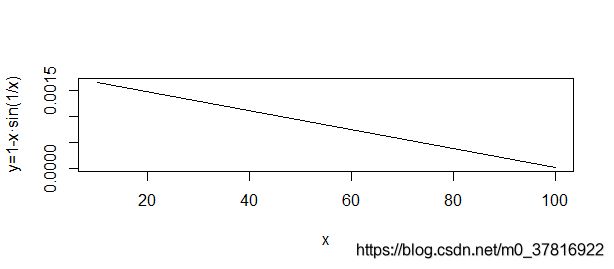
可见,当 x > N x>N x>N时, ∣ x s i n ( 1 x ) − 1 ∣ < ε |xsin(\frac{1}{x})-1|<\varepsilon ∣xsin(x1)−1∣<ε。由于 ε \varepsilon ε的选取是任意的,所以我们可以继续减小 ε \varepsilon ε的值,但无论 ε \varepsilon ε小到什么程度,我们都可以找到一个 N N N,使之满足极限的定义式。
对于0.999...我们可以构造一个数列 y = 1 − 0. 1 x y=1-0.1^x y=1−0.1x,当 x → ∞ x\to\infty x→∞时, y → 0 y\to0 y→0,也就是说,对于任意小的一个 ε \varepsilon ε,我们总能找到一个 N N N,使得 x > n x>n x>n时, 0. 1 x < ε 0.1^x<\varepsilon 0.1x<ε。
3 序列与函数
如果从映射这个角度去考察序列与函数,那么二者最大的区别源自定义域。序列是定义域为正整数的特殊函数。相比之下,我们所接触的大多名之为函数的映射,定义域多为实数。这就导致在函数的定义域中,我们随便抽选出一个元素个数大于1的区间,其元素个数都是无穷多的。即对于区间 [ a , b ] [a,b] [a,b]而言,只要 a ̸ = b a\not =b a̸=b,那么这个区间中的元素个数就是无穷多个。
这种差别导致了我们在理解函数的困难,但并不意味着二者不能相互借鉴。极限在 ε − N \varepsilon-N ε−N意义上对相等的定义,让我们意识到,初等数学视角上的一一对应的相等可能是有缺陷的。有了极限的概念之后,我们知道每一个实数实则包含了无穷多种初等的表示,即 1 = 0.999...0 = 0.999...1 = 0.999... n , n 1=0.999...0=0.999...1=0.999...n,n 1=0.999...0=0.999...1=0.999...n,n为任意长度的数串,中间的无穷多位,导致末位信息在极限相等的角度上变得毫无意义。
这时我们会异想天开地希望建立整数与实数的对应关系,例如将整数环映射到区间 [ − 1 , 1 ] [-1,1] [−1,1]内,这个区间也会出现刚刚所说的某种实数区间的性质,即任意一个长度大于一的子区间,都有无穷多个元素。当然,这是不切实际的,因为众所周知,实数的个数是比整数更高的无穷,也就是说实数区间 [ − 1 , 1 ] [-1,1] [−1,1]的元素个数是远多于整数的。
但是在极限的定义下,这可能是一种有效的类比。如果在实数区间 [ − 1 , 1 ] [-1,1] [−1,1]里,当 x → 0 x\to\ 0 x→ 0时, y ( x ) = y 0 y(x)=y_0 y(x)=y0,我们便可以说,对任意小的 ε > 0 \varepsilon>0 ε>0,都存在一个整数 δ \delta δ,使得区间 [ − δ , δ ] [-\delta,\delta] [−δ,δ]内的 x x x都满足 ∣ y 0 − y ( x ) ∣ < ε |y_0-y(x)|<\varepsilon ∣y0−y(x)∣<ε。一旦这个式子成立,我们就可以说对于任意小的一个 δ \delta δ,我们都可以在整数映射的那个区间 [ − 1 , 1 ] [-1,1] [−1,1]中找到无穷多个 δ ′ < δ \delta'<\delta δ′<δ,从而在区间 [ − δ ′ , δ ′ ] [-\delta',\delta'] [−δ′,δ′]内存在同样的极限。
当然,通过整数除以正无穷得到 [ − 1 , 1 ] [-1,1] [−1,1]的一个子区间,似乎在技术上是不可实现的,因为我们没法用 ∞ \infty ∞做分母,对于表达式 n ∞ \frac{n}{\infty} ∞n来说,当 n ̸ = ∞ n\not= \infty n̸=∞时,其值为0,否则为不定式,超出了我们的理解能力。
这时,我们可以用一种更动态的眼光去看待整数映射的 [ − 1 , 1 ] [-1,1] [−1,1]。对于任意小的一个 δ \delta δ,我们都可以在整数环中找到一个 N N N,使得在序列 − 1 , − ( N − 1 ) N , . . . − 1 N , 0 , 1 N . . . 1 -1,\frac{-(N-1)}{N},...\frac{-1}{N},0,\frac{1}{N}...1 −1,N−(N−1),...N−1,0,N1...1中找到 δ ′ < δ \delta'<\delta δ′<δ,其中 δ ′ = N δ ′ N \delta'=\frac{N_{\delta'}}{N} δ′=NNδ′,使得区间整数映射区间的子区间 [ − δ ′ , δ ′ ] [-\delta',\delta'] [−δ′,δ′]内,满足 ∣ y 0 − y ( x ) ∣ < ε |y_0-y(x)|<\varepsilon ∣y0−y(x)∣<ε。
如果跳出数学抽象,那么这里的 δ \delta δ和 δ ′ \delta' δ′都是具备现实意义的。对于没怎么接触过编程的人来说,第一眼看到我们上面所画出的图,必然会想当然地认为,这张图是连续的。他不会清楚地意识到,这只不过是不到100个点的一种拟合。即便我们真的用无穷多个点画出了这条曲线,但屏幕在显示的时候仍旧是以像素的形式,这个曲线仍旧是有分立的点连接而成的,只不过这些个分立的点足够稠密,以至于可以骗过我们的眼睛。
所以,可以认为 δ \delta δ是人眼的一种分辨极限,当两个点的距离小于 δ \delta δ时,便无法区分这两个点是否分离。那么,当我们画图的时候,只要确保两个点的距离 δ ′ < δ \delta'<\delta δ′<δ,就会自然地在我们的眼中形成连续的图像。也就是说,如果我们的区间长度为 L L L,那么只要选取 L δ ′ \frac{L}{\delta'} δ′L个点来画图,我们的视觉就会欺骗我们。
当然,我们此后会接触更多的让人摸不着头脑的函数,这些函数过于奇葩,以至于上面的这些似乎完全不适用呢。。。