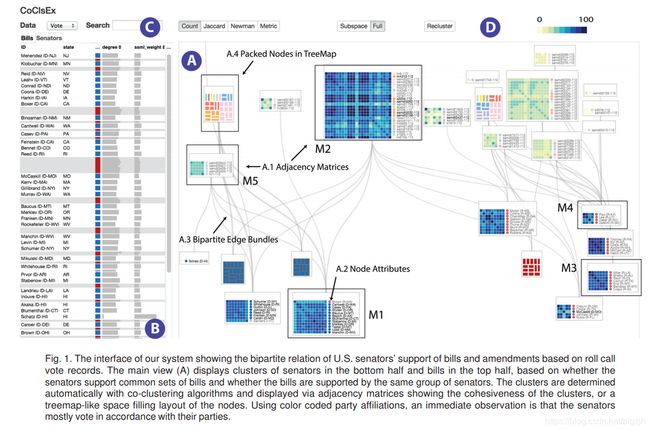
Interactive Visual Co-Cluster Analysis of Bipartite Graphs
论文传送门
作者
博世北美研究所
- Panpan Xu
上海纽约大学
- Nan Cao
香港科技大学
- Huamin Qu
佐治亚理工学院:
- John Stasko
Abstract
二分图模拟了两种不同类型实体之间的关系。例如,它适用于描述人们与不同社会群体的联系或他们与感兴趣的主题的联系。在这些应用中,理解二分图中实体之间的连接模式是很重要的。例如,对于人和他们感兴趣的主题之间的二分关系,人们可以基于他们的共同兴趣形成组,并且主题也可以基于感兴趣的观众来分组或分类。共聚类方法可以识别这种连接模式,并同时在两种类型的实体中找到聚类。在本文中,我们提出了一种交互式可视化设计,它结合了共聚类方法,以便于识别由二分图中的公共连接形成的节点簇。除了突出显示自动检测到的节点簇和它们之间的连接之外,可视化界面还提供了用于评估簇中两部分连接的同质性、识别潜在异常值以及分析节点属性与簇结构的相关性的可视化提示。交互式可视界面允许用户通过直接操作(即,分割和合并聚类)或通过提供关于聚类质量的明确反馈来灵活地调整节点分组,以结合他们的领域的先验知识,基于该反馈,系统将学习共同聚类算法的参数化,以更好地与用户的节点相似性的概念一致。为了展示该系统的实用性,我们在真实数据集上展示了两个示例使用场景。
Introduction
贡献:
- 任务分析和设计一个可视化分析系统,通过灵活的节点分组对二分图中的连接模式进行探索性分析。
- 一种新算法,应用拉普拉斯正则化度量学习(LRML) ,一种有效的度量学习方法,用于二分图的半监督共聚类分析。
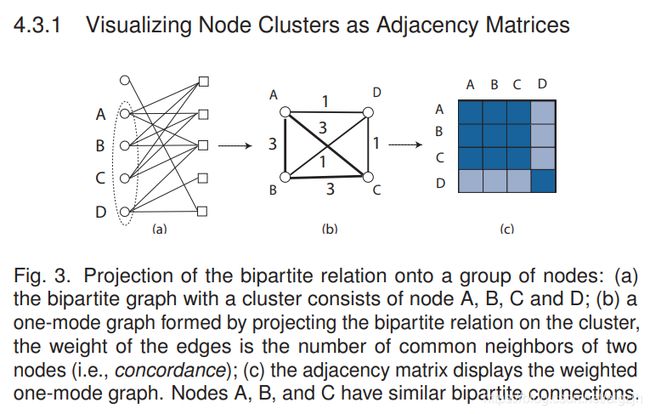
- 一种灵活的可视化设计,用于在二分图中表示集群,分别通过邻接矩阵和树形图说明集群中节点的关系模式和特征模式。
Background
- 二分图
- Co-clustering 联合聚类
Related Work
- Graph Visualization
- Bipartite and Multimodal Graph Visualization
- Co-clustering Visualization
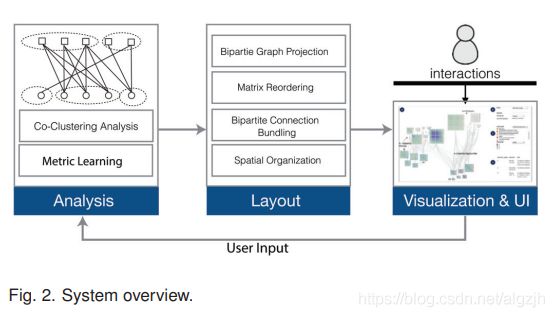
System Design and Implementation
Requirements:
- 确定两组之间的节点连接
- 确定每种类型节点的具体属性值
- 识别两种类型中相似的节点。
- 分析连通性模式与特定领域节点属性的相关性
- 通过二分关系解释节点簇
- 探索子空间集群
- 评估和优化节点集群
Bipartite Graph
G = ( U , V , E ) G=(U, V, E) G=(U,V,E)
biadjacency matrix
B ∥ U ∥ × ∥ V ∥ B_{\|U\| \times\|V\|} B∥U∥×∥V∥
Laplacian Regularized Metric Learning (LRML)
d ( u i 0 , u i 1 ) A = ( B i 0 ⋅ − B i 1 ) T A ( B i 0 ⋅ − B i 1 ) d\left(u_{i_{0}}, u_{i_{1}}\right)_{A}=\sqrt{\left(B_{i_{0}} \cdot-B_{i_{1}}\right)^{T} A\left(B_{i_{0}} \cdot-B_{i_{1}}\right)} d(ui0,ui1)A=(Bi0⋅−Bi1)TA(Bi0⋅−Bi1)
A Laplacian regularization term is also included in the optimization goal
min A ⪰ 0 ∑ ( u i , u i 1 ) ∈ S d ( u i 0 , u i 1 ) A \min _{A \succeq 0} \sum_{\left(u_{i}, u_{i_{1}}\right) \in S} d\left(u_{i_{0}}, u_{i_{1}}\right)_{A} minA⪰0∑(ui,ui1)∈Sd(ui0,ui1)A
+ λ ∑ u i 0 ∈ U ∑ u i 1 ∈ U w ( u i 0 , u i 1 ) d ( u i 0 , u i 1 ) A +\lambda \sum_{u_{i_{0}} \in U} \sum_{u_{i_{1}} \in U} w\left(u_{i_{0}}, u_{i_{1}}\right) d\left(u_{i_{0}}, u_{i_{1}}\right)_{A} +λ∑ui0∈U∑ui1∈Uw(ui0,ui1)d(ui0,ui1)A
− ε log ( det ( A ) ) -\varepsilon \log (\operatorname{det}(A)) −εlog(det(A))
w ( u i 0 , u i 1 ) = { 1 , if u i 0 ∈ N ( u i 1 ) 0 , otherwise w\left(u_{i_{0}}, u_{i_{1}}\right)=\left\{\begin{array}{l}1, \text { if } u_{i_{0}} \in N\left(u_{i_{1}}\right) \\ 0, \text { otherwise }\end{array}\right. w(ui0,ui1)={ 1, if ui0∈N(ui1)0, otherwise
Visual Representation
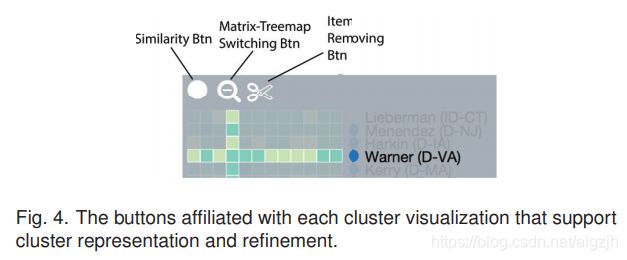
前面描述的任务和要求指导了我们的可视化设计。我们采用了两种集群的图标视觉表示,分别受 NodeTrix 和 Dicon 启发的 adjacency 矩阵和树形图。这些表示是可切换的,用于揭示集群内节点的关系(R3,R5,R6,R7)和属性(R2,R4)模式。主视图是水平分割的,一组节点和集群位于顶部,另一组位于底部。它们由聚合的二分链路(R5)连接。我们还提供了一组相互作用来探索和完善共团簇(R6,R7)。
User Interaction
- Details-on-demand (R1)
- Subspace selection (R6)
- Cluster refinement (R7)
Sample Usage Scenarios
- US Senate Votes
- Interpretation of co-clustering results
- Semi-supervised co-cluster analysis
- Publication Data
Expert Review
为了评估系统的可用性和潜在效用,我们采访了专家用户(表示为E1和E2),他们是机器学习领域的高级研究人员,专门研究主动学习技术,以及非专家用户(表示为E3和E4),他们是具有社会和政治科学领域知识的研究生
Conclusion
我们介绍了一个交互式可视化分析系统,用于分析二分图中的聚类。我们使用邻接矩阵和树形图对聚类进行可视化编码。我们通过两个真实数据集的案例研究来说明所提出的技术。我们的调查发现了许多有趣的发现,有助于说明该系统的有用性。未来,我们计划将该系统应用于分析其他应用领域的二分图,进行用户研究,并扩展该系统的功能,不仅用于分析二分图,还用于分析多模图。