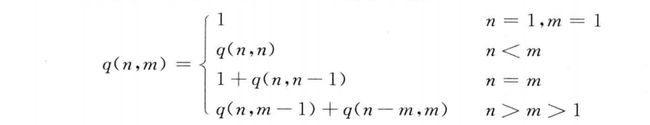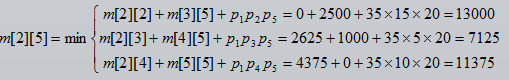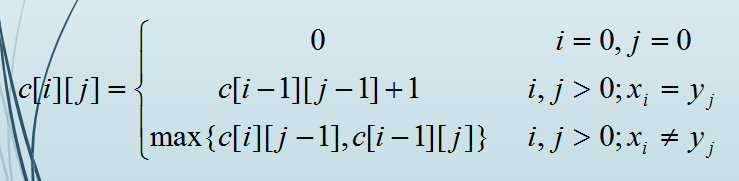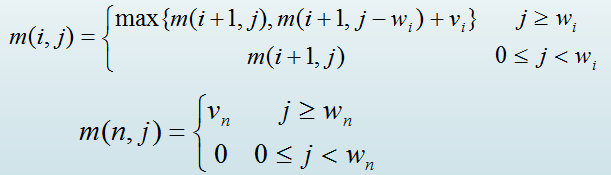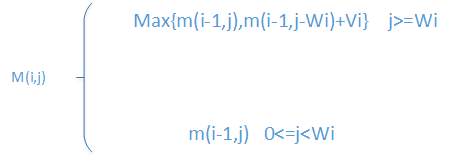算法期末复习笔记

                                                     第一章算法引论

1.算法时间复杂度

 

                                          第二章 递归与分治策略

一.算法设计思想

分治法的设计思想是，将一个难以直接解决的大问题，分隔成一些规模较小的相同问题，以便各个击破。

二.整数划分问题

根据n和m的关系，考虑以下几种情况： 
1. 当n=1时，不论m的值为多少（m>0)，只有一种划分即{1}; 
2. 当m=1时，不论n的值为多少，只有一种划分即n个1，{1,1,1,...,1}; 
3. 当n=m时，根据划分中是否包含n，可以分为两种情况： 
    (1) 划分中包含n的情况，只有一个即{n}； 
    (2) 划分中不包含n的情况，这时划分中最大的数字也一定比n小，即n的所有(n-1)划分。因此 f(n,n) =1 + f(n,n-1); 
4. 当n5. 但n>m时，根据划分中是否包含最大值m，可以分为两种情况： 
    (1) 划分中包含m的情况，即{m, {x1,x2,...xi}}, 其中{x1,x2,... xi} 的和为n-m，可能再次出现m，因此是（n-m）的m划分，因此这种划分个数为f(n-m, m); 
    (2) 划分中不包含m的情况，则划分中所有值都比m小，即n的(m-1)划分，个数为f(n,m-1);因此 f(n, m) = f(n-m, m)+f(n,m-1);

public static int q(int n,int m){
  if((n<1)||(m<1))
     return 0;
  if(n==1||m==1)
     return 1;
  if(n

三.合并排序

1.递归算法实现

public static void mergeSort(Comparable a[], int left, int right)
   {
      if (left

2.递推算法实现

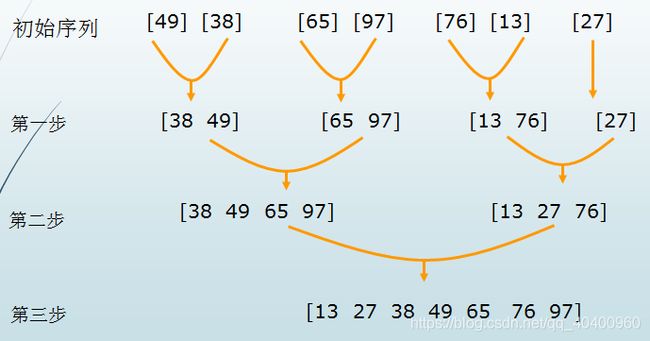
算法思想：首先将数组a中相邻元素两两配对，使用合并算法将他们排序，构造n/2组长度为2的排好序的子数组段，然后再将他们排序成长度为4的排好序的子数组段，如此进行下去，直至整个数组排好序。

 最坏时间复杂度：O(nlogn)

平均时间复杂度：O(nlogn)

辅助空间：O(n)

稳定性：稳定

四.快速排序算法

1.快速排序算法思想

①设置两个变量I、J，排序开始的时候：I=0，J=N-1； 　　

②以第一个数组元素作为关键数据，赋值给key，即 key=A[0]； 　　

③从J开始向前搜索，即由后开始向前搜索（J=J-1），找到第一个小于key的值A[J]，并与A[I]交换；

④从I开始向后搜索，即由前开始向后搜索（I=I+1），找到第一个大于key的A[I]，与A[J]交换； 　　

⑤重复第3、4、5步，直到 I=J； (3,4步是在程序中没找到时候j=j-1，i=i+1，直至找到为止。找到并交换的时候i， j指针位置不变。另外当i=j这过程一定正好是i+或j-完成的最后另循环结束。)

⑥采用同样的方法，对左边的组和右边的组进行排序，直到所有记录都排到相应的位置为止。

注：注意开始的关键X永远不变，永远是和X进行比较，无论在什么位子，最后的目的就是把X放在中间，小的放前面大的放后面。

2.算法思想举例：

一趟排序之后

［27 38 13］ 49 ［76 97 65 49］

二趟排序之后

［13］ 27 ［38］ 49 ［49 65］76 ［97］

三趟排序之后

13 27 38 49 49 ［65］76 97

最后的排序结果

13 27 38 49 49 65 76 97

 3.代码实现

package 排序算法;

/**
 * Created by mafx on 2018/12/11.
 * @author mafx.
 * 快速排序
 */
public class QuickSort {


    public static void main(String[] args) {
        int[] array={27,99,0,8,13,64,86,16,7,10,88,25,90};
        sort(array,0,array.length-1);
        for (int i:array) {
            System.out.print(i+" ");
        }

    }
    public static void sort(int[] array,int low,int hight){
        if(low=pivotkey){
                hight--;
            }
            swap(array,low,hight);
            while (low=array[low]){
                low++;
            }
            swap(array,low,hight);
        }
        return low;
    }

    public static void swap(int[]array,int i,int j){
        int temp=array[i];
        array[i]=array[j];
        array[j]=temp;
    }
}

4.快速排序算法总结

①快速排序算法的性能取决于划分的对称性。通过修改算法partition，可以设计出采用随机选择策略的快速排序算法。

②在快速排序算法的每一步中，当数组还没有被划分时，可以在a[p:r]中随机选出一个元素作为划分基准，这样可以使划分基准的选择是随机的，从而可以期望划分是较对称的。

③最坏时间复杂度：O(n2)    平均时间复杂度：O(nlogn)    辅助空间：O(n)或O(logn)    稳定性：不稳定

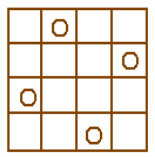
五.循环赛日程表问题

1.算法要求

设计一个满足以下要求的比赛日程表：

(1)每个选手必须与其他n-1个选手各赛一次；

(2)每个选手一天只能赛一次；

(3)循环赛一共进行n-1天。

2.算法思想

按分治策略，将所有的选手分为两半，n个选手的比赛日程表就可以通过为n/2个选手设计的比赛日程表来决定。递归地用对选手进行分割，直到只剩下2个选手时，比赛日程表的制定就变得很简单。这时只要让这2个选手进行比赛就可以了。

3.算法思想实例

依据1、2可将比赛日程表设计成有n行和n-1列的表。在表中第i行和第j列处填入第i个选手在第j天所遇到的选手。

左上角与左下角的2小块分别为选手1至选手4以及选手5至选手8前三天的比赛日程，据此，将左上角小块中的所有数字按照其相对 位置抄到右下角，将左下角小块中的所有数字按照其相对 位置抄到右上角。

                                                   第三章动态规划

一.算法设计总体思想

①动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题

②但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解时，有些子问题被重复计算了许多次。

③如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。

二.动态规划基本设计步骤

①找出最优解的性质，并刻画其结构特征。

②递归地定义最优值。

③以自底向上的方式计算出最优值。

④根据计算最优值时得到的信息，构造最优解。

三.动态规划算法的基本要素：

1.最优子结构

   （1） 矩阵连乘计算次序问题的最优解包含着其子问题的最优解。这种性质称为最优子结构性质。

   （2）在分析问题的最优子结构性质时，所用的方法具有普遍性：首先假设由问题的最优解导出的子问题的解不是最优的，然后 再设法说明在这个假设下可构造出比原问题最优解更好的解，从而导致矛盾。

   （3）利用问题的最优子结构性质，以自底向上的方式递归地从子问题的最优解逐步构造出整个问题的最优解。最优子结构是问题能用动态规划算法求解的前提

2.重叠子问题

  （1）递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称为子问题的重叠性质。

 （2）动态规划算法，对每一个子问题只解一次，而后将其解保存在一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。

 （3）通常不同的子问题个数随问题的大小呈多项式增长。因此用动态规划算法只需要多项式时间，从而获得较高的解题效率。

3.备忘录方法

   （1）备忘录方法的控制结构与直接递归方法的控制结构相同，区别在于备忘录方法为每个解过的子问题建立了备忘录以备需要时查看，避免了相同子问题的重复求解。

四.矩阵连乘问题

1.分析最优解得结构

特征：计算A[i:j]的最优次序所包含的计算矩阵子链 A[i:k]和A[k+1:j]的次序也是最优的。

2.递归的定义最优解

设计算A[i:j]，1≤i≤j≤n，所需要的最少数乘次数m[i,j]，则原问题的最优值为m[1,n] ，当i=j时，A[i:j]=Ai，因此，m[i,i]=0，i=1,2,…,n，当i，这里Ai的维数为

/**
*p[]数组用于存储所有矩阵的行数+最后一个矩阵的列数
*
*m[i][j]表示Ai矩阵乘到Aj矩阵的最优解
*
*s[i][j]一个整数k,表示两个矩阵间的断开位置
*
*
*/
public static void matrixChain(int [] p, int [][] m, int [][] s)
   {
      int n=p.length-1;
      for (int i = 1; i <= n; i++) m[i][i] = 0;
      for (int r = 2; r <= n; r++)//跨度
         for (int i = 1; i <= n - r+1; i++) {
            int j=i+r-1;//末尾矩阵的下标
            m[i][j] = m[i+1][j]+ p[i-1]*p[i]*p[j];//默认从i开始的第一个处分隔
            s[i][j] = i;
            for (int k = i+1; k < j; k++) {//选择不同的分隔点，获取最优的位置
               int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];//小跨度的全部已经算过，可以直接使用
               if (t < m[i][j]) {
                 m[i][j] = t;
                 s[i][j] = k;}
               }
            }
   }

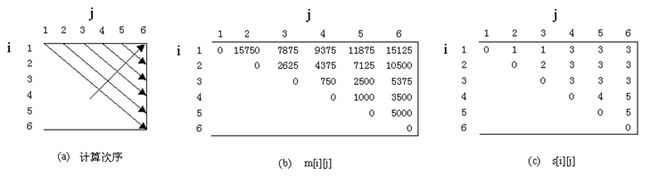
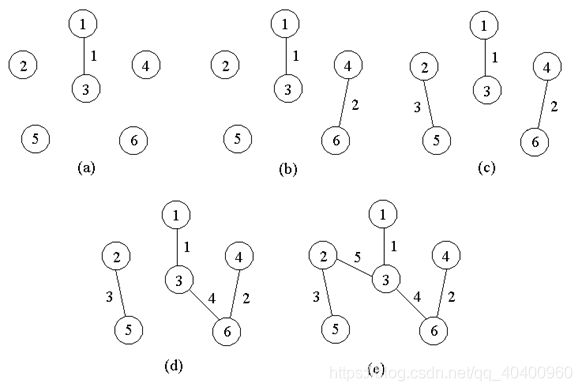
计算方法：

数组p:

i初始从1开始表示第一个矩阵，按照图（a）的箭头的计算顺序开始计算以第i个矩阵开始第j个矩阵结束的计算次数最小值，计算公式为​：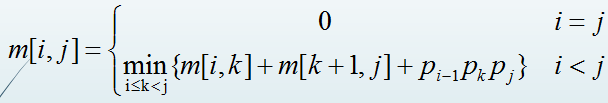

其中K则表示大于i小于j的断开位置，将m[i][j]最小值记录在图（b）对应位置，将m[i][j]取最小值时的k值存储在图（c）的对应位置用来记录在哪里断开。

最终所得到的划分结果为：(A1(A2A3))((A4A5)A6)

 五.最长公共子序列

#include
#include
#include
#include
#include
using namespace std;
 int dp[205][205];
int main(){
  char a[205],b[205];
  while(~scanf("%s%s",(a+1),(b+1))){
       int lena=strlen(a+1);
       int lenb=strlen(b+1);
      for(int i=1;i<=lena;i++){//ÕâÒ»¶¨ÊÇ=ºÅ
         for(int j=1;j<=lenb;j++){
                if(a[i]==b[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                   dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }

         }
      }
      cout<

 注：每个公共序列肯定是以某个公有字符结尾的字串

六.0-1背包问题

1.从前往后装

m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。 

当J>=Wi时可能放入，有可能不放入，取决于是否能够达到价值最大

当j

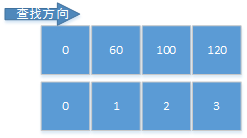
举例：

重量：{0，1,2,3}

价值：{0，60,100,120}

背包容量为：5

i=3时是提前初始化的部分

2.从后往前装

注：m(i,j)表示将前i件物品放入容量为j的背包中的最大价值

 

七.流水作业调度问题

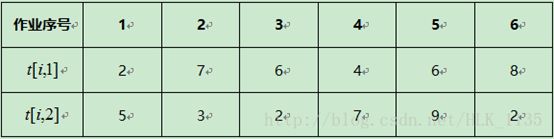
流水作业调度问题的Johnson算法

①令

②将N1中作业依ai的递增排序；将N2中作业依bi的递减排序；

③N1中作业接N2中作业构成满足Johnson法则的最优调度。

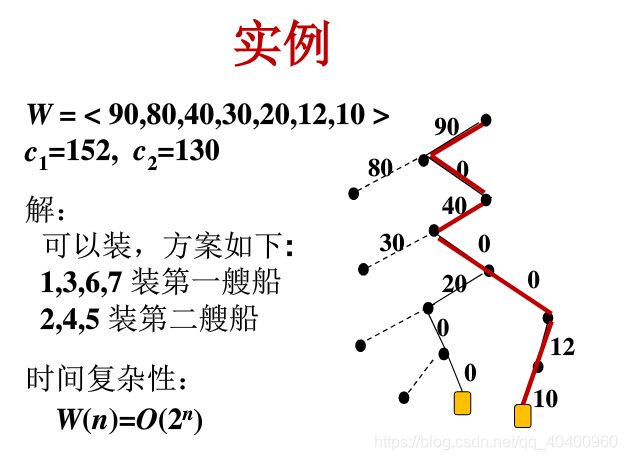
算法在计算执行时间的过程如下图所示：

作业执行次序为：1，4，5，2，6，3

最有时间35

 

                                            第四章贪心算法

一.贪心算法的基本要素

1.贪心选择性质：所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素，也是贪心算法与动态规划算法的主要区别。

2.最优子结构性质：当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。

二.贪心算法与动态规划算法的差异
 

1.动态规划算法通常以自底向上的方式解各个子问题，而贪心算法则通常以自顶向下的方式进行。

2.动态规划算法每部所做的选择往往依赖于子问题的解，因而只有在解出相关子问题时才能做出选择。而贪心算法，仅仅在当前状态下做出最优选择，即局部最优选择。贪心算法需要满足贪心选择性质。

三.活动安排问题

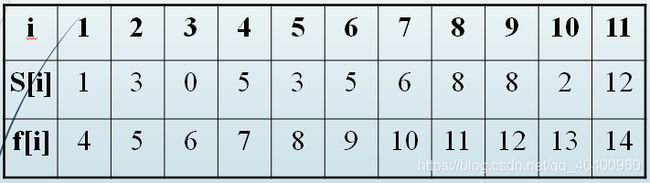
1.算法思路：将输入的活动以其结束时间的非递减序排列，每次总是选择具有最早完成时间的相容活动加入集合A中。

排列后的活动：

2.代码：

public static int greedySelector(int [] s, int [] f, boolean a[])
{
      int n=s.length-1;
      a[1]=true;
      int j=1;
      int count=1;
      for (int i=2;i<=n;i++)
      {
        if (s[i]>=f[j]) {//选择相容的活动
           a[i]=true;//如果活动相容则将其标记为可选
           j=i;
           count++;
        }
        else a[i]=false;
      }
      return count;
}

 最终的选择结果是：1,4,8,11

四.背包问题

算法步骤（贪心选择策略）：

①首先计算每种物品单位重量的价值Vi/Wi，按单位重量的价值从大到小排序，然后，依贪心选择策略，将尽可能多的单位重量价值最高的物品装入背包。

②若将这种物品全部装入背包后，背包内的物品总重量未超过C，则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直地进行下去，直到背包装满为止。

五.最优装载问题

算法描述：最优装载问题可用贪心算法求解。采用重量最轻者先装的贪心选择策略，可产生最优装载问题的最优解。

六.哈夫曼编码问题

1.算法步骤：

①初始化，统计各字符出现的概率，根据概率的大小给字符排序。          

②把两个概率最小的字符的概率加起来，形成一个新的概率。

③把这个新的概率看成是一个新字符的概率，并与其他字符概率重新排序。

④重复步骤（1）~（3）到最后概率等于1为止。

2.算法举例：

①概率统计

②绘制哈夫曼树（规定：合并概率时将概率小的复制为0）

③编码结果

平均码长为：2×0.3+4×0.08+4×0.11+1×0.37+3×0.14=2.15（位） 

3.总结

①前缀码：对每一个字符规定一个0,1串作为其代码，并要求任一字符的代码都不是其它字符代码的前缀。这种编码称为前缀码

②关于n个字符的哈夫曼算法的计算时间为O(nlogn)

③表示最优前缀码的二叉树总是一棵完全二叉树，即树中任一结点都有2个儿子结点。

七.单源最短路径

1.算法思想

其基本思想是，设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。

初始时，S中仅含有源。设u是G的某一个顶点，把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径，并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u，将u添加到S中，同时对数组dist作必要的修改。一旦S包含了所有V中顶点，dist就记录了从源到所有其它顶点之间的最短路径长度。

2.算法举例

3.总结

算法时间复杂度：

八.最小生成树问题

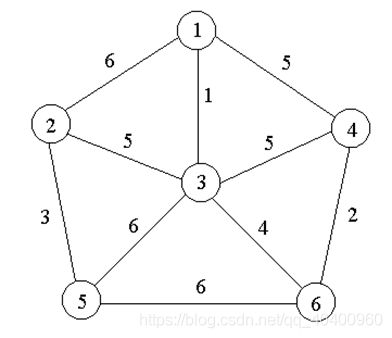
求下图的最小生成树：

1.Prim算法

①算法思想

设G=(V,E)是连通带权图，V={1,2,…,n}。

首先置S={1}，只要S是V的真子集，就作如下的贪心选择：

选取满足条件iS，jV-S，且c[i][j]最小的边，将顶点j添加到S中。这个过程一直进行到S=V时为止。

②算法举例

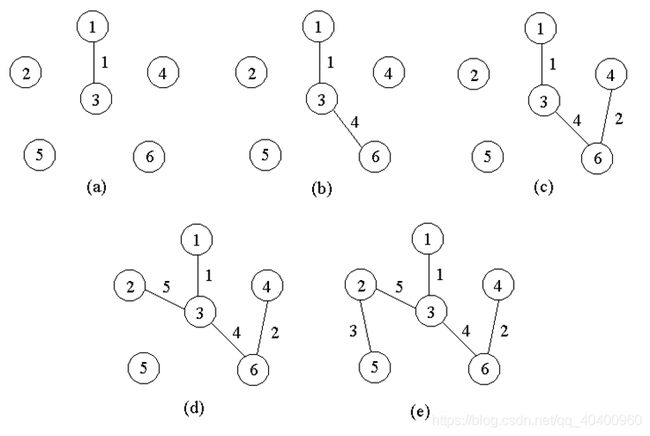
2.Kruskal算法

①算法思想

Kruskal算法构造G的最小生成树的基本思想是，首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小到大排序。

从第一条边开始，依边权递增的顺序查看每一条边，并按下述方法连接2个不同的连通分支：当查看到第k条边(v,w)时，如果端点v和w分别是当前2个不同的连通分支T1和T2中的顶点时，就用边(v,w)将T1和T2连接成一个连通分支，然后继续查看第k+1条边；如果端点v和w在当前的同一个连通分支中，就直接再查看第k+1条边。这个过程一直进行到只剩下一个连通分支时为止。

②算法举例

                                                   第五章回溯法

一.回溯法的基础知识

1.回溯法解题的3个步骤：

     （1）针对所给问题，定义问题的解空间；

     （2）确定易于搜索的解空间结构；

     （3）以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

2.常用剪枝函数：

用约束函数在扩展结点处剪去不满足约束的子树；

用限界函数剪去得不到最优解的子树。

3.回溯的实现方式

递归回溯：

  回溯法对解空间作深度优先搜索，因此，在一般情况下用递归方法实现回溯法。

void backtrack (int t){
       if (t>n) 
          output(x);
       else
         for (int i=f(n,t);i<=g(n,t);i++) {
            x[t]=h(i);
            if (constraint(t)&&bound(t)) 
               backtrack(t+1);
         }
}

迭代回溯：

采用树的非递归深度优先遍历算法，可将回溯法表示为一个非递归迭代过程。

void iterativeBacktrack ()
{
  int t=1;
  while (t>0) {
    if (f(n,t)<=g(n,t)) 
      for (int i=f(n,t);i<=g(n,t);i++) {//f(n,t)和g(n,t)分别表示在当前扩展节点处未搜索过的子树的起始编号和终止编号。
        x[t]=h(i);
        if (constraint(t)&&bound(t)) {//剪枝
          if (solution(t)) output(x);//判断是否找到解，若找到则输出
          else t++;}
        }
    else t--;
    }
}

4.子集树和排列树

①子集树（部分）：当所给的问题是从n个元素的集合S中找出S满足某种性质的子集时，相应的解空间树被称作子集树。遍历子集树需O(2^n)计算时间

举例：0-1背包问题、装载问题、符号三角形问题、n后问题、最大团问题

②排列树（全部的排列）：当所给问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。遍历排列树需要O(n!)计算时间

举例：批处理作业调度问题、旅行售货员问题

二.装载问题（子集树）

装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上这2艘轮船。如果有，找出一种装载方案。

1.算法思想

容易证明，如果一个给定装载问题有解，则采用下面的策略可得到最优装载方案。

首先将第一艘轮船尽可能装满；

将剩余的集装箱装上第二艘轮船。

将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集，使该子集中集装箱重量之和最接近。

2.算法举例

①先对货物重量进行由大到小进行排序

②对第一艘轮船进行最优装载

三.批处理作业调度（排列树）

批处理作业调度问题要求对于给定的n个作业，制定最佳作业调度方案，使其完成时间和达到最小。

注：完成时间和并不是整个任务的完成时间，而是每个任务完成所需时间的总和

1.算法举例

 

Tji	机器1	机器2
作业1	2	1
作业2	3	1
作业3	2	3

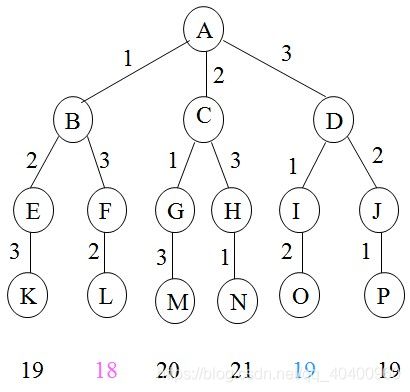
 这3个作业的6种可能的调度方案是1,2,3；1,3,2；2,1,3；2,3,1；3,1,2；3,2,1；它们所相应的完成时间和分别是19，18，20，21，19，19。易见，最佳调度方案是1,3,2，其完成时间和为18。

解空间：

2.完成时间和计算方法

说明：f1表示机器1完成处理时间，x[]数组用于记录每个作业在机器1上的工作时间

f2[]数组用于记录每个作业在机器2上完成处理时间，f是以某种调度顺序进行调度的完成时间和

f1+=m[x[j]][1];//每个作业在机器1的完成处理时间等于它前边的所有作业在该机器的工作时间（有等待时间）

f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+m[x[j]][2];//如果前一个作业在机器二上的完成时间很大，如果存在f2[i-1]>f1的情况，则当前的作业在机器二上还需要等待，所以此时f2[i]=f2[i-1]+m[x[j]][2];否则f2[i]=f1+m[x[j]][2]

f+=f2[i];//总完成时间和为，机器而完成时间之和

四.n皇后问题

1.算法举例

4后问题的搜索空间：

每个节点有4个儿子，分别代表选择1,2,3,4列位置。

得出的解：

五.0-1背包问题

六.旅行售货员问题（货郎问题）

1.算法举例

2. 搜索空间

                                                        第六章分支界限法

一.分支界限法与回溯法的不同

1.求解目标

回溯法的求解目标是找出解空间树中满足约束条件的所有解。

分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。

2.搜索方式的不同

回溯法以深度优先的方式搜索解空间树。

分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。

二.分支界限法基本思想

1.在分支限界法中，每一个活结点只有一次机会成为扩展结点。

2.活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。

3.此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。

三.常见的两种分支界限法

1.队列式(FIFO)分支限界法

         按照队列先进先出（FIFO）原则选取下一个节点为扩展节点。

2.优先队列式分支限界法

         按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

四.单源最短路径问题（优先队列式分支界限法、极小堆）

1.算法思想

解单源最短路径问题的优先队列式分支限界法用一极小堆来存储活结点表。其优先级是结点所对应的当前路长。

算法从图G的源顶点s和空优先队列开始。结点s被扩展后，它的儿子结点被依次插入堆中。此后，算法从堆中取出具有最小当前路长的结点作为当前扩展结点，并依次检查与当前扩展结点相邻的所有顶点。

如果从当前扩展结点i到顶点j有边可达，且从源出发，途经顶点i再到顶点j的所相应的路径的长度小于当前最优路径长度，则将该顶点作为活结点插入到活结点优先队列中。这个结点的扩展过程一直继续到活结点优先队列为空时为止。

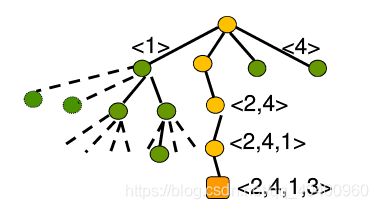
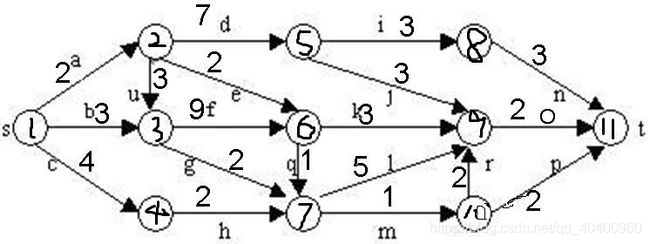
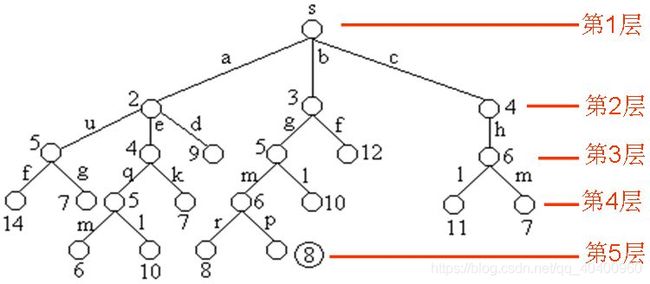
2.算法举例

算法先从源节点s开始扩展，3个子结点2,3,4被插入到队列当中，如下图所示。

取出结点2，它有3个子树。结点2沿边f扩展到3时，路径长度为5，而结点3的当前路径为3(s->6)，没有得到优化，该子树被剪掉。.结点2沿边d，e扩展值5,6时，将他们加入优先队列，如图

取出头结点3，它有两个子树。结点3沿f边扩展到结点6时，该路径长度为12，而结点6的当前路径为4，该路径没有被优化，该子树被剪枝。结点3沿g扩展到7时，将7加入到优先队列。如下如所示

重复上面操作直到队列为空。s到各个结点的最短路径。

注：①某节点被取出则说明到该节点的路径已经达到最优

②每次只有使用队头最小的那个路径长加上自己的子节点路径才可能达到对其他节点的优化

五.0-1背包问题（优先队列、最大堆）

1.算法思想

首先，要对输入数据进行预处理，将各物品依其单位重量价值从大到小进行排列。

在下面描述的优先队列分支限界法中，节点的优先级由已装袋的物品价值加上剩下的最大单位重量价值的物品装满剩余容量的价值和。

算法首先检查当前扩展结点的左儿子结点的可行性。如果该左儿子结点是可行结点，则将它加入到子集树和活结点优先队列中。当前扩展结点的右儿子结点一定是可行结点，仅当右儿子结点满足上界约束时才将它加入子集树和活结点优先队列。当扩展到叶节点时为问题的最优值。

六.最大团问题（优先队列、最大堆）

七.批处理作业调度问题（优先队列、最小堆）

八.旅行售货员问题（优先队列、最小堆）

                                               第七章概率算法

一.基本概念

1.概率算法的一个特征是，对所求解问题的同一实例用同一概率算法求解两次可能得到完全不同的效果。

2.概率算法有四类：数值概率算法、蒙特卡罗算法、拉斯维加斯算法、舍伍德算法

二.蒙特卡罗算法

1.用于求问题的准确解。

2.用蒙特卡罗算法能求得问题的一个解，但这个解未必是正确的。

3.求得正确解的概率依赖于算法所用的时间。算法所用的时间越多，得到正确解的概率就越高。

三.拉斯维加斯算法

1.一旦用拉斯维加斯算法找到一个解，这个解就一定是正确解。但有时用拉斯维加斯算法找不到解。（拉斯维加斯算法不会得不到不正确的解）

2.找到正确解的概率随着它所用的计算时间的增加而提高。

3.对于所求问题的任一实例，用同一拉斯维加斯算法反复对该实例求解足够多次，可使求解失败的概率任意小。

四.舍伍德算法

1.舍伍德算法总能求得问题的一个解，且所求得的解总是正确的。

2.当一个确定性算法在最坏情况下的计算复杂性与其在平均情况下的计算复杂性有较大差别时，可在这个确定性算法中引入随机性将它改造成一个舍伍德算法。

五.数值概率算法

1.概率算法常用于数值问题的求解。

2.这类算法所得到的往往是近似解，且近似解的精度随计算时间的增加而不断提高。

3.在许多情况下，要计算出问题的精度解是不可能的或没有必要的，因此，用数值概率算法可以的得到相当满意的解。

                                        第八章NP完全性理论

一.基本概念

1.P类问题：所有可以在多项式时间内求解的判定问题构成P类问题。

2.NP类问题：所有的非确定性多项式时间可解的判定问题构成NP类问题。

3.NP-完全问题：NP中的某些问题的复杂性与整个类的复杂性相关联。这些问题中任何一个如果存在多项式时间的算法，那么所有NP问题都是多项式时间可解的。这些问题被称为NP-完全问题(NPC问题)。