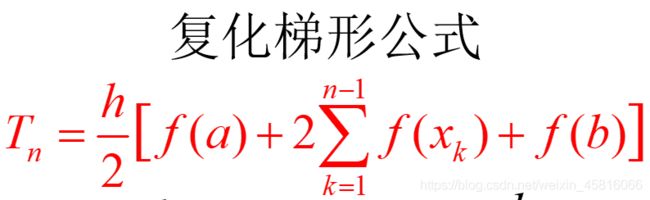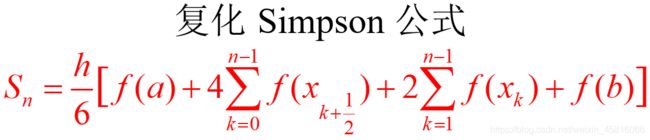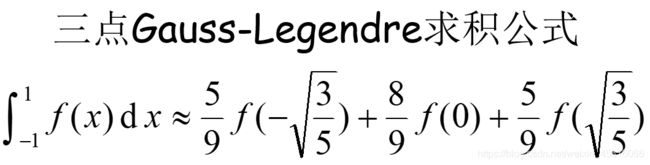数值积分 python代码实现
老规矩,数学原理什么的就不写了。
直接贴代码和实例演示,以下代码基于python和numpy。
在这里,我将用代码实现复化梯形算法、复化 Simpson 算法、Romberg 积分算法和三点 Gauss-Legendre求积算法。
这四种方法求的都是,函数在一段定义域内的积分值。
往期博客:
线性方程组的迭代法 python代码实现
函数插值法之牛顿插值法 python代码实现
数值微分 python代码实现
python计算信息熵、信息增益和信息增益率
数值积分
- 复化梯形算法
-
- 定义函数
- 参数说明
- 实例运行
- 复化 Simpson 算法
-
- 定义函数
- 参数说明
- 实例运行
- Romberg 积分算法
-
- 定义函数
- 参数说明
- 实例运行
- 三点 Gauss-Legendre求积算法
-
- 定义函数
- 参数说明
- 实例运行
- 总结
复化梯形算法
复化梯形公式如下图所示:
首先
import numpy as np
定义函数
以下便是我定义的函数:
def tx_fh(x0,f,n=2**5):
a=x0[0]
b=x0[1]
if type(f) is np.ndarray:
y=2*np.sum(f)-f[0]-f[-1]
tn=((b-a)/(f.shape[0]-1))*y/2
else:
x=np.linspace(a,b,n+1)
y=2*np.sum(f(x))-f(a)-f(b)
tn=((b-a)/n)*y/2
print(tn)
return tn
参数说明
“x0”指的是自变量的定义域。
“f”可以是函数关系或者是确定值,后续可以看到两者区别。
“n”指的是将定义域分为n等份。
实例运行
拿个实例运行一下,在这个实例中,“f”是一个函数关系。
x=np.array([0,1])
f=lambda x:4/(1+x**2)
tx_fh(x,f,2**3)
得出以下结果:
3.1389884944910893
再试验一下代入的“f”是确定值的情况,这种适用于不知道函数关系的情况。
不过,为了对比以及方便,我在演示时,用函数关系生成了一个确定值数组“f”。
x=np.array([0,1])
x0=np.linspace(x[0],x[1],9)
f=lambda x:4/(1+x**2)
y0=f(x0)
print('y0=',y0)
tx_fh(x,y0)
得出以下结果:
y0= [4. 3.93846154 3.76470588 3.50684932 3.2 2.87640449 2.56 2.26548673 2. ]
3.1389884944910893
复化 Simpson 算法
复化 Simpson 公式如下图所示:
定义函数
以下便是我定义的函数:
def simpson_fh(x0,f,n=2**5):
a=x0[0]
b=x0[1]
if type(f) is np.ndarray:
f1=f[1::2].copy()
f2=f[0::2].copy()
y=4*np.sum(f1)+2*np.sum(f2)-f[0]-f[-1]
sn=2*((b-a)/(f.shape[0]-1))*y/6
else:
x=np.linspace(a,b,2*n+1)
x1=x[1::2].copy()
x2=x[0::2].copy()
y=4*np.sum(f(x1))+2*np.sum(f(x2))-f(a)-f(b)
sn=((b-a)/n)*y/6
print(sn)
return sn
参数说明
“x0”指的是自变量的定义域。
“f”可以是函数关系或者是确定值,后续可以看到两者区别。
不过,如果要输入确定值数组的话,数组内的元素必须是2n+1个,即奇数个,才能符合公式要求。
我在编写的时候因为主要是给自己用,所以也没写断言什么的来判断输入的是否正确,默认给的是对的。
“n”指的是将定义域分为2n等份。
实例运行
拿个实例运行一下,在这个实例中,“f”是一个函数关系。
x=np.array([0,1])
f=lambda x:4/(1+x**2)
simpson_fh(x,f,2**2)
得出以下结果:
3.141592502458707
再试验一下代入的“f”是确定值的情况,这种适用于不知道函数关系的情况。
x=np.array([0,1])
x0=np.linspace(x[0],x[1],9)
f=lambda x:4/(1+x**2)
y0=f(x0)
print('y0=',y0)
simpson_fh(x,y0)
得出以下结果:
y0= [4. 3.93846154 3.76470588 3.50684932 3.2 2.87640449 2.56 2.26548673 2. ]
3.141592502458707
综上可知,在相同的等份数下(输入的x、y0都是一样的,仅仅算法不一样),相比于复化梯形,复化 Simpson更为精确(因为上面那个函数的精确积分为pi)。
Romberg 积分算法
Romberg 积分算法的计算过程如下图所示:
定义函数
以下便是我定义的函数:
def romberg(x0,f,n):
k=0
xlb=np.zeros((4,n+3))
for i in range(n+3):
xlb[0,i]=tx_fh(x0,f,2**i)
for i in range(n+2):
xlb[1,i+1]=4*xlb[0,i+1]/3-xlb[0,i]/3
for i in range(n+1):
xlb[2,i+2]=16*xlb[1,i+2]/15-xlb[1,i+1]/15
while k<n:
xlb[3,k+3]=64*xlb[2,k+3]/63-xlb[2,k+2]/63
k+=1
k=np.arange(n+3)
xl=np.vstack([k,xlb])
print(xl.T)
print(xlb[3][3:])
return xlb[3][3:]
参数说明
“x0”指的是自变量的定义域。
“f”可以是函数关系或者是确定值。
“n”指的是得到n个Romberg 积分值,也就是得到R1~Rn。
实例运行
x=np.array([0.0000001,1])
f=lambda x:np.sin(x)/x
romberg(x,f,1)
得出以下结果(下列数组对照上一张图,可知每一个值所对应的数学意义):
[[0. 0.9207354 0. 0. 0. ]
[1. 0.93979319 0.94614578 0. 0. ]
[2. 0.94451342 0.94608683 0.9460829 0. ]
[3. 0.94569076 0.94608321 0.94608297 0.94608297]]
array([0.94608297])
上面这个“array([0.94608297])”就是我们要的结果。
三点 Gauss-Legendre求积算法
三点 Gauss-Legendre求积公式如下图所示:
定义函数
以下便是我定义的函数:
def gauss_l3(x0,f):
a=x0[0]
b=x0[1]
t1=-(b-a)*0.6**0.5/2+(b+a)/2
t2=(b+a)/2
t3=(b-a)*0.6**0.5/2+(b+a)/2
y=((5*f(t1)+8*f(t2)+5*f(t3))/9)*(b-a)/2
print(y)
return y
参数说明
“x0”指的是自变量的定义域。
“f”指的是函数(以后再实现不是函数,而是确定值的)。
实例运行
x=np.array([0.0000001,1])
f=lambda x:np.sin(x)/x
gauss_l3(x,f)
得出以下结果:
0.9460830340784266
可以看出,相比于Romberg 积分算法,三点 Gauss-Legendre求积算法不用迭代,所以能够更快的得到答案。
总结
在相同的等份数下,相比于复化梯形,复化 Simpson更为精确。
相比于Romberg 积分算法,三点 Gauss-Legendre求积算法不用迭代,所以能够更快的得到答案。
但是三点 Gauss-Legendre求积算法有个缺点,就是某些函数在较大定义域中的求积,使用线性变化的三点 Gauss-Legendre求积算法并不能得到正确解,大家可以试一下ex^2 ,也就是e的x平方次方在[0,100]上的积分。
不过如果使用非线性单调变化的三点 Gauss-Legendre求积算法还是有可能求到精确解的。
四者的代码总结如下:
# 复化梯形算法
def tx_fh(x0,f,n=2**5):
a=x0[0]
b=x0[1]
if type(f) is np.ndarray:
y=2*np.sum(f)-f[0]-f[-1]
tn=((b-a)/(f.shape[0]-1))*y/2
else:
x=np.linspace(a,b,n+1)
y=2*np.sum(f(x))-f(a)-f(b)
tn=((b-a)/n)*y/2
print(tn)
return tn
# 复化 Simpson 算法
def simpson_fh(x0,f,n=2**5):
a=x0[0]
b=x0[1]
if type(f) is np.ndarray:
f1=f[1::2].copy()
f2=f[0::2].copy()
y=4*np.sum(f1)+2*np.sum(f2)-f[0]-f[-1]
sn=2*((b-a)/(f.shape[0]-1))*y/6
else:
x=np.linspace(a,b,2*n+1)
x1=x[1::2].copy()
x2=x[0::2].copy()
y=4*np.sum(f(x1))+2*np.sum(f(x2))-f(a)-f(b)
sn=((b-a)/n)*y/6
print(sn)
return sn
# Romberg 积分算法
def romberg(x0,f,n):
k=0
xlb=np.zeros((4,n+3))
for i in range(n+3):
xlb[0,i]=tx_fh(x0,f,2**i)
for i in range(n+2):
xlb[1,i+1]=4*xlb[0,i+1]/3-xlb[0,i]/3
for i in range(n+1):
xlb[2,i+2]=16*xlb[1,i+2]/15-xlb[1,i+1]/15
while k<n:
xlb[3,k+3]=64*xlb[2,k+3]/63-xlb[2,k+2]/63
k+=1
k=np.arange(n+3)
xl=np.vstack([k,xlb])
print(xl.T)
print(xlb[3][3:])
return xlb[3][3:]
# 三点 Gauss-Legendre求积算法
def gauss_l3(x0,f):
a=x0[0]
b=x0[1]
t1=-(b-a)*0.6**0.5/2+(b+a)/2
t2=(b+a)/2
t3=(b-a)*0.6**0.5/2+(b+a)/2
y=((5*f(t1)+8*f(t2)+5*f(t3))/9)*(b-a)/2
print(y)
return y
2020.4.2
数学的作业压力才是第一生产力!
本来不想加入“确定值”来加强鲁棒性,可顶不住数学作业有“确定值”这种题型。