图卷积神经网络笔记——第二章:谱域图卷积介绍(1)
目录
- 一、图卷积介绍
- 二、图谱卷积的背景知识
一、图卷积介绍



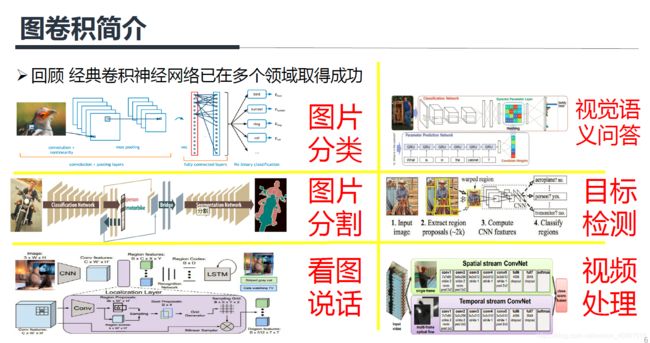

其中语音可以看作是一维向量,图像可以看作是二维矩阵,视频可以看作是三维矩阵。

其中序列无序性是指:上图中红色节点的邻居节点有两个,而我们不知道它们谁应该排在前,谁应该排在后,这就是序列无序性。维数可变性是指:上图中红色节点和蓝色节点的邻居节点个数是可以不相同的,这就是维数可变性。因此我们无法将3x3的卷积核应用到图数据上,这就是图卷积网络需要解决的问题。
![]()
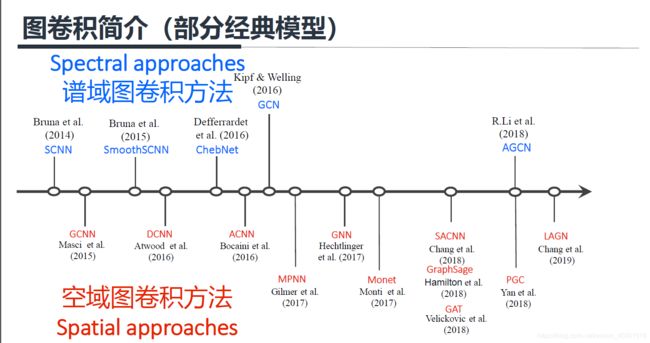
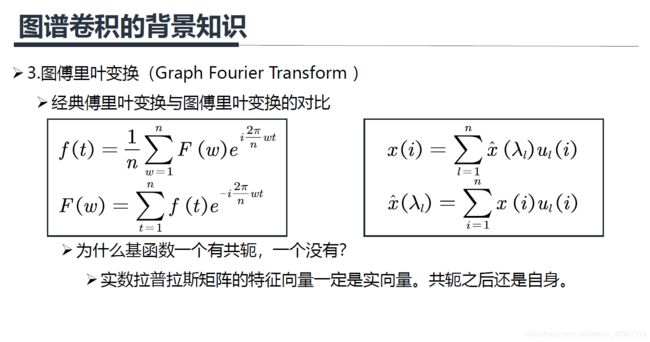
后面我会先介绍谱域图卷积方法,主要由下面圈出来的三篇文章入手,即SCNN、GCN和ChebNet三个模型。
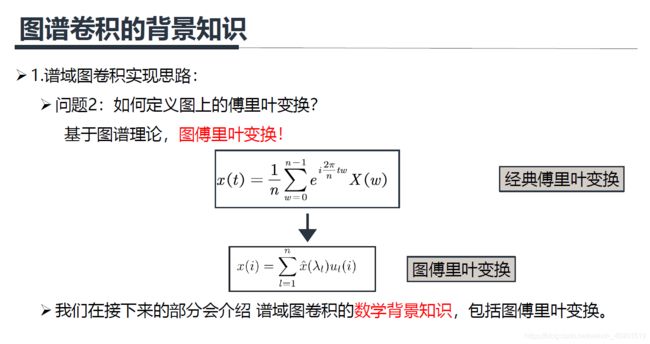
二、图谱卷积的背景知识

上面两个式子是等价的。

我们将 f 1 ( t ) f_1(t) f1(t)定义为空域输入信号, f 2 ( t ) f_2(t) f2(t)定义为空域卷积核,那么卷积核就可以这样定义:
首先将空域上的信号 f 1 ( t ) f_1(t) f1(t)转换到频域信号 F 1 ( w ) F_1(w) F1(w),然后相乘,再将相乘后的结果通过傅里叶反变换后再返回空域上去,这个就是谱域图卷积的实现思路(将空域转换到频域上处理,处理完再返回)。
回想一下前面所说的经典的卷积操作具有序列有序性和维数不变性的限制,使得经典卷积难以处理图数据,也就是说对于一个3x3的卷积核,它的形状是固定的,它的感受野的中心节点必须要有八个领域才能使用卷积核,但是图上的节点的领域节点是不确定的,此外图上节点的领域节点也是没有顺序的,这就不能直接在空域使用经典的卷积。但是当我们把数据从空域转换到频域,在频域处理数据时,只需要将每个频域的分量放大或者缩小就可以了,不需要考虑信号在空域上存在的问题,这个就是谱域图卷积的巧妙之处。

其中 V V V代表所有节点的集合(共n个), E E E代表所有边的集合, W W W代表邻接矩阵(nxn的方阵), D D D为度矩阵,定义为从 i i i节点出发的所有边的权重之和(nxn的方阵,是对角矩阵)。下面看一个例子,这个例子中的权重都为1:


上面是拉普拉斯矩阵半正定的证明,感兴趣的可以看看,其实就是展开了。



如在二维空间中有 u 1 u_1 u1, u 2 u_2 u2两个线性无关的向量,则它们可以表示这个二维空间中的所有向量,它们就是二维空间中的一组基。

上面就是在说拉普拉斯矩阵特征分解后的特征向量不但是n维空间中的一组基,而且还是正交的(相乘为0),简称标准正交基。
但是为什么拉普拉斯矩阵是度矩阵减邻接矩阵,也就是 L = D − W L=D-W L=D−W呢?原因是拉普拉斯矩阵是图上的一种拉普拉斯算子,下面接着看什么是拉普拉斯算子:



上面右图就是两个变量的离散拉普拉斯矩阵算子的形象解释,也就是说对于某个中心像素(红色)的算子为周围四个像素之和减去4倍的自己。


下面这个公式就是做了一下简单的变换,只要是理解了前面讲的几个矩阵的定义,就很好理解了,对于n个节点则由变换后的公式得出(上面右边公式)。
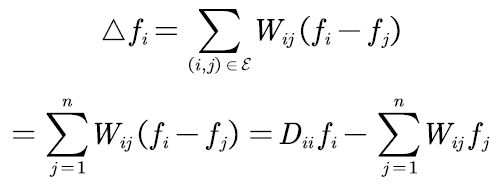


以上就是拉普拉斯矩阵的性质,正是因为有了这些性质,才会使用拉普拉斯矩阵来做以下的工作。

上图中蓝色线段代表信号的大小,类似于图像上灰度图像像素,像素越高,画的这个线段越长。图上的信号也是类似的,只不过若一个信号有 c c c个通道,那么 x = [ x 1 , x 2 , . . . , x n ] ∈ R n ∗ c x=[x_1,x_2,...,x_n] \in R^{n*c} x=[x1,x2,...,xn]∈Rn∗c,彩色图像有R,G,B三个通道,则 c = 3 c=3 c=3。下面为了讲解简单,我们先假设图上的一个信号只有一个通道,当然多个通道也是类似的。

不了解经典傅里叶变换的可以去: https://zhuanlan.zhihu.com/p/19763358.查看,下面主要看看经典傅里叶变换的物理意义是什么。

下面这个图就是上面左图。
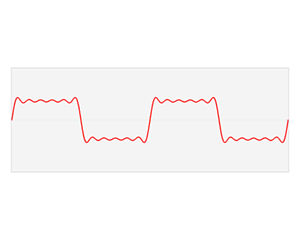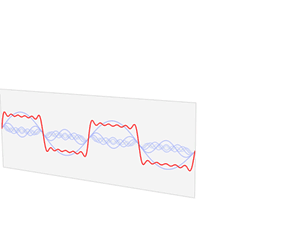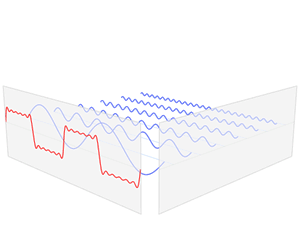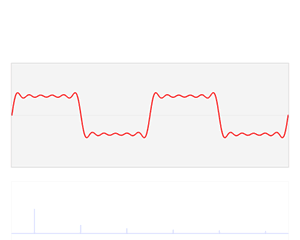
经典傅里叶变换其实就是说:一个信号由不同频率的基函数信号叠加而成,比如上图中红色信号是原信号,蓝色信号是不同频率上的基函数信号(余弦或者正弦函数)。上面右图中,红色原信号可以由不同频率的基函数线性组合而成,蓝色的高度表示基前面的系数,也就是所谓的傅里叶系数,也就是
原函数在这个基上的坐标分量。

上面的公式是离散的傅里叶变换,它和图傅里叶变换比较接近(图傅里叶变换也是离散的), F ( w ) F(w) F(w)就是上面所说的蓝线的高低。

上面左边公式是连续的傅里叶变换,右边是离散的。

上面公式的 x x x就是输入信号, x ^ ( λ 1 ) \hat x(\lambda_1) x^(λ1)就是前面提到的傅里叶系数。

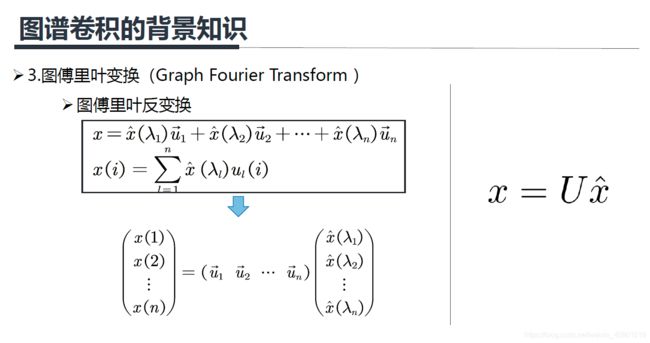
上面右边 x = U x ^ x=U\hat x x=Ux^ 中的 x ^ \hat x x^ 就是谱域上的信号。

傅里叶正变换就是求傅里叶反变换前面的系数,也就是每个基函数前面的振幅,具体做法看前面定义,也就是做输入信号 x x x 和基函数 u u u 的内积。

本征函数和本征向量可以认为是特征值和特征向量的扩展。特征向量是针对矩阵而言,而本征向量是针对算子而言的,很接近,宽泛一点可以认为是一个概念。

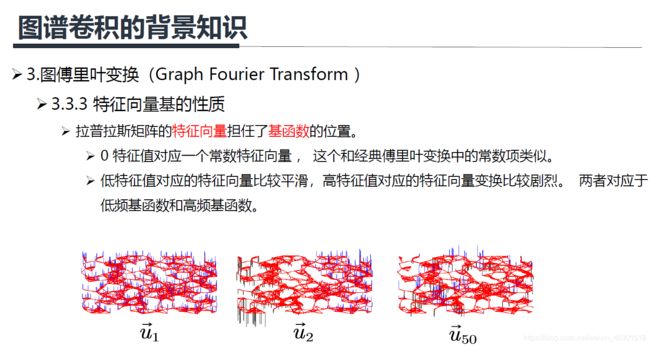
上图是三个不同的特征值对应的特征向量的示例, u 1 u_1 u1是最小的特征值对应的特征向量(可以看出很平滑), u 2 u_2 u2是第二小的特征值对应的特征向量(不太平滑), u 50 u_{50} u50是第五十小的特征值对应的特征向量(很不平滑)。

Zero crossing是指有边相邻的两个节点上对应的值一个大于0,一个小于0,每出现这样的一条边,Zero crossing就加一,通过Zero crossing的个数可以粗略的判断信号的震荡程度,或者可以说是平滑程度。从右图可以看到,大特征值可以视为高频信号,小特征值可以视为低频信号。




图上的卷积定义:先对 F ( x ) 和 F ( g ) F(x) 和F(g) F(x)和F(g)做傅里叶正变换,然后在谱域上做 h a r m a n d harmand harmand 乘积,也就是 F ( x ) ⊙ F ( g ) F(x) \odot F(g) F(x)⊙F(g),
最后通过傅里叶反变换 F − 1 F^{-1} F−1将结果返回到空域。前面讲了傅里叶正变换就是 x ^ = U T x \hat x=U^Tx x^=UTx ,则傅里叶反变换就是 U ( U T x ⊙ U T g ) U(U^Tx \odot U^Tg) U(UTx⊙UTg)。


上面这个推导感觉不是很好理解,我下面在清晰的推导一下(写公式费时间,手写一下),推导前提必须知道harmand的意思就是两个矩阵对应位置相乘(有区别与矩阵的乘法)。
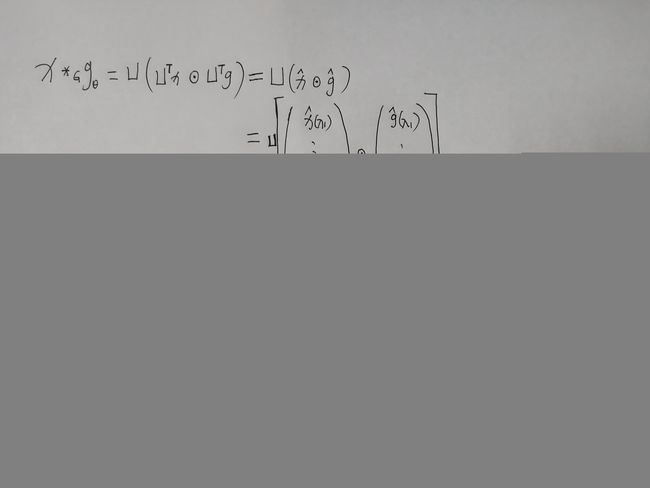
上面就是谱域图卷积最终的公式,所有的谱域图卷积的原理就是这个公式,只是对滤波器 g ^ \hat g g^ 做了不同的处理。最后多说一下这个公式的意义是:卷积核信号(或者说滤波器信号) g ^ \hat g g^ 也是一个n维的向量,它的作用是将原信号的不同的分量进行一个放大或者缩小,这取决于卷积核信号在谱域上不同元素的值。