图搜索算法（深度优先搜索、迭代加深的深度优先搜索、广度优先搜索、代价一致搜索、A*搜索）

图搜索算法

本周学习了一下图的搜索算法，包括无信息搜索算法：深度优先搜索、迭代加深的深度优先搜索、广度优先搜索以及代价一致搜索；有信息搜索算法：A*搜索。

一、需求分析

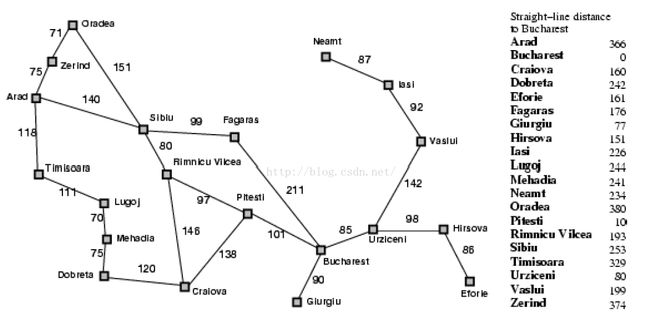
分别用深度优先搜索、迭代加深的深度优先搜索、广度优先搜索以及代价一致搜索得到从Arad到Bucharest的一条路径，即为罗马尼亚问题的一个解，然后输出每个解的单源路径，并计算、输出每个算法花费的时间开销然后进行比较。

 

图一：罗马尼亚地图

二、详细代码

//主函数

int main(){
Graph g=Graph();
clock_t start,end;
cout<<"1、深度优先搜索:"<

 

//打印路径函数

void show(Graph g,stack s){
stack s1=s,s2=s,s3=s;
int result=0;
if(s1.size()==0){
cout<<"路径搜索失败..."<"<"<

 

//图类

class Graph{
private:
//城市名
charcities[20][20]={"Arad","Zerind","Oradea","Timisoara","Sibiu","Lugoj","RimnicuVilcea","Fagaras","Mehadia","Drobeta","Craiova","Pitesti","Bucharest","Giurgiu","Urziceni","Hirsova","Eforie","Vaslui","Isi","Neamt"};
intpath[20][20]={{0,75,10000,118,140,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{75,0,71,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,71,0,10000,151,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{118,10000,10000,0,10000,111,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{140,10000,151,10000,0,10000,80,99,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,111,10000,0,10000,10000,70,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,80,10000,0,10000,10000,10000,146,97,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,99,10000,10000,0,10000,10000,10000,10000,211,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,70,10000,10000,0,75,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,75,0,120,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,146,10000,10000,120,0,138,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,97,10000,10000,10000,138,0,101,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,211,10000,10000,10000,101,0,90,85,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,90,0,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,85,10000,0,98,10000,142,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,98,0,86,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,86,0,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,142,10000,10000,0,92,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,92,0,87},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,87,0}};
int mark[20];//标志访问函数
//启发式函数
intH[20]={516,524,530,479,403,394,343,326,391,392,310,160,150,155,100,0};
public:
//构造函数
Graph(){
init();
} 
//访问标志初始化
void init(){
for(int i=0;i<20;i++)
mark[i]=0;
}
//第一个孩子 
int getFirst(int start){
if(start>=0 && start<20){
for(int i=0;i<20;i++)
if(path[start][i]>0 && path[start][i]<10000) //表示start和i所表示的点有关系
return i; 
}
return -1;//表示一个孩子也没有 
}
//下一个孩子
int getNext(int start,int w){
if(start>=0 && start<20 && w>=0 && w<20){
for(int i=w+1;i<20;i++)
if(path[start][i]>0 && path[start][i]<10000)//有关联 
return i;
}
return -1;//一个孩子也没有 
}
void setMark(int i){
mark[i]=1;
}
int getMark(int i){
return mark[i];
}
int getH(int i){
return H[i];
}
int* getH(){
return H; 
}
char* getCities(int i){
return cities[i];
}
int getPath(int i,int j){
return path[i][j];
}
};

 

/**

【深度优先】

基本原理：深度优先搜索采用堆栈寻找路径，首先从Arad结点出发，判断是否为目标结点，若否，寻找与该结点的邻接点，先搜索一条分支上的所有节 点，然后再去搜索和Arad的其它分支结点，找出并存进待扩展结点表，等待扩展，每次先判断待扩展结点表是否为空，若否，则从待扩展结点表中取出一个结点 进行扩展，并将扩展后的结点存进该表，若是，则返回失败.

*/

 

//深度优先搜索类

class DFS{
private:
int x,w;//w表示第一个关联点 
stack s,ss;
public:
void DFS_Search(Graph g,int v0,int vg){
s.push(v0);
g.setMark(v0);
while(true){
x=s.top();//获取栈顶元素 
w=g.getFirst(x);//栈顶元素对应的第一个关联点 
while(g.getMark(w)==1){//如果w被访问 
w=g.getNext(x,w);
if(w==-1) break;
}
while(w==-1){//没有找到下一个关联点
s.pop();//弹出栈顶元素
x=s.top();
w=g.getFirst(x);
while(g.getMark(w)==1){
w=g.getNext(x,w);
if(w==-1) break;
}
}
s.push(w);
g.setMark(w);
if(w==vg) break;//到达终点
}
while(!s.empty()){
ss.push(s.top());
s.pop();
}
show(g,ss);
}
};

算法结果：

 

算法分析：

根据结果可只知，在有限状态空间下，树搜索不是完备的，图搜索完备；无限状态下不完备。此结果0->1->2->4->6->10->11->12只是其中一条，但不是最优解。

分支因子b，深度d。则最坏情况下时间复杂度也高达空间复杂度  ，内存需求少。

 

 

【迭代加深的深度优先搜索】

基本原理：

迭代加深搜索是以DFS为基础的，它限制DFS递归的层数。

迭代加深搜索的基本步骤是：

1、设置一个固定的深度depth，通常是depth = 1，即只搜索初始状态

2、DFS进行搜索，限制层数为depth，如果找到答案，则结束，如果没有找到答案 则继续下一步

3、如果DFS途中遇到过更深的层，则++depth，并重复2；如果没有遇到，说明搜 索已经结束，没有答案

 

//迭代加深的深度优先搜索类

class IDS{
private:
stack s;
public:
void IDS_Search(Graph g,int v0,int vg,int maxDepth){
for(int i=2;i<=maxDepth;i++){
if(dfsearch(g,v0,vg,i)==1){
break;
}
}
}
int dfsearch(Graph g,int v0,int vg,int maxDepth){
int x,w;
stack ss;
s.push(v0);
g.setMark(v0);
while(true){
x=s.top();
for(w=g.getFirst(x);g.getMark(w)==1;w=g.getNext(x,w)){
if(w==-1)
break;
}
while(w==-1){
s.pop();
if(s.empty()){
g.init();
return 0;
}
x=s.top();
for(w=g.getFirst(x);g.getMark(w)==1;w=g.getNext(x,w)){
if(w==-1)
break;
}
}
s.push(w);
g.setMark(w);
if(w==vg)
break;
if(s.size()>=maxDepth)
s.pop();
}
while(!s.empty()){
ss.push(s.top());
s.pop();
}
show(g,ss);
return 1;
}
};

算法结果：

 

 

算法分析：

因为迭代加深是从按照深度的递增搜索的，所以说0-》1-》2-》4-》7-》12这条 路径，只是在深度最低的情况下找到的结果，并不是最优解。是完备的，时间复杂度也 高达,空间复杂度。

 

 

【广度优先搜索】

基本原理：广度优先搜索，首先从Arad结点出发，判断是否为目标结点，若否，寻找与该结点的邻接点，先搜索该节点的所有子节点，如果子节点没被访问则依次添加到队列，直到找不到子节点，然后出队列获取队列首元素，再搜索该首元素的所有子节点并依次添加到队列。如果找到目标节点则退出循环，否则继续循环。

 

 

 

//广度优先搜索类

class BFS{
private:
list ilist;
stack s,ss;
int pre[20];
public:
BFS(){
for(int i=0;i<20;i++)
pre[i]=-1;
}
void BFS_Search(Graph g,int v0,int vg){
int x,w;//x表示栈顶元素，w表示邻接结点
ilist.push_back(v0);
g.setMark(v0);
while(true){
x=ilist.front();
s.push(x);
ilist.pop_front();
for(w=g.getFirst(x);w!=-1;w=g.getNext(x,w)){
if(g.getMark(w)==1)
continue;
if(w==vg){
pre[w]=x;
break;
}
ilist.push_back(w);
pre[w]=x;
g.setMark(w);
}
if(w==vg){
ilist.push_back(w);
g.setMark(w);
break;
}
}
while(!ilist.empty()){
s.push(ilist.front());
ilist.pop_front();
}
while(!s.empty()){
ss.push(s.top());
s.pop();
}
//计算路径长度 
stack s1=ss,s2=ss,s3=ss;
int result=0;
if(s1.size()==0){
cout<<"路径搜索失败..."<"<"<

算法结果：

 

 

算法分析：

广度优先搜索是层次遍历的，所以说0-》1-》3-》4-》2-》5-》6-》7-》8-》10-》11-》12这条路径，并不是最优解，也不是完备的，它消耗的空间比较大，时间复杂度也高。

 

 

 

【一致代价搜索】

基本原理：

扩展的是路径消耗g(n)最小的节点n,用优先队列来实现，对解的路径步数不关心，只关心路径总代价。即使找到目标节点也不会结束，而是再检查新路径是不是要比老路径好，确实好，则丢弃老路径。

//一致代价搜索类

class UCS{
public:
UCS(Graph g,int v0,int vg){
int pre[20];//用于保存各个节点的前驱节点
int dis[20];//当前节点到起始节点的实际路径长度
for(int i=0;i<20;i++){
pre[i]=-1;
dis[i]=10000;
}
UCS_Search(g,v0,vg,pre,dis);
}
void UCS_Search(Graph g,int v0,int vg,int pre[],int dis[]){
list ilist;
stack s;
ilist.push_back(v0);//添加队列元素 
while(!ilist.empty()){
ilist.sort();
list::iterator it=ilist.begin();
int current=*it;
ilist.erase(it);
g.setMark(current);
if(current==vg)
break;
for(int i=0;i<20;i++){
if(g.getPath(current,i)<10000&&g.getMark(i)==0){
if(!isInlist(i,ilist)){
ilist.push_back(i);
pre[i]=current;
dis[i]=dis[current]+g.getPath(current,i);
}else if(dis[current]+g.getPath(current,i) ilist){
list::iterator it;
for(it=ilist.begin();it!=ilist.end();it++){
if(i==*it){
return true;
}
}
return false;
}
};

算法结果：

 

 

算法分析：

从结果0-》4-》6-》11-》12可以看出。是最优解，他的复杂度不能简单地使用b、d刻画。得使用C*表示最优解的耗散值。时间复杂度，空间复杂度。

 

 

 

【A*搜索】

基本原理：

公式表示为： f(n)=g(n)+h(n),

其中 f(n) 是从初始点经由节点n到目标点的估价函数，

g(n) 是在状态空间中从初始节点到n节点的实际代价，

h(n) 是从n到目标节点最佳路径的估计代价。

保证找到最短路径（最优解的）条件，关键在于估价函数f(n)的选取：

首先将起始结点S放入OPEN表，CLOSE表置空，算法开始时：     

1、如果OPEN表不为空，从表头取一个结点n，如果为空算法失败。     

2、n是目标解吗？是，找到一个解（继续寻找，或终止算法）。     

3、将n的所有后继结点展开，就是从n可以直接关联的结点（子结点），如果不在CLOSE表中，就将它们放入OPEN表，并把S放入CLOSE表，同时计算每一个后继结点的估价值f(n)，将OPEN表按f(x)排序，最小的放在表头，重复算法，回到1。

 

//A*搜索类

class A_Star{
private:
int MaxWeight=10000;
stack s,ss;
public:
void A_Search(Graph g,int v0,int vg,int H[]){
bool flag=true;
int x;//栈顶元素
int vex;//目标节点
int MinF,minVex=v0;//记录最小的f(n)和对应的节点
int GHF[3][20];//分别存储g(n)、h(n)、f(n) 
for(int i=0;i<20;i++){
GHF[0][i]=0;
GHF[2][i]=MaxWeight;
}
s.push(v0);
GHF[0][v0]=0;
GHF[1][v0]=g.getH(v0);
GHF[2][v0]=GHF[0][v0]+GHF[1][v0];
g.setMark(v0);
while(flag){
MinF=MaxWeight;
x=s.top();
vex=g.getFirst(x);
if(vex==vg){
s.push(vex);
g.setMark(vex);
break;
}
if(vex!=-1){
if(g.getMark(vex)==0){
GHF[0][vex]=GHF[0][x]+g.getPath(x,vex);
GHF[1][vex]=g.getH(vex);
GHF[2][vex]=GHF[0][vex]+GHF[1][vex];
if(GHF[2][vex]

实验结果：

 

实验分析：

A*搜索估价值h(n)<= n到目标节点的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低。但能得到最优解。并且如果h(n)=d(n)，即距离估计h(n)等于最短距离，那么搜索将严格沿着最短路径进行，此时的搜索效率是最高的。如果 估价值>实际值,搜索的点数少，搜索范围小，效率高，但不能保证得到最优解。

 

三、算法比较

根据实验结果分析深度优先搜索、迭代加深的深度优先搜索、广度优先搜索以及代价一致搜索、A*搜索算法的时间和空间复杂度。

	完备性	最优解	时间复杂度	空间复杂度
深度优先搜索	否	否	O(b^d)	O(bd)
迭代加深的深度优先搜索	是	是	O(b^d)	O(bd)
广度优先搜索	是	是	O(b^(d+1))	O(b^(d+1))
代价一致搜索	是	是	O(b^[C*/$]	O(b^[C*/$]

 

 

 

【完整代码】

#include
#include
#include
#include
#include
using namespace std;
class Graph{
private:
//城市名
char cities[20][20]={"Arad","Zerind","Oradea","Timisoara","Sibiu","Lugoj",
"Rimnicu Vilcea","Fagaras","Mehadia","Drobeta","Craiova","Pitesti","Bucharest",
"Giurgiu","Urziceni","Hirsova","Eforie","Vaslui","Isi","Neamt"};
int path[20][20]={{0,75,10000,118,140,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{75,0,71,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,71,0,10000,151,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{118,10000,10000,0,10000,111,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{140,10000,151,10000,0,10000,80,99,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,111,10000,0,10000,10000,70,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,80,10000,0,10000,10000,10000,146,97,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,99,10000,10000,0,10000,10000,10000,10000,211,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,70,10000,10000,0,75,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,75,0,120,10000,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,146,10000,10000,120,0,138,10000,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,97,10000,10000,10000,138,0,101,10000,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,211,10000,10000,10000,101,0,90,85,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,90,0,10000,10000,10000,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,85,10000,0,98,10000,142,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,98,0,86,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,86,0,10000,10000,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,142,10000,10000,0,92,10000},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,92,0,87},
{10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,10000,87,0}};
int mark[20];//标志访问函数
//启发式函数
int H[20]={516,524,530,479,403,394,343,326,391,392,310,160,150,155,100,0};
public:
//构造函数
Graph(){
init();
} 
//访问标志初始化
void init(){
for(int i=0;i<20;i++)
mark[i]=0;
}
//第一个孩子 
int getFirst(int start){
if(start>=0 && start<20){
for(int i=0;i<20;i++)
if(path[start][i]>0 && path[start][i]<10000) //表示start和i所表示的点有关系
return i; 
}
return -1;//表示一个孩子也没有 
}
//下一个孩子
int getNext(int start,int w){
if(start>=0 && start<20 && w>=0 && w<20){
for(int i=w+1;i<20;i++)
if(path[start][i]>0 && path[start][i]<10000)//有关联 
return i;
}
return -1;//一个孩子也没有 
}
void setMark(int i){
mark[i]=1;
}
int getMark(int i){
return mark[i];
}
int getH(int i){
return H[i];
}
int* getH(){
return H; 
}
char* getCities(int i){
return cities[i];
}
int getPath(int i,int j){
return path[i][j];
}
};
void show(Graph g,stack s){
stack s1=s,s2=s,s3=s;
int result=0;
if(s1.size()==0){
cout<<"路径搜索失败..."<"<"< s,ss;
public:
void DFS_Search(Graph g,int v0,int vg){
s.push(v0);
g.setMark(v0);
while(true){
x=s.top();//获取栈顶元素 
w=g.getFirst(x);//栈顶元素对应的第一个关联点 
while(g.getMark(w)==1){//如果w被访问 
w=g.getNext(x,w);
if(w==-1) break;
}
while(w==-1){//没有找到下一个关联点
s.pop();//弹出栈顶元素
x=s.top();
w=g.getFirst(x);
while(g.getMark(w)==1){
w=g.getNext(x,w);
if(w==-1) break;
}
}
s.push(w);
g.setMark(w);
if(w==vg) break;//到达终点
}
while(!s.empty()){
ss.push(s.top());
s.pop();
}
show(g,ss);
}
};
//代价一致搜索 
class UCS{
public:
UCS(Graph g,int v0,int vg){
int pre[20];//用于保存各个节点的前驱节点
int dis[20];//当前节点到起始节点的实际路径长度
for(int i=0;i<20;i++){
pre[i]=-1;
dis[i]=10000;
}
UCS_Search(g,v0,vg,pre,dis);
}
void UCS_Search(Graph g,int v0,int vg,int pre[],int dis[]){
list ilist;
stack s;
ilist.push_back(v0);//添加队列元素 
while(!ilist.empty()){
ilist.sort();
list::iterator it=ilist.begin();
int current=*it;
ilist.erase(it);
g.setMark(current);
if(current==vg)
break;
for(int i=0;i<20;i++){
if(g.getPath(current,i)<10000&&g.getMark(i)==0){
if(!isInlist(i,ilist)){
ilist.push_back(i);
pre[i]=current;
dis[i]=dis[current]+g.getPath(current,i);
}else if(dis[current]+g.getPath(current,i) ilist){
list::iterator it;
for(it=ilist.begin();it!=ilist.end();it++){
if(i==*it){
return true;
}
}
return false;
}
};
//迭代加深的深度优先搜索
class IDS{
private:
stack s;
public:
void IDS_Search(Graph g,int v0,int vg,int maxDepth){
for(int i=2;i<=maxDepth;i++){
if(dfsearch(g,v0,vg,i)==1){
break;
}
}
}
int dfsearch(Graph g,int v0,int vg,int maxDepth){
int x,w;
stack ss;
s.push(v0);
g.setMark(v0);
while(true){
x=s.top();
for(w=g.getFirst(x);g.getMark(w)==1;w=g.getNext(x,w)){
if(w==-1)
break;
}
while(w==-1){
s.pop();
if(s.empty()){
g.init();
return 0;
}
x=s.top();
for(w=g.getFirst(x);g.getMark(w)==1;w=g.getNext(x,w)){
if(w==-1)
break;
}
}
s.push(w);
g.setMark(w);
if(w==vg)
break;
if(s.size()>=maxDepth)
s.pop();
}
while(!s.empty()){
ss.push(s.top());
s.pop();
}
show(g,ss);
return 1;
}
};
//A*搜索 
class A_Star{
private:
int MaxWeight=10000;
stack s,ss;
public:
void A_Search(Graph g,int v0,int vg,int H[]){
bool flag=true;
int x;//栈顶元素
int vex;//目标节点
int MinF,minVex=v0;//记录最小的f(n)和对应的节点
int GHF[3][20];//分别存储g(n)、h(n)、f(n) 
for(int i=0;i<20;i++){
GHF[0][i]=0;
GHF[2][i]=MaxWeight;
}
s.push(v0);
GHF[0][v0]=0;
GHF[1][v0]=g.getH(v0);
GHF[2][v0]=GHF[0][v0]+GHF[1][v0];
g.setMark(v0);
while(flag){
MinF=MaxWeight;
x=s.top();
vex=g.getFirst(x);
if(vex==vg){
s.push(vex);
g.setMark(vex);
break;
}
if(vex!=-1){
if(g.getMark(vex)==0){
GHF[0][vex]=GHF[0][x]+g.getPath(x,vex);
GHF[1][vex]=g.getH(vex);
GHF[2][vex]=GHF[0][vex]+GHF[1][vex];
if(GHF[2][vex] ilist;
stack s,ss;
int pre[20];
public:
BFS(){
for(int i=0;i<20;i++)
pre[i]=-1;
}
void BFS_Search(Graph g,int v0,int vg){
int x,w;//x表示栈顶元素，w表示邻接结点
ilist.push_back(v0);
g.setMark(v0);
while(true){
x=ilist.front();
s.push(x);
ilist.pop_front();
for(w=g.getFirst(x);w!=-1;w=g.getNext(x,w)){
if(g.getMark(w)==1)
continue;
if(w==vg){
pre[w]=x;
break;
}
ilist.push_back(w);
pre[w]=x;
g.setMark(w);
}
if(w==vg){
ilist.push_back(w);
g.setMark(w);
break;
}
}
while(!ilist.empty()){
s.push(ilist.front());
ilist.pop_front();
}
while(!s.empty()){
ss.push(s.top());
s.pop();
}
//计算路径长度 
stack s1=ss,s2=ss,s3=ss;
int result=0;
if(s1.size()==0){
cout<<"路径搜索失败..."<"<"<