BAPC2017 Preliminaries (solve6/12)

题目链接：https://nanti.jisuanke.com/?kw=Benelux%20Algorithm%20Programming%20Contest%202017,%20Preliminaries

A题

题意：（对于英语差的我瑟瑟发抖的题意）就给你n个店铺和n个店铺卖的的东西，然后给你一个顺序，问你是否可以从0---n-1商店中递增序列选出来一些店铺可以买到到这些物品，如果购买方案唯一输出什么玩意，没有输出什么玩意，多种方案输出什么玩意。

思路：先将所有物品拍个编号，然后看看那个物品可以在那些店铺购买，然后从前往后匹配，找到满足当前物品的最小编号店铺，然后依次往后，如果找到一条这样的路径的话，在从后往前匹配，找到购买这个物品的最大的编号，然后依次往前找，最后判断2条路是否一样，不一样肯定多条，如果一样肯定单路径。值得一提的是，需要提前判断下购买的物品是否在你查询的商店中出现过，如果没有直接没可能。

#include
using namespace std;
const int maxn=100005;
mapM;   
vectorV[maxn]; //储存一个物品卖的所有商店 
int bian[maxn];     //对于某个物品转换成编号 
int qian[maxn];     //从前边的编号 
int hou[maxn];     //从后边的编号 
int cnt;          //物品排序的编号 
int getid(string s)//将物品编号化 
{
    if(!M.count(s))
        M[s]=cnt++;
    return M[s];
} 
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int n,k,m;
    cin>>n;
    cin>>k;
    for(int i=0;i>num>>s;
        int temp=getid(s);
        V[temp].push_back(num);//卖temp这个物品的商店有那几个 
    }
    for(int i=0;i>m;
    for(int i=0;i>s;
        if(!M.count(s))//出现没卖的物品 
        {
            flag=0;
            break;
        }
        bian[i]=M[s];//名字换算成编号 
    } 
    if(flag==0)
    {
        cout<<"impossible"<=V[id].size())//查无此 
        {
            flag=0;
            break;
        } 
        qian[i]=V[id][temp];//记录下是个店铺 
        pre=V[id][temp];//下次从这个店铺开始 一个店铺可以多买 
    } 
    if(flag==0)
    {
        cout<<"impossible"<=0;i--)
        {
            int id=bian[i];
            int temp=upper_bound(V[id].begin(),V[id].end(),pre)-V[id].begin()-1;//找到一个刚好<=当前店铺 
            hou[i]=V[id][temp];
            pre=V[id][temp]; 
        } 
        int flag=1;
        for(int i=0;i

B题

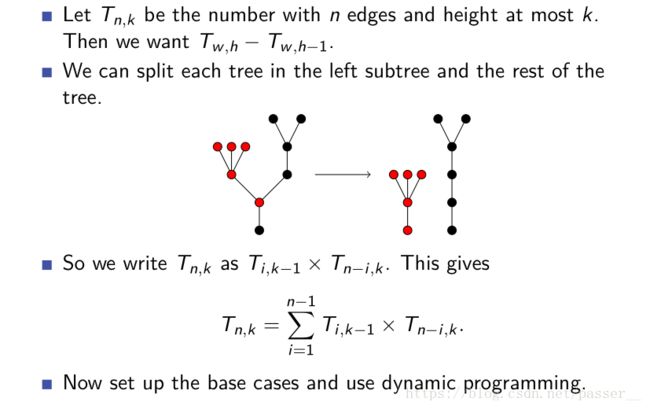
题意：给你h,w。问你可以构建多少不同的盆栽保证高度不超过h,然后边数不超过w.

思想：dp[i][j]代表高度不超过i j条边的方案数。但是去转移呢。

官方题解

：

递推方程为Dp[h][w]=sum( 1<=i<=w   dp[h-1][i]*dp[h][w-i])  因为dp[i][j]是类似前边的一个前缀和

代表分解左右子树，右子树保证高度够，然后枚举左子树的高度，保证高度最大为h-1，这样最高跟右边一样高。

最后需要dp[h][w]-dp[h-1][w]  因为只要高度为h的所以需要减去前边的

#include
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
ll dp[305][305]; 
int main()
{
	int h,w;
	scanf("%d%d",&h,&w);
	for(int i=1;i<=h;i++)//高度小于i的有一个棒的方案 
		dp[i][1]=1;
	for(int i=1;i<=h;i++)
	{
		for(int j=1;j<=w;j++)
		{
			for(int k=1;k<=j-1;k++)
			{
				dp[i][j]=(dp[i][j]+dp[i-1][k]*dp[i][j-k]%mod)%mod;
			} 
		}
	}
	ll ans=(dp[h][w]-dp[h-1][w]+mod)%mod;
	printf("%lld\n",ans);
	return 0;
} 

C题

题意：给你一个城市的n个点之间的图，然后让你找一条从0到n-1的最长单一路（保证唯一），然后问你删除最少的几条边可以满足题意，边号从小到大输出。

思路：Dijkstra算法记录最短路径，然后判断这条路的每个点除了通往最大值的那个边，其余的边标记下，都是需要删掉的，这样就保证了最少的边。

#include
using namespace std;
struct node{
    int v;
    int cost;
    int next;
    int id;
}no[2050];
int head[2005];
int dist[2005];
int pre[2005];
int vis[2005];
int id[2005];//记录id 
int cnt;
void add(int u,int v,int cost,int id)
{
    no[cnt]={v,cost,head[u],id};
    head[u]=cnt++;
}
int main()
{
    memset(head,-1,sizeof(head));   
    cnt=0;
    int n,k;
    cin>>n>>k;
    for(int i=0;iS,S1;
    k=n-1;
    while(k!=0)//将这条路上的边存一下 
    { 
        S.insert(id[k]);
        k=pre[k];
    }
    k=n-1;
    while(k!=-1)
    {
        for(int i=head[k];i!=-1;i=no[i].next)//判断边是不是这条路的边 
        {
            if(!S.count(no[i].id))
                S1.insert(no[i].id);
        }
        k=pre[k];
    }
    int flag=1;
    set::iterator it; 
    for(it=S1.begin(); it!=S1.end();it++)
    {
        if(flag==0)
            cout<<" ";
        cout<<(*it);
        flag=0;
    } 
    if(S1.size()==0)
        cout<<"none"; 
    cout<

D题

题意：刚开始有一个细菌，先让细菌分裂一个小时，然后做n次试验，每次试验需要ai个细菌，如果细菌不够输出error,否则最后输出剩多少细菌mod1e9+7

思想：java模拟过程即可，据说每次乘以2 会T，直接加本身或者左移都不会T，毕竟乘法器最后还需要转换成加法器，多了一个转换过程会变慢。

import java.math.BigInteger;
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        long t;
        t = cin.nextLong();
        int flag=1;
        BigInteger ans = BigInteger.ONE;
        BigInteger temp;
        for (int i = 0; i < t; i++) {
                temp=cin.nextBigInteger();
                ans=ans.add(ans);
                if(ans.compareTo(temp)<0)
                    flag = 0;
                else
                    ans=ans.subtract(temp);
        }
        if(flag==0)
            System.out.println("error");
        else
            System.out.println(ans.mod(BigInteger.valueOf(1000000000+7)));
    }
}

E题

题意：找到一个最小的大于n的数而且是由k个不同2的幂构成的数

思想：k个不同的2的幂的数构成，说明这个数的二进制中1的数量是k个，所以就先考虑n+1中有多少个1，如果>k，就不断让n+(n&(-n))这样减少1，这样会存在一种情况，就是1的个数可能从大于k变成小于k，还需要再次补上，比如（1111这样的会减少）。

#include
using namespace std;
typedef long long ll;
int getbit(ll n)
{
	int ans=0;
	while(n)
	{
		if(n&1)
			ans++;
		n=n>>1;
	} 
	return ans;
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	ll n,k;
	cin>>n>>k;
	n++;
	ll temp=getbit(n);
	if(temp==k)
		cout<k)
		{
			n=n+(n&(-n)); 
		} 
		while(getbit(n)

H题

题意：阅读理解 亚马匹，就是一对情侣在1百万天内看电影，如果对于一部电影都喜欢那肯定去看，如果有一个人喜欢的话，那么看了这个下次必须看对方喜欢的电影。

思路：模拟下就好了。

#include
using namespace std;
typedef long long ll;
const int maxn = 1000005;
int a[maxn];
int b[maxn];
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
	int n,m;
	cin>>n;
	for(int i=0;i>temp;
		a[temp]=1;
	}
	cin>>m; 
	for(int i=0;i>temp;
		b[temp]=1;
	}
	int ans=0;
	int flag1=0,flag2=0;
	for(int i=0;i