机器学习 | 吴恩达机器学习第八周编程作业(Python版）

实验指导书    下载密码:963j

本篇博客主要讲解，吴恩达机器学习第八周的编程作业，主要包含KMeans实验和PCA实验两部分。原始实验使用Matlab实现，本篇博客提供Python版本。

目录

1.实验包含的文件

2.KMeans实验

3.K-means实验完整代码

4.PCA实验

5.PCA实验完整代码

---

1.实验包含的文件

文件名称	含义
ex7.py	K-means实验主程序
ex7_pca.py	PCA实验主程序
ex7data1.mat	PCA实验数据集
ex7data2.mat	K-means实验数据集
ex7faces.mat	人脸数据集
bird_small.png	示例图片
displayData.py	可视化数据
runkMeans.py	运行K-means算法
pca.py	运行PCA
projectData.py	将原始数据映射到低维空间
recoverData.py	将压缩数据恢复到原始数据
findClosestCentroids.py	找到最近的簇
computeCentroids.py	更新聚类中心
kMeansInitCentroids.py	初始化k-means的初始聚类中心

完成红色部分程序的关键代码。

2.KMeans实验

• 打开KMeans实验主程序ex7.py

'''第1部分 为每个样本点找到离他最近的聚类中心'''

print('Finding closest centroids.')

data = scio.loadmat('ex7data2.mat') #加载矩阵格式的数据
X = data['X']  #提取输入特征矩阵


k = 3  # 随机初始化3个聚类中心
initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])

#找到离每个样本最近的初始聚类中心序号
idx = fc.find_closest_centroids(X, initial_centroids)

print('Closest centroids for the first 3 examples: ')
print('{}'.format(idx[0:3]))
print('(the closest centroids should be 0, 2, 1 respectively)')

• 编写findClosestCentroids.py  簇分配

def find_closest_centroids(X, centroids):
    
    K = centroids.shape[0]  #聚类中心数量

    m = X.shape[0]  #样本数

  
    idx = np.zeros(m) #存储m个样本对应的最近的聚类中心序号

    for i in range(m):
        a=(X[i]-centroids).dot((X[i]-centroids).T)  #得到一个方阵  对角线上的元素为该样本点到每个聚类中心的距离
        idx[i]=np.argsort(a.diagonal())[0]  #取出对角线元素 对其索引进行排序  返回离该样本最近的聚类中心的序号

    return idx

验证正确性：

• 更新聚类中心

'''第2部分 更新聚类中心'''

print('Computing centroids means.')

centroids = cc.compute_centroids(X, idx, k) #在簇分配结束后 对每个簇的样本点重新计算聚类中心

print('Centroids computed after initial finding of closest centroids: \n{}'.format(centroids))
print('the centroids should be')
print('[[ 2.428301 3.157924 ]')
print(' [ 5.813503 2.633656 ]')
print(' [ 7.119387 3.616684 ]]')

• 编写computeCentroids.py

def compute_centroids(X, idx, K):
   
    (m, n) = X.shape #m为样本数 n为每个样本的特征数

    centroids = np.zeros((K, n)) #存储新的聚类中心的位置 

    for i in range(K):
        centroids[i]=np.mean(X[idx==i],axis=0)   #对每个簇 计算新的聚类中心 axis=0对每一列求均值

    return centroids

验证正确性：

• 运行k-means算法

'''第3部分 运行k-means聚类算法'''
print('Running K-Means Clustering on example dataset.')

#加载数据集
data = scio.loadmat('ex7data2.mat') 
X = data['X']


K = 3   #聚类中心数量
max_iters = 10  #设置外循环迭代次数

initial_centroids = np.array([[3, 3], [6, 2], [8, 5]])  #初始化聚类中心

centroids, idx = km.run_kmeans(X, initial_centroids, max_iters, True) #运行k-means算法 返回最终聚类中心位置即每个样本点所属的聚类中心
#并把中间过程以及最终聚类效果可视化
print('K-Means Done.')

• 查看runKMeans.py

def run_kmeans(X, initial_centroids, max_iters, plot): #plot设置是否进行可视化 
    if plot:
        plt.figure()

    (m, n) = X.shape #m样本数  n样本特征数
    K = initial_centroids.shape[0]  #聚类中心数量
    centroids = initial_centroids
    previous_centroids = centroids
    idx = np.zeros(m)  #存放每个样本所属的聚类中心序号

    # 运行k-means
    for i in range(max_iters):  #外循环
        print('K-Means iteration {}/{}'.format((i + 1), max_iters))  

        idx = fc.find_closest_centroids(X, centroids) #第一个内循环 为每个样本找到最近的聚类中心
        
        if plot:
            plot_progress(X, centroids, previous_centroids, idx, K, i) #画出此时簇分配的状态
            previous_centroids = centroids
            input('Press ENTER to continue')

        centroids = cc.compute_centroids(X, idx, K) #第2个内循环  更新聚类中心

    return centroids, idx  #返回最终聚类中心的位置  和每个样本所属的聚类中心序号


def plot_progress(X, centroids, previous, idx, K, i):
    plt.scatter(X[:, 0], X[:, 1], c=idx, s=15)   #不同聚类中心用不同的颜色表示 

    plt.scatter(centroids[:, 0], centroids[:, 1], marker='x', c='black', s=25) #标出聚类中心

    for j in range(centroids.shape[0]):  #为更新后的聚类中心和之前的聚类中心连线
        draw_line(centroids[j], previous[j])

    plt.title('Iteration number {}'.format(i + 1))


def draw_line(p1, p2):
    plt.plot(np.array([p1[0], p2[0]]), np.array([p1[1], p2[1]]), c='black', linewidth=1)

• 最终的聚类效果和聚类中心的移动过程

• 使用k-means压缩图片

'''第4部分 运行k-means聚类算法 压缩图片'''
print('Running K-Means clustering on pixels from an image')

#加载图片
image = io.imread('bird_small.png')
image = img_as_float(image)

# 图片大小
img_shape = image.shape


X = image.reshape(img_shape[0] * img_shape[1], 3) #把图片转换成3个列向量构成的矩阵  每个列向量代表每个颜色通道的所有像素点 

#可以设置不同的参数 观察效果
K = 16 #聚类中心数量
max_iters = 10 #外循环迭代次数

#初始化聚类中心位置很重要  初始化不同  最终聚类效果也会不同
initial_centroids = kmic.kmeans_init_centroids(X, K) 

# 运行k-means
centroids, idx = km.run_kmeans(X, initial_centroids, max_iters, False) #False不进行可视化

print('K-Means Done.')

input('Program paused. Press ENTER to continue')


print('Applying K-Means to compress an image.')

# 得到最终聚类结束后 每个样本所属的聚类中心序号
idx = fc.find_closest_centroids(X, centroids)

#用idx做索引
idx=idx.astype(int) #将数值类型转换为整型
idx=idx.tolist()  #将数组转换为列表  

X_recovered = centroids[idx]  #将每个样本点位置转换为它所属簇的聚类中心的位置  实现压缩

X_recovered = np.reshape(X_recovered, (img_shape[0], img_shape[1], 3)) #把图像转换为之前的维度

io.imsave('compress.png',X_recovered) #保存压缩后的图片文件
plt.subplot(2, 1, 1)  #可视化原始图片
plt.imshow(image)
plt.title('Original')

plt.subplot(2, 1, 2)  #压缩后的图片
plt.imshow(X_recovered)
plt.title('Compressed, with {} colors'.format(K))

input('ex7 Finished. Press ENTER to exit')

• 编写kMeansInitCentroids.py 

def kmeans_init_centroids(X, K):
    #随机初始化聚类中心
    centroids = np.zeros((K, X.shape[1]))  

    #初始化聚类中心为数据集中的样本点
    centroids=X[np.random.randint(0,X.shape[0],K)]

    return centroids

• 图片压缩效果

3.K-means实验完整代码

下载链接   下载密码:rqk6

4.PCA实验

• 打开PCA实验主程序ex7_pca.py

'''第1部分 加载数据集 并可视化'''
#小数据集方便可视化
print('Visualizing example dataset for PCA.')

data = scio.loadmat('ex7data1.mat')
X = data['X'] #两个特征 

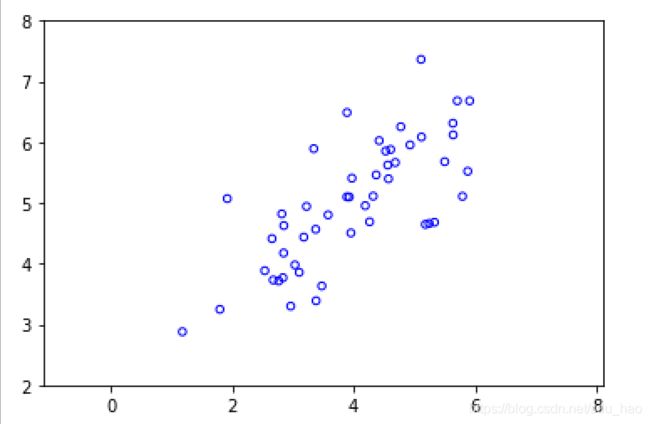
# 可视化
plt.figure()
plt.scatter(X[:, 0], X[:, 1], facecolors='none', edgecolors='b', s=20)
plt.axis('equal')
plt.axis([0.5, 6.5, 2, 8])

• 可视化效果

• 实现PCA算法

'''第2部分 实现PCA 进行数据压缩'''

print('Running PCA on example dataset.')

# 在PCA之前 要对特征进行缩放
X_norm, mu, sigma = fn.feature_normalize(X)

# 执行PCA 返回U矩阵  和S矩阵
U, S = pca.pca(X_norm)

#对比两个不同的特征向量 U[:,0]更好 投影误差最小  U中的各个特征向量（列）都是正交的  2D->1D 取前1个特征向量 作为Ureduce
rk.draw_line(mu, mu + 1.5 * S[0] * U[:, 0]) 
rk.draw_line(mu, mu + 1.5 * S[1] * U[:, 1])

print('Top eigenvector: \nU[:, 0] = {}'.format(U[:, 0])) #利用PCA得到的特征向量矩阵Ureduce（降维后子空间的基）
print('You should expect to see [-0.707107 -0.707107]')

• 查看特征缩放程序featureNormalize.py

def feature_normalize(X):
    mu = np.mean(X, 0)  #对特征矩阵每一列求均值
    sigma = np.std(X, 0, ddof=1)  #特征矩阵每一列求标准差
    X_norm = (X - mu) / sigma  #特征矩阵每一列的元素减去该列均值  除以该列标准差  得到特征缩放后的矩阵

    return X_norm, mu, sigma

• 编写pca.py

def pca(X):
   
    (m, n) = X.shape  #m 样本数  n特征数

    U = np.zeros((n,n)) #U 为n*n的矩阵
    S = np.zeros(n)  #S也是n*n的对角矩阵  只不过svd返回的是其对角线的非0元素 
    #计算协方差矩阵
    Sigma=(1/m)*(X.T.dot(X))
    #对协方差矩阵进行奇异值分解
    U,S,V=scipy.linalg.svd(Sigma)
   
    return U, S

• 可视化降维后的特征向量（子空间的基向量）

验证程序正确性：

• 得到降维后的样本点并进行压缩重放

'''第3部分 得到降维后的样本点 再进行压缩重放'''
print('Dimension reductino on example dataset.')

# 可视化特征缩放后的数据集
plt.figure()
plt.scatter(X_norm[:, 0], X_norm[:, 1], facecolors='none', edgecolors='b', s=20)
plt.axis('equal')
plt.axis([-4, 3, -4, 3])

# 将2维数据映射到1维
K = 1
Z = pd.project_data(X_norm, U, K)
print('Projection of the first example: {}'.format(Z[0]))
print('(this value should be about 1.481274)')

X_rec = rd.recover_data(Z, U, K) #将降维后的1维数据 转换为2维（在特征向量上的投影点）

print('Approximation of the first example: {}'.format(X_rec[0]))
print('(this value should be about [-1.047419 -1.047419])')

# 画出特征缩放后的样本在特征向量上的投影点 并在2者之间连线
plt.scatter(X_rec[:, 0], X_rec[:, 1], facecolors='none', edgecolors='r', s=20)
for i in range(X_norm.shape[0]):
    rk.draw_line(X_norm[i], X_rec[i])

• 编写降维程序projectData.py

def project_data(X, U, K): #得到降维后的样本点

    Z = np.zeros((X.shape[0], K)) #降维后的特征矩阵 Z：m*K X：m*n

    Z=X.dot(U[:,:K])

    return Z

• 编写压缩重放程序recoverData.py

def recover_data(Z, U, K):  #进行压缩重放
    
    X_rec = np.zeros((Z.shape[0], U.shape[0])) #原始样本在特征向量上的投影点 X_rec:m*n Z:m*K  U:n*n

    X_rec=Z.dot(U[:,:K].T)

    return X_rec

• 可视化效果

验证程序正确性：

• 加载并可视化人脸数据

'''第4部分 加载并可视化人脸数据集'''

print('Loading face dataset.')

data = scio.loadmat('ex7faces.mat')
X = data['X'] #得到输入特征矩阵  
print(X.shape[1]) #特征为1024维
disp.display_data(X[0:100]) #可视化前100个人脸

• 可视化效果

• 可视化人脸数据的特征向量

'''第5部分 可视化人脸数据的特征向量'''
print('Running PCA on face dataset.\n(this might take a minute or two ...)')

X_norm, mu, sigma = fn.feature_normalize(X) #对输入特征矩阵进行特征缩放

#执行PCA算法
U, S = pca.pca(X_norm)

#可视化前36个特征向量（每个向量1024维）
disp.display_data(U[:, 0:36].T)

• 可视化效果

• 对人脸数据进行降维（1024->100)

'''第6部分 对人脸数据进行降维 从1024维降到100维'''
print('Dimension reduction for face dataset.')

K = 100
Z = pd.project_data(X_norm, U, K)  #得到降维后的特征矩阵（样本点）

print('The projected data Z has a shape of: {}'.format(Z.shape)) #m*100

• 可视化降维后，再压缩重放后的人脸数据与原数据比较

'''第7部分 可视化降维后,再压缩重放的人脸数据和原始数据比较'''
print('Visualizing the projected (reduced dimension) faces.')

K = 100
X_rec = rd.recover_data(Z, U, K) #压缩重放

#可视化原始数据
disp.display_data(X_norm[0:100])
plt.title('Original faces')
plt.axis('equal')

#压缩到100维  再压缩重放后的数据
disp.display_data(X_rec[0:100])
plt.title('Recovered faces')
plt.axis('equal')

PCA要求投影误差最小，所以2者应该是差不多的：

• 利用PCA可视化高维数据

PCA可以把高维数据降至低维再进行可视化：

'''第8部分 利用PCA可视化高维数据'''
image = io.imread('bird_small.png') #读取图片
image = img_as_float(image)

img_shape = image.shape

X = image.reshape((img_shape[0] * img_shape[1], 3))  #将图片格式转换为包含3列（3个颜色通道）的矩阵
K = 16   #聚类中心数量
max_iters = 10  #外循环迭代次数
initial_centroids = kmic.kmeans_init_centroids(X, K)  #初始化K个聚类中心
centroids, idx = km.run_kmeans(X, initial_centroids, max_iters, False) #执行k-means，得到最终的聚类中心和每个样本点所属的聚类中心序号


selected = np.random.randint(X.shape[0], size=1000) #随机选择1000（可以更改）个样本点 每个样本点3维

#可视化3维数据  不同颜色表示每个样本点的所属的簇
cm = plt.cm.get_cmap('RdYlBu')
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[selected, 0], X[selected, 1], X[selected, 2], c=idx[selected],cmap=cm, s=15, vmin=0, vmax=K)
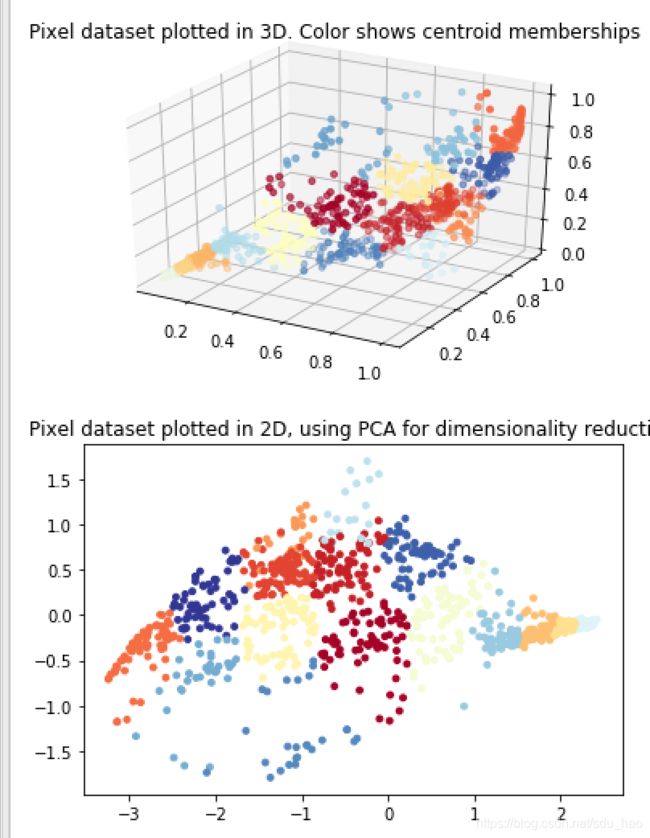
plt.title('Pixel dataset plotted in 3D. Color shows centroid memberships')

input('Program paused. Press ENTER to continue')

#利用PCA把3维数据 降至2维 进行可视化

X_norm, mu, sigma = fn.feature_normalize(X)  #对特征矩阵X 进行特征缩放

#调用pca 3D->2D
U, S = pca.pca(X_norm)
Z = pd.project_data(X_norm, U, 2)  #得到降维后的特征矩阵

# 可视化2维数据  不同颜色表示每个样本点的所属的簇
plt.figure()
plt.scatter(Z[selected, 0], Z[selected, 1], c=idx[selected].astype(np.float64), cmap=cm,s=15)
plt.title('Pixel dataset plotted in 2D, using PCA for dimensionality reduction')

• 可视化效果

5.PCA实验完整代码

下载链接