21、多项式插值,最小二乘法和牛顿迭代法
1、多项式插值
利用函数f (x)在某区间中已知的若干点的函数值,作出适当的特定函数,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方法称为插值法。如果这特定函数是多项式,就称它为插值多项式。
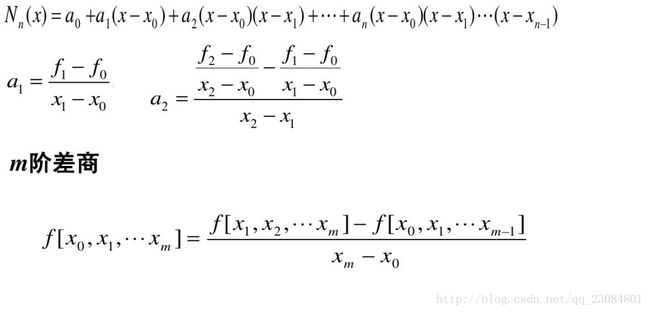
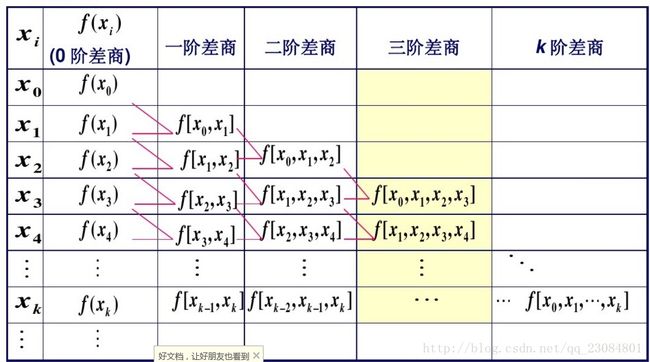
//*x、*fx分别为已知点数组(x0,f(x0))..(xn,f(xn));n为已知点个数
// *z、*fz分别为待求点数组(z0,f(z0))..(zn,f(zn));m为待求点个数
int interpol(const double *x, const double *fx, int n, double *z, double *pz, int m)
{
double term, *table, *coeff;
int i, j ,k;
//table存临时差商,每组从一阶到n阶更新,对应上图的每行更新 ,
//如 [x0 x1],[x1x2],...,[xn-1 xn];更新到[x0 x1 x2],...,[xn-2, xn-1, xn]
//coeff存最终差商 ,机每次取table更新的第一项,如[x0 x1]到[x0 x1...xn]
if((table = (double *)malloc(sizeof(double) * n)) == NULL)
return -1;
if((coeff = (double *)malloc(sizeof(double) * n)) == NULL)
{
free(table);
return -1;
}
memcpy(table, fx, sizeof(double) * n);
coeff[0] = table[0];
//k对应行
for(k = 1; k < n; k++)
{
//第k行只有n-k个差商
for(i = 0;i < n - k; i++)
{
table[i] = (table[i + 1] - table[i]) / (x[i + k] -x[i])
}
//我们要的差商只是每行第一个即[x0 x1],...,[x0,x1,...,xn]
coeff[k] = table[0];
}
free(table);
//求m个未知点
for(k = 0;k < m; k++)
{
pz[k] = coeff[0];
//j对应公式中每个加数的长度。
for(j = 1; j < n; j++)
{
term = coeff[j];
//下面term为第j个加数对应的an(x-x0)(x-x1)...(x-xn-1) ,需要累乘
for(i = 0; i < j; i++)
term = term * (z[k] - x[i]);
//把这些加数都加起来
pz[k] = pz[k] + term;
}
}
free(coeff);
return 0;
}2、最小二乘估计法
最小二乘法(又称最小平方法)通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。就是求一条线到所有点距离(x相同y的差值)都近。

//*x,*y对应已知的坐标数组;n为已知点个数;a、b为待求方程y = a + bx的系数
void lsqe(const double *x, const double *y, int n, double n, double *b, double *a)
{
//sumx2位xi的平方和
double sumx, sumy, sumx2, sumxy;
int i;
sumx = 0.0;
sumy = 0.0;
sumxy = 0.0;
sumx2 = 0.0;
for(i = 0; i < n; i++)
{
sumx = sumx + x[i];
sumy = sumy + y[i];
sumx2 = sumx2 + pow(x[i],2);
sumxy = sumxy +(x[i] * y[i]);
}
*b = (sumxy -(sumx * sumy) / (double)n) / (sumx2 - (pow(sumx, 2.0) / (double)n));
*a = (sumy - (*b) * sumx) / (double)n;
return;
}3、牛顿迭代法
1、牛顿迭代法通过一系列操作使得结果不断逼近方程的实根。

2、1阶导数表示单调性,2阶导数表示凹凸性。x0的选择要求:(1)x0在[a b]内只有一个跟;(2)x0=a或者x0=b时f(x0)和二阶导数 在[a b]上符号相同。这样保证每次迭代逐步逼近。
//g(x)为f(x)的导数,x为数组存放每次迭代的数,n为最大迭代次数或最终迭代次数,delta为允许误差
int root(double (*f)(double x), double (*g)(double *x), double *x, int *n, double delta)
{
int satisfied, i;
i = 0;
satisfied = 0;
while(!satisfied && i+1 < *n)
{
x[i+1] = x[i] - (f(x[i]) / g(x[i]));
if(fabs(x[i+1] - x[i]) < delta)
satisfied = 1;
i++;
}
//如果没有达到最大迭代次数就符合要求,使n等于此时的迭代次数
if(i == 0)
*n = 1;
else
*n = i + 1;
if(satisfied)
return 0;
else
return -1;
}