数据结构与算法：38 | 分治算法：归并排序的巧用

如何理解分治算法？

分治算法（divide and conquer）的核心思想就是四个字，分而治之 ，将原问题划分成 n 个规模较小，并且结构与原问题相似的子问题，递归地解决这些子问题，再合并其结果，就得到原问题的解。

这个定义看起来类似递归的定义。关于分治和递归的区别，排序的时候讲过，分治算法是一种处理问题的思想，递归是一种编程技巧。实际上，分治算法一般都比较适合用递归来实现。分治算法的递归实现中，每一层递归都会涉及这样三个操作：

• 分解：将原问题分解成一系列子问题；
• 解决：递归地求解各个子问题，若子问题足够小，则直接求解；
• 合并：将子问题的结果合并成原问题。

分治算法能解决的问题，一般满足下面几个条件：

• 原问题与分解的小问题具有相同模式；
• 原问题分解的子问题可以独立求解，子问题之间没有相关性，这一点是分治算法跟动态规划的明显区别；
• 具有分解终止条件，当问题足够小时，可以直接求解；
• 可以将子问题合并成原问题，合并操作的复杂度不能太高，否则就起不到减小算法总体复杂度的效果了。

分治算法应用举例分析

理解分治算法的原理并不难，但是要想灵活应用并不容易。所以，接下来，我会带你用分治算法解决讲排序的时候涉及的一个问题，加深你对分治算法的理解。

还记得排序算法里的数据的有序度、逆序度的概念吗？我们用有序度来表示一组数据的有序程度，用逆序度表示一组数据的无序程度。

假设有 n 个数据，从小到大排列，那完全有序的数据的有序度就是 n(n-1)/2，逆序度等于 0；相反，倒序排列的数据的有序度就是 0，逆序度是 n(n-1)/2。除了这两种极端情况外，我们可以通过计算有序对或者逆序对的个数，来表示数据的有序度或逆序度。

现在的问题是，如何编程求出一组数据的有序对个数或者逆序对个数呢？因为有序对个数和逆序对个数的求解方式是类似的（逆序度 = 满有序度 - 有序度），所以你可以只思考逆序对个数的求解方法。

最笨的方法是，拿每个数字跟它后面的数字比较，看有几个比它小的。两层for循环，时间复杂度是 O(n^2)。那有没有更加高效的处理方法呢？

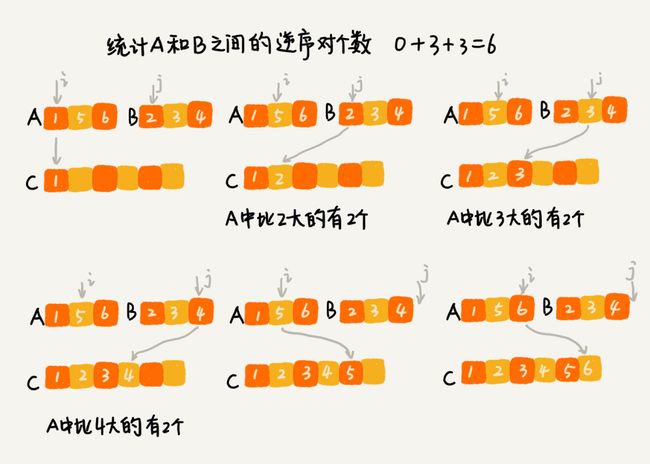
我们用分治算法来试试。套用分治的思想来求数组 A 的逆序对个数。可以将数组分成前后两半 A1 和 A2，分别计算 A1 和 A2 的逆序对个数 K1 和 K2，然后再计算 A1 与 A2 之间的逆序对个数 K3。那数组 A 的逆序对个数就等于 K1+K2+K3。

前面讲过，使用分治算法一个要求是，子问题合并的代价不能太大，否则就起不了降低时间复杂度的效果。那回到这个问题，如何快速计算出两个子问题 A1 与 A2 之间的逆序对个数呢？

这里就要借助归并排序算法了。你可以先试着想想，如何借助归并排序算法来解决呢？

归并排序中有一个非常关键的操作，将两个有序的小数组，合并成一个有序的数组。实际上，在合并过程中，就可以计算这两个小数组的逆序对个数。每次合并操作，都计算一次逆序对个数，把这些计算出来的逆序对个数求和，就是这个数组的逆序对个数。

把这个过程翻译成了代码：

private int num = 0; // 全局变量或者成员变量

public int count(int[] a, int n) {
    num = 0;
    mergeSortCounting(a, 0, n-1);
    return num;
}

private void mergeSortCounting(int[] a, int p, int r) {
    if (p >= r) return;
    int q = (p+r)/2;
    mergeSortCounting(a, p, q);
    mergeSortCounting(a, q+1, r);
    merge(a, p, q, r);
}

private void merge(int[] a, int p, int q, int r) {
    int i = p, j = q+1, k = 0;
    int[] tmp = new int[r-p+1];
    while (i<=q && j<=r) {
        if (a[i] <= a[j]) 
            tmp[k++] = a[i++];
        else {
            num += (q-i+1); // 统计p-q之间，比a[j]大的元素个数
            tmp[k++] = a[j++];
        }
    }
    while (i <= q)// 处理剩下的
        tmp[k++] = a[i++];
    while (j <= r) // 处理剩下的
        tmp[k++] = a[j++];
    for (i = 0; i <= r-p; ++i) // 从tmp拷贝回a
        a[p+i] = tmp[i];
}

这个问题，并不是每个人都能想到可以借助归并排序算法来解决，不夸张地说，如果之前没接触过，绝大部分人都想不到。但是，如果我告诉你可以借助归并排序算法来解决，那你就应该要想到如何改造归并排序，来求解这个问题了，只要你能做到这一点，我觉得就很棒了。

具体例子看这个：

剑指 Offer 51. 数组中的逆序对 - 力扣（LeetCode）
LeetCode第 327 题：区间和的个数(C++)_qq_32523711的博客-CSDN博客
LeetCode第 493 题：翻转对(C++)_qq_32523711的博客-CSDN博客
LeetCode第 315 题：计算右侧小于当前元素的个数(C++)_qq_32523711的博客

分治思想在海量数据处理中的应用

分治算法思想的应用是非常广泛的，不仅限于指导编程和算法设计。还经常用在海量数据处理的场景中。我们前面讲的数据结构和算法，大部分都是基于内存存储和单机处理。但是，如果要处理的数据量非常大，没法一次性放到内存中，这个时候，这些数据结构和算法就无法工作了。

比如，给 10GB 的订单文件按照金额排序这样一个需求，看似是一个简单的排序问题，但是因为数据量大，有 10GB，而我们的机器的内存可能只有 2、3GB 这样子，无法一次性加载到内存，也就无法通过单纯地使用快排、归并等基础算法来解决了。

要解决这种数据量大到内存装不下的问题，就可以利用分治的思想。可以将海量的数据集合根据某种方法，划分为几个小的数据集合，每个小的数据集合单独加载到内存来解决，然后再将小数据集合合并成大数据集合。实际上，利用这种分治的处理思路，不仅仅能克服内存的限制，还能利用多线程或者多机处理，加快处理的速度。

比如刚刚举的那个例子，给 10GB 的订单排序，我们就可以先扫描一遍订单，根据订单的金额，将 10GB 的文件划分为几个金额区间。比如订单金额为 1 到 100 元的放到一个小文件，101 到 200 之间的放到另一个文件，以此类推。这样每个小文件都可以单独加载到内存排序，最后将这些有序的小文件合并，就是最终有序的 10GB 订单数据了。

如果订单数据存储在类似 GFS 这样的分布式系统上，当 10GB 的订单被划分成多个小文件的时候，每个文件可以并行加载到多台机器上处理，最后再将结果合并在一起，这样并行处理的速度也加快了很多。不过，这里有一个点要注意，就是数据的存储与计算所在的机器是同一个或者在网络中靠的很近（比如一个局域网内，数据存取速度很快），否则就会因为数据访问的速度，导致整个处理过程不但不会变快，反而有可能变慢。