吴恩达深度学习第一课第四周课后作业1参考
**第四周课后作业第一部分,对于作业环境安装不知道的可以看一下这里:
http://blog.csdn.net/liuzhongkai123/article/details/78766351
**
Building your Deep Neural Network: Step by Step
符号说明
Notation:
- Superscript [l] denotes a quantity associated with the lth layer.
- Example: a[L] is the Lth layer activation. W[L] and b[L] are the Lth layer parameters.
- Superscript (i) denotes a quantity associated with the ith example.
- Example: x(i) is the ith training example.
- Lowerscript i denotes the ith entry of a vector.
- Example: a[l]i denotes the ith entry of the lth layer’s activations).
1 - Packages
导入被作业需要的包和模块
Let’s first import all the packages that you will need during this assignment.
- numpy is the main package for scientific computing with Python.
- matplotlib is a library to plot graphs in Python.
- dnn_utils provides some necessary functions for this notebook.
- testCases provides some test cases to assess the correctness of your functions
- np.random.seed(1) is used to keep all the random function calls consistent. It will help us grade your work. Please don’t change the seed.
导入包和模块
import numpy as np
import h5py
import matplotlib.pyplot as plt
from testCases_v2 import *
from testCases_v3 import *
from dnn_utils_v2 import sigmoid, sigmoid_backward, relu, relu_backward设置绘图配置文件参数
%matplotlib inline 设置绘图的配置文件
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'设置随机数种子,保证随数的连续
np.random.seed(1) #设置随机数种子2 - Outline of the Assignment
To build your neural network, you will be implementing several “helper functions”. These helper functions will be used in the next assignment to build a two-layer neural network and an L-layer neural network. Each small helper function you will implement will have detailed instructions that will walk you through the necessary steps. Here is an outline of this assignment, you will:
- Initialize the parameters for a two-layer network and for an L-layer neural network.
Implement the forward propagation module (shown in purple in the figure below).
- Complete the LINEAR part of a layer’s forward propagation step (resulting in Z[l] ).
- We give you the ACTIVATION function (relu/sigmoid).
- Combine the previous two steps into a new [LINEAR->ACTIVATION] forward function.
- Stack the [LINEAR->RELU] forward function L-1 time (for layers 1 through L-1) and add a [LINEAR->SIGMOID] at the end (for the final layer L). This gives you a new L_model_forward function.
Compute the loss.
Implement the backward propagation module (denoted in red in the figure below).
- Complete the LINEAR part of a layer’s backward propagation step.
- We give you the gradient of the ACTIVATE function (relu_backward/sigmoid_backward)
- Combine the previous two steps into a new [LINEAR->ACTIVATION] backward function.
- Stack [LINEAR->RELU] backward L-1 times and add [LINEAR->SIGMOID] backward in a new L_model_backward function
Finally update the parameters.
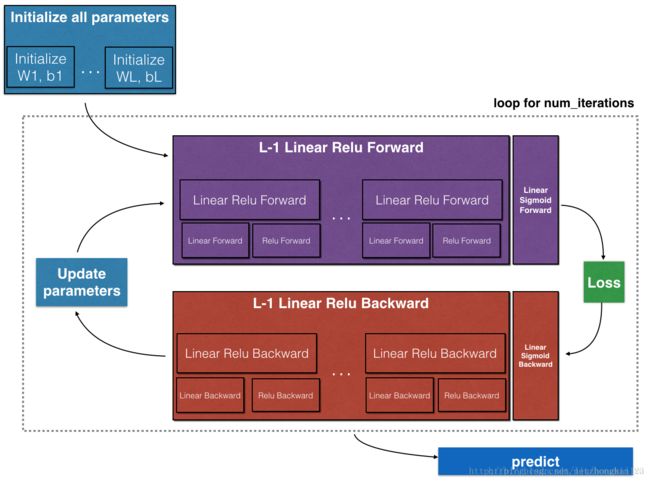
Note that for every forward function, there is a corresponding backward function. That is why at every step of your forward module you will be storing some values in a cache. The cached values are useful for computing gradients. In the backpropagation module you will then use the cache to calculate the gradients. This assignment will show you exactly how to carry out each of these steps.
3 - Initialization
You will write two helper functions that will initialize the parameters for your model. The first function will be used to initialize parameters for a two layer model. The second one will generalize this initialization process to L layers.
3.1 - 2-layer Neural Network
Exercise: Create and initialize the parameters of the 2-layer neural network.
Instructions:
- The model’s structure is: LINEAR -> RELU -> LINEAR -> SIGMOID.
- Use random initialization for the weight matrices. Use np.random.randn(shape)∗0.01 with the correct shape.
- Use zero initialization for the biases. Use np.zeros(shape) .
定义初始化函数
def initialize_parameters(n_x,n_h,n_y):
np.random.seed(1) #没有这句得不到预期结果
W1=np.random.randn(n_h,n_x)*0.01
b1=np.zeros((n_h,1))
W2=np.random.randn(n_y,n_h)*0.01
b2=np.zeros((n_y,1))
assert(W1.shape==(n_h,n_x))
assert(b1.shape==(n_h,1))
assert(W2.shape==(n_y,n_h))
assert(b2.shape==(n_y,1))
parameters={'W1':W1,
'b1':b1,
'W2':W2,
'b2':b2}
return parameters测试:
parameters = initialize_parameters(2,2,1)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))结果:
W1 = [[ 0.01624345 -0.00611756]
[-0.00528172 -0.01072969]]
b1 = [[ 0.]
[ 0.]]
W2 = [[ 0.00865408 -0.02301539]]
b2 = [[ 0.]]3.2 - L-layer Neural Network
The initialization for a deeper L-layer neural network is more complicated because there are many more weight matrices and bias vectors. When completing the initialize_parameters_deep, you should make sure that your dimensions match between each layer. Recall that n[l] is the number of units in layer l. Thus for example if the size of our input X is (12288,209) (with m=209 examples) then:

Remember that when we compute WX+b in python, it carries out broadcasting. For example, if:
Then WX+b will be:
Exercise: Implement initialization for an L-layer Neural Network.
Instructions:
- The model’s structure is [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID. I.e., it has L−1 layers using a ReLU activation function followed by an output layer with a sigmoid activation function.
- Use random initialization for the weight matrices. Use np.random.rand(shape) * 0.01.
- Use zeros initialization for the biases. Use np.zeros(shape).
- We will store n[l] , the number of units in different layers, in a variable layer_dims. For example, the layer_dims for the “Planar Data classification model” from last week would have been [2,4,1]: There were two inputs, one hidden layer with 4 hidden units, and an output layer with 1 output unit. Thus means W1’s shape was (4,2), b1 was (4,1), W2 was (1,4) and b2 was (1,1). Now you will generalize this to L layers!
- Here is the implementation for L=1 (one layer neural network). It should inspire you to implement the general case (L-layer neural network).
参数初始化函数:
def initialize_parameters_deep(layer_dims):
np.random.seed(3)
parameters={}
L=len(layer_dims)
for l in range(1,L):
parameters['W' + str(l)]=np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
parameters['b' + str(l)]=np.zeros((layer_dims[l],1))
assert(parameters['W' + str(l)].shape==(layer_dims[l],layer_dims[l-1]))
assert(parameters['b' + str(l)].shape==(layer_dims[l],1))
return parameters测试:
parameters = initialize_parameters_deep([5,4,3])
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))结果:
W1 = [[ 0.01788628 0.0043651 0.00096497 -0.01863493 -0.00277388]
[-0.00354759 -0.00082741 -0.00627001 -0.00043818 -0.00477218]
[-0.01313865 0.00884622 0.00881318 0.01709573 0.00050034]
[-0.00404677 -0.0054536 -0.01546477 0.00982367 -0.01101068]]
b1 = [[ 0.]
[ 0.]
[ 0.]
[ 0.]]
W2 = [[-0.01185047 -0.0020565 0.01486148 0.00236716]
[-0.01023785 -0.00712993 0.00625245 -0.00160513]
[-0.00768836 -0.00230031 0.00745056 0.01976111]]
b2 = [[ 0.]
[ 0.]
[ 0.]]4 - Forward propagation module
4.1 - Linear Forward
前向传播线性函数
Now that you have initialized your parameters, you will do the forward propagation module. You will start by implementing some basic functions that you will use later when implementing the model. You will complete three functions in this order:
- LINEAR
- LINEAR -> ACTIVATION where ACTIVATION will be either ReLU or Sigmoid.
- [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID (whole model)
The linear forward module (vectorized over all the examples) computes the following equations:
Exercise: Build the linear part of forward propagation.
Reminder:
The mathematical representation of this unit is Z[l]=W[l]A[l−1]+b[l] . You may also find np.dot() useful. If your dimensions don’t match, printing W.shape may help.
定义前向线性函数:
def linear_forward(A,W,b):
Z=np.dot(W,A)+b
assert(Z.shape==(W.shape[0],A.shape[1]))
cache=(A,W,b)
return Z,cache测试:
A, W, b = linear_forward_test_case()
Z, linear_cache = linear_forward(A, W, b)
print("Z = " + str(Z))结果:
Z = [[ 3.26295337 -1.23429987]]4.2 - Linear-Activation Forward
前向线性激活函数,sigmoid和Relu。
In this notebook, you will use two activation functions:
- Sigmoid: σ(Z)=σ(WA+b)=11+e−(WA+b) . We have provided you with the sigmoid function. This function returns two items: the activation value “a” and a “cache” that contains “Z” (it’s what we will feed in to the corresponding backward function). To use it you could just call:
A, activation_cache = sigmoid(Z)- ReLU: The mathematical formula for
ReLuis A=RELU(Z)=max(0,Z). We have provided you with the relu function. This function returns two items: the activation value “A” and a “cache” that contains “Z” (it’s what we will feed in to the corresponding backward function). To use it you could just call:
A, activation_cache = relu(Z)For more convenience, you are going to group two functions (Linear and Activation) into one function (LINEAR->ACTIVATION). Hence, you will implement a function that does the LINEAR forward step followed by an ACTIVATION forward step.
Exercise: Implement the forward propagation of the LINEAR->ACTIVATION layer. Mathematical relation is:
A[l]=g(Z[l])=g(W[l]A[l−1]+b[l]) where the activation “g” can be sigmoid() or relu(). Use linear_forward() and the correct activation function.
def linear_activation_forward(A_prev,W,b,activation):
if activation == 'sigmoid':
Z,linear_cache=linear_forward(A_prev,W,b)
A, activation_cache=sigmoid(Z)
if activation == 'relu':
Z,linear_cache=linear_forward(A_prev,W,b)
A, activation_cache=relu(Z)
assert (A.shape == (W.shape[0], A_prev.shape[1]))
cache = (linear_cache, activation_cache)#activation为Z缓存
return A, cache测试:
A_prev, W, b = linear_activation_forward_test_case()
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "sigmoid")
print("With sigmoid: A = " + str(A))
A, linear_activation_cache = linear_activation_forward(A_prev, W, b, activation = "relu")
print("With ReLU: A = " + str(A))结果:
With sigmoid: A = [[ 0.96890023 0.11013289]]
With ReLU: A = [[ 3.43896131 0. ]]4.3 L-Layer Model
对于L层模型,前L-1层使用relu激活函数,最后一层用sigmoid函数
For even more convenience when implementing the L-layer Neural Net, you will need a function that replicates the previous one (linear_activation_forward with RELU) L−1 times, then follows that with one linear_activation_forward with SIGMOID.
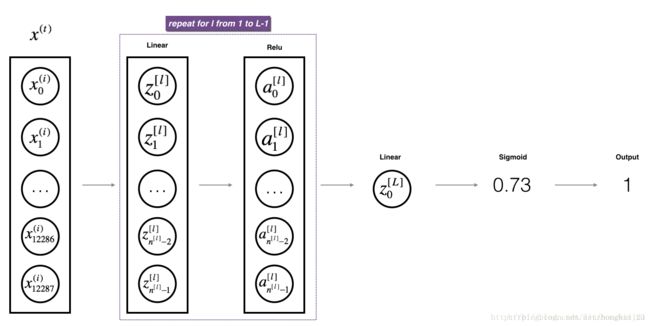
Figure 2 : [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID model
Exercise: Implement the forward propagation of the above model.
Tips:
- Use the functions you had previously written
- Use a for loop to replicate [LINEAR->RELU] (L-1) times
- Don’t forget to keep track of the caches in the “caches” list. To add a new value c to a list, you can use list.append(c).
L层神经网络前向传播模型函数,返回最终A和缓存各层的A_prev,W,b,Z
def L_model_forward(X,parameters):
caches=[]
A=X
L=len(parameters)//2
for l in range(1,L):#1~L-1层relu激活
A_prev=A
A,cache=linear_activation_forward(A_prev,parameters['W'+str(l)],parameters['b'+str(l)],'relu')
caches.append(cache)#cache A_prev W b Z
AL, cache = linear_activation_forward(A, parameters["W" + str(L)], parameters["b" + str(L)], "sigmoid")#L层sigmoid激活
caches.append(cache)
assert(AL.shape == (1,X.shape[1]))
return AL,caches测试:
X, parameters = L_model_forward_test_case()
AL, caches = L_model_forward(X, parameters)
print("AL = " + str(AL))
print("Length of caches list = " + str(len(caches))) 结果:
AL = [[ 0.17007265 0.2524272 ]]
Length of caches list = 25 - Cost function
计算损失函数
Now you will implement forward and backward propagation. You need to compute the cost, because you want to check if your model is actually learning.
Exercise: Compute the cross-entropy cost J, using the following formula:
def compute_cost(AL, Y):
m=Y.shape[1]
for i in range(m):
cost=-1/m*np.sum(np.multiply(Y,np.log(AL))+np.multiply((1-Y),np.log(1-AL)))
cost = np.squeeze(cost) # To make sure your cost's shape is what we expect (e.g. this turns [[17]] into 17).
assert(cost.shape == ())
return cost测试:
Y, AL = compute_cost_test_case()
print("cost = " + str(compute_cost(AL, Y)))结果:
cost = 0.4149315996156 - Backward propagation module
Just like with forward propagation, you will implement helper functions for backpropagation. Remember that back propagation is used to calculate the gradient of the loss function with respect to the parameters.
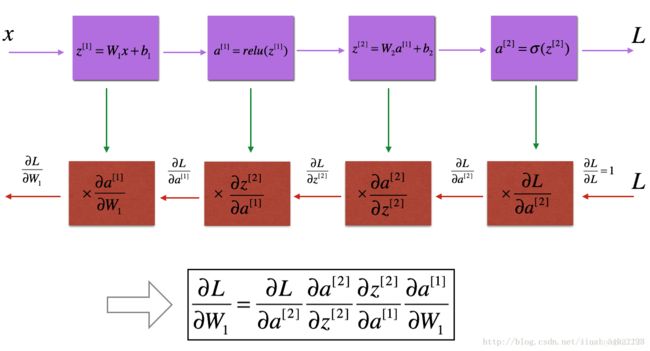
The purple blocks represent the forward propagation, and the red blocks represent the backward propagation.
In order to calculate the gradient dW[1]=∂L∂W[1] , you use the previous chain rule and you do dW[1]=dz[1]×∂z[1]∂W[1] . During the backpropagation, at each step you multiply your current gradient by the gradient corresponding to the specific layer to get the gradient you wanted. Equivalently, in order to calculate the gradient db[1]=∂L∂b[1] , you use the previous chain rule and you do db[1]=dz[1]×∂z[1]∂b[1] . This is why we talk about backpropagation. !–>
Now, similar to forward propagation, you are going to build the backward propagation in three steps:
- LINEAR backward
- LINEAR -> ACTIVATION backward where ACTIVATION computes the derivative of either the ReLU or sigmoid activation
- [LINEAR -> RELU] × (L-1) -> LINEAR -> SIGMOID backward (whole model)
6.1 - Linear backward
For layer l, the linear part is: Z[l]=W[l]A[l−1]+b[l] (followed by an activation).
Suppose you have already calculated the derivative dZ[l]=∂L∂Z[l] . You want to get ( (dW[l],db[l]dA[l−1]) ).
The three outputs ( (dW[l],db[l],dA[l]) ) are computed using the input dZ[l] .Here are the formulas you need:
dW[l]=∂L∂W[l]=1mdZ[l]A[l−1]T(8)
db[l]=∂L∂b[l]=1m∑mi=1dZ[l](i)(9)
dA[l−1]=∂L∂A[l−1]=W[l]TdZ[l](10)
Exercise: Use the 3 formulas above to implement linear_backward().
**实现一步线性的反向传播,使用对应层前向传播的缓存A_prev,W,b**
def linear_backward(dZ,cache):
A_prev, W, b = cache
m = A_prev.shape[1]
dW=1/m*np.dot(dZ,A_prev.T)
db=1/m*np.sum(dZ,axis=1,keepdims=True)
dA_prev=np.dot(W.T,dZ)
assert (dA_prev.shape == A_prev.shape)
assert (dW.shape == W.shape)
assert (db.shape == b.shape)
return dA_prev,dW,db测试:
dZ, linear_cache = linear_backward_test_case()
dA_prev, dW, db = linear_backward(dZ, linear_cache)
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))结果:
dA_prev = [[ 0.51822968 -0.19517421]
[-0.40506361 0.15255393]
[ 2.37496825 -0.89445391]]
dW = [[-0.10076895 1.40685096 1.64992505]]
db = [[ 0.50629448]]6.2 - Linear-Activation backward
Next, you will create a function that merges the two helper functions: linear_backward and the backward step for the activation linear_activation_backward.
To help you implement linear_activation_backward, we provided two backward functions:
- sigmoid_backward: Implements the backward propagation for SIGMOID unit. You can call it as follows:
dZ = sigmoid_backward(dA, activation_cache)- relu_backward: Implements the backward propagation for RELU unit. You can call it as follows:
dZ = relu_backward(dA, activation_cache)If g(.) is the activation function,
sigmoid_backward and relu_backward compute
Exercise: Implement the backpropagation for the LINEAR->ACTIVATION layer.
def linear_activation_backward(dA,cache,activation):
linear_cache,activation_cache=cache
if activation=='relu':
dZ=relu_backward(dA,activation_cache)#需要参数dA,Z
dA_prev,dW,db=linear_backward(dZ,linear_cache)#需要参数dZ,A_prev,W,b
if activation=='sigmoid':
dZ=sigmoid_backward(dA,activation_cache)#需要参数dA,Z
dA_prev,dW,db=linear_backward(dZ,linear_cache)#需要参数dZ,A_prev,W,b
return dA_prev, dW, db测试:
AL, linear_activation_cache = linear_activation_backward_test_case()
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "sigmoid")
print ("sigmoid:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db) + "\n")
dA_prev, dW, db = linear_activation_backward(AL, linear_activation_cache, activation = "relu")
print ("relu:")
print ("dA_prev = "+ str(dA_prev))
print ("dW = " + str(dW))
print ("db = " + str(db))结果:
sigmoid:
dA_prev = [[ 0.11017994 0.01105339]
[ 0.09466817 0.00949723]
[-0.05743092 -0.00576154]]
dW = [[ 0.10266786 0.09778551 -0.01968084]]
db = [[-0.05729622]]
relu:
dA_prev = [[ 0.44090989 0. ]
[ 0.37883606 0. ]
[-0.2298228 0. ]]
dW = [[ 0.44513824 0.37371418 -0.10478989]]
db = [[-0.20837892]]6.3 - L-Model Backward
Now you will implement the backward function for the whole network. Recall that when you implemented the L_model_forward function, at each iteration, you stored a cache which contains (X,W,b, and z). In the back propagation module, you will use those variables to compute the gradients. Therefore, in the L_model_backward function, you will iterate through all the hidden layers backward, starting from layer L. On each step, you will use the cached values for layer l to backpropagate through layer l.
To backpropagate through this network, we know that the output is,
A[L]=σ(Z[L])
4. Your code thus needs to compute dAL=∂L∂A[L] .
To do so, use this formula (derived using calculus which you don’t need in-depth knowledge of):
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))# derivative of cost with respect to *AL*You can then use this post-activation gradient dAL to keep going backward. you can now feed in dAL into the LINEAR->SIGMOID backward function you implemented (which will use the cached values stored by the L_model_forward function). After that, you will have to use a for loop to iterate through all the other layers using the LINEAR->RELU backward function. You should store each dA, dW, and db in the grads dictionary. To do so, use this formula :
grads["dW"+str(l)]=dW[l](15)
For example, for l=3 this would store dW[l]ingrads["dW3"] .
Exercise: Implement backpropagation for the [LINEAR->RELU] × (L-1) -> LINEAR -> SIGMOID model.
def L_model_backward(AL,Y,caches):
grads={}
#linear_cache,activation=cache
L=len(caches)
Y=Y.reshape(AL.shape)
dAL=-(np.divide(Y,AL)-np.divide(1-Y,1-AL))
grads["dA" + str(L)], grads["dW" + str(L)], grads["db" + str(L)]=linear_activation_backward(dAL,caches[L-1],'sigmoid')
for l in reversed(range(L - 1)):
grads["dA" + str(l+1)], grads["dW" + str(l+1)], grads["db" + str(l+1)]=linear_activation_backward(grads["dA" + str(l+2)],caches[l],'relu')
return grads测试:
AL, Y_assess, caches = L_model_backward_test_case()
grads = L_model_backward(AL, Y_assess, caches)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dA1 = "+ str(grads["dA1"]))结果:
dW1 = [[ 0.41010002 0.07807203 0.13798444 0.10502167]
[ 0. 0. 0. 0. ]
[ 0.05283652 0.01005865 0.01777766 0.0135308 ]]
db1 = [[-0.22007063]
[ 0. ]
[-0.02835349]]
dA1 = [[ 0. 0.52257901]
[ 0. -0.3269206 ]
[ 0. -0.32070404]
[ 0. -0.74079187]]6.4 - Update Parameters
In this section you will update the parameters of the model, using gradient descent:
where α is the learning rate. After computing the updated parameters, store them in the parameters dictionary.
Exercise: Implement update_parameters() to update your parameters using gradient descent.
Instructions:
Update parameters using gradient descent on every W[l] and b[l] for l=1,2,…,L.
def update_parameters(parameters, grads, learning_rate):
L = len(parameters) // 2 # number of layers in the neural network
for l in range(L):
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate * grads["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate * grads["db" + str(l+1)]
return parameters测试:
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads, 0.1)
print ("W1 = "+ str(parameters["W1"]))
print ("b1 = "+ str(parameters["b1"]))
print ("W2 = "+ str(parameters["W2"]))
print ("b2 = "+ str(parameters["b2"]))结果:
W1 = [[-0.59562069 -0.09991781 -2.14584584 1.82662008]
[-1.76569676 -0.80627147 0.51115557 -1.18258802]
[-1.0535704 -0.86128581 0.68284052 2.20374577]]
b1 = [[-0.04659241]
[-1.28888275]
[ 0.53405496]]
W2 = [[-0.55569196 0.0354055 1.32964895]]
b2 = [[-0.84610769]]7 - Conclusion
Congrats on implementing all the functions required for building a deep neural network!
We know it was a long assignment but going forward it will only get better. The next part of the assignment is easier.
In the next assignment you will put all these together to build two models:
- A two-layer neural network
- An L-layer neural network
You will in fact use these models to classify cat vs non-cat images!