拉格朗日插值&&最小二乘法原理简述

最小二乘法简述及推导，转自：点击打开链接

经常做物理实验的同学应该会有这样的体会，我们经常需要将实验收集得来的数据标注在一个坐标平面之上，形成一系列离散的点，然后用一条平滑的曲线近似地将这些点连在一起，借此推测实验变量之间的函数关系，对实验结果进行理论分析。这种方法能够帮助实验人员用数学语言描述物理现象，广受欢迎，专业上的说法，称为“曲线拟合”。

“曲线拟合”的结果当然可以五花八门，比如碰到下面这个图象

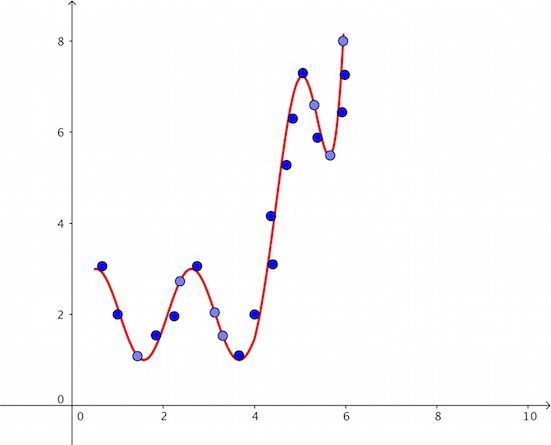让你说出实验变量x与y之间的函数关系，十有八九你会一脸懵圈：这是个什么鬼？你在玩贪吃蛇吗？

 

但若是实验数据呈现出下面这个形态的分布，你应该就会爽快地不假思索地答出：这是一条直线！

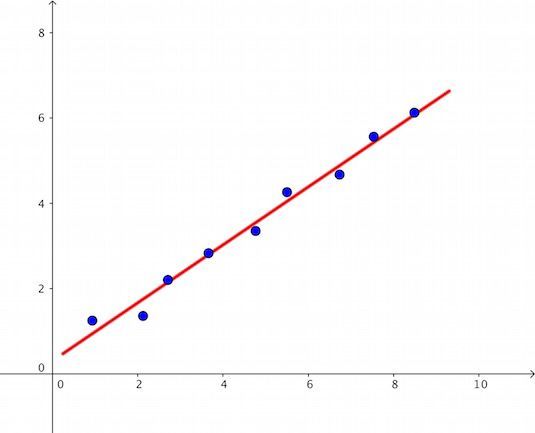没错，考虑到可能的实验误差，认定上述变量之间的函数关系满足一个直线方程是一件非常靠谱的事情，问题是如何把这条直线给找出来？

 

对数学而言，“平面直线千千万，这条不好你再换”之类的“随手画”是丝毫没有说服力的，你必须建立恰当的模型，并且明确相应的判断标准。

模型我们已经有了——直线：，判断标准也很容易达成共识：实验采集到的数据与真实值之间的差距尽可能的小。接下来的任务，就是要将直线拟合的过程转化为一个数学问题的求解。

在数学上，“实验采集到的数据与真实值之间的差距尽可能的小”是通过求解下面这个极值问题来实现的。假设实验采集到组数据，我们要求方程系数的选取使得函数

 

的取值尽可能的小（最好是0）。

 

如何做到呢？看起来有些麻烦，老师没教过啊……要是变元的个数只有一个就好了，因为我们知道一元函数若在点处可微，那么它在处取极值的必要条件是，只要我们求出了方程的解，就知道了潜在的极值点。这个结论被称为微积分学中的费马定理，从几何上很好解释，你在坐标平面中随便画一条曲线，如果它在某一点处存在切线并且在此点取到极值，那么这条切线必定是平的（斜率为0）。

其实多元函数也是如此。

让我们短暂进入多元微积分的世界，一个多元函数如果在某一点可微并且取到极值，那么它在此点每一个方向上的导数都必须是0。特别的，此多元函数对各个变元的偏导数为0。比如我们关心的函数

 

有两个变元，它取极值的必要条件就是

 

。

这是一个关于的二元一次线性方程组，可以证明，你能解出唯一的一组并且它恰好使函数达到极小。

这个方法就是数学中大名鼎鼎的“最小二乘法”，因为求极值的函数由误差的平方项构造而得名，法国数学家勒让德（就是独立解决费马大定理情形的那位）最早发明了它。

如果你愿意深入研究一下，一定会对构造函数时使用误差的平方项感到疑惑，虽然直接累加误差的方式肯定不靠谱（较大的正负误差可能相互抵消），但累加误差的绝对值应该可以吧，为什么不对求极小确定的值呢？

最现实的原因就是，绝对值函数不是一般的初等函数，极值原理没法搞啊……

我并不是在跟大家开玩笑，利用误差绝对值进行数据整理的“最小一乘法”甚至早于“最小二乘法”而出现，但是苦于没有优良的算法而被埋没，直到上个世纪中叶才因为计算机的发明和统计学的迅猛发展重新闪光。

除了算法方面有优势外，“最小二乘法”的计算结果也更加符合人们长久以来形成的认知。比如我们对某个未知量多次测量得到一组数据（按照从小到大的顺序排列），采用“最小二乘法”对其真实值进行估算，使函数

 

达到极小的值为，即数据的算术平均值。若采用“最小一乘法” 对真实值进行估算，使函数

 

 

达到极小的值分两种情况：当为偶数时，它是区间中的任何一个数；当为奇数时，它是数据的中位数（一个点A在数轴上到另外两点B、C距离之和的最小值必当点A位于B、C之间时取到）。因为我们在很长时间里已经习惯重复测量取平均的做法，算术平均就比中位数“更加让人信赖”，“最小二乘法”也就比“最小一乘法”更受欢迎了。

 

这种说法听起来很有道理，事实上却没能堵住数学家们的质疑，它只说明了某些情况下采用“最小二乘法”的优势，并不能说明“最小二乘法”就是“曲线拟合”所能采取的最好方法呀！

对此，高斯同志给出了一个回答：如果我们把等待拟合的数据看成是一次统计实验的结果（就像不断抛硬币看正反面那样），那么其误差应该近似地满足正态分布。已经接触过概率论和统计学的朋友不妨拿出纸笔算上一算，利用正态分布的概率密度函数进行极大似然估计，结果不偏不倚，正好就是“最小二乘”。

因为这一绝妙的解释，许多人都把“最小二乘法”的功劳记在了高斯的帐下。这位数学王子也没跟老前辈客气，主动声称对“最小二乘法”的出现负责，为此还专门跟比自己大了两轮的勒让德叔叔吵了一架，热闹程度不亚于牛顿和莱布尼兹对微积分发明权的争夺。这段分歧现在也成为了数学史上一桩无解的公案，不过人们也乐于让两位大家共同分享这份“发明”的荣耀。需要说明的是，高斯的理论也并非完美无暇，误差满足正态分布的说法是一个无条件的预设，并不自然，应用棣莫弗和拉普拉斯的中心极限定理才能得到一个比较圆满的解释：若把误差理解为大量的独立随机变量之和，那么误差的理论分布应该是正态分布。当然，假若失去了这一前提，“最小二乘法”就不再是最为恰当的拟合方法了。

这个版本就跟高数书上类似了~转自：点击打开链接

 

最小二乘是每个上过大学的同学都接触过的概念与知识点(当然可能纯文科的同学没接触过，但是一般纯文科的同学也不会看这篇文章好像)。最小二乘理论其实很简单，用途也很广泛。但是每次说到最小二乘，总感觉差了点什么似的，好像对于最小二乘的前世今生没有一个特别详细与系统的了解。so，本博主趁着周末的时间，赶紧给详细整理整理，力争把最小二乘是个什么鬼做一个特别详细的说明，争取让学英语学中文学历史学画画唱歌的同学都能看明白。

1.最小二乘的背景

这种东东的来源，比较容易找到而且比较靠谱的途径自然是wiki百科了，以下部分的内容来自wiki百科： 
1801年，意大利天文学家朱赛普·皮亚齐发现了第一颗小行星谷神星。经过40天的跟踪观测后，由于谷神星运行至太阳背后，使得皮亚齐失去了谷神星的位置。随后全世界的科学家利用皮亚齐的观测数据开始寻找谷神星，但是根据大多数人计算的结果来寻找谷神星都没有结果。时年24岁的高斯也计算了谷神星的轨道。奥地利天文学家海因里希·奥伯斯根据高斯计算出来的轨道重新发现了谷神星。 
高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中，而法国科学家勒让德于1806年独立发现“最小二乘法”，但因不为世人所知而默默无闻。两人曾为谁最早创立最小二乘法原理发生争执。1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明，见高斯-马尔可夫定理。

2.举个最简单的例子理解最小二乘

现在大家都越来越重视自己的身体健康。现代人最常见的亚健康问题就是肥胖，本博主身体棒棒哒，唯一困扰本博主的健康问题就是超重。（好吧，承认自己是个死胖子就完了） 
假设身高是变量X，体重是变量Y，我们都知道身高与体重有比较直接的关系。生活经验告诉我们：一般身高比较高的人，体重也会比较大。但是这只是我们直观的感受，只是很粗略的定性的分析。在数学世界里，我们大部分时候需要进行严格的定量计算：能不能根据一个人的身高，通过一个式子就能计算出他或者她的标准体重？ 
接下来，我们肯定会找一堆人进行采用（请允许我把各位当成一个样本）。采样的数据，自然就是各位的身高与体重。（为了方便计算与说明，请允许我只对男生采样）经过采样以后，我们肯定会得到一堆数据(x1,y1),(x2,y2),⋯,(xn,yn)，其中x是身高，y是体重。 
得到这堆数据以后，接下来肯定是要处理这堆数据了。生活常识告诉我们：身高与体重是一个近似的线性关系，用最简单的数学语言来描述就是y=β0+β1x。于是，接下来的任务就变成了：怎么根据我们现在得到的采样数据，求出这个β0与β1呢？这个时候，就轮到最小二乘法发飙显示威力了。

3.最小二乘的cost function

在讲最小二乘的详情之前，首先明确两点：1.我们假设在测量系统中不存在有系统误差，只存在有纯偶然误差。比如体重计或者身高计本身有问题，测量出来的数据都偏大或者都偏小，这种误差是绝对不存在的。（或者说这不能叫误差，这叫错误）2.误差是符合正态分布的，因此最后误差的均值为0（这一点很重要) 
明确了上面两点以后，重点来了：为了计算β0,β1的值，我们采取如下规则：β0,β1应该使计算出来的函数曲线与观察值的差的平方和最小。用数学公式描述就是： 

Q=min∑in(yie−yi)2

其中，yie表示根据y=β0+β1x估算出来的值，yi是观察得到的真实值。

 

可能有很多同学就会不服了，凭什么要用差的平方和最小勒？用差的绝对值不行么？不要骗我们好不好？ 
本博主不敢骗大家，为了让大家相信，特意找了一种本博主认为比较靠谱的解释： 
我们假设直线对于坐标 Xi 给出的预测 f(Xi) 是最靠谱的预测，所有纵坐标偏离 f(Xi) 的那些数据点都含有噪音，是噪音使得它们偏离了完美的一条直线，一个合理的假设就是偏离路线越远的概率越小，具体小多少，可以用一个正态分布曲线来模拟，这个分布曲线以直线对 Xi 给出的预测 f(Xi) 为中心，实际纵坐标为 Yi 的点 (Xi, Yi) 发生的概率就正比于 EXP[-(ΔYi)^2]。（EXP(..) 代表以常数 e 为底的多少次方）。 
所以我们在前面的两点里提到，假设误差的分布要为一个正态分布，原因就在这里了。 
另外说一点我自己的理解：从数学处理的角度来说，绝对值的数学处理过程，比平方和的处理要复杂很多。搞过机器学习的同学都知道，L1正则就是绝对值的方式，而L2正则是平方和的形式。L1能产生稀疏的特征，这对大规模的机器学习灰常灰常重要。但是L1的求解过程，实在是太过蛋疼。所以即使L1能产生稀疏特征，不到万不得已，我们也还是宁可用L2正则，因为L2正则计算起来方便得多。。。

4.最小二乘法的求解

明确了前面的cost function以后，后面的优化求解过程反倒变得so easy了。 
样本的回归模型很容易得出： 

Q=∑in(yi−β0−β1x)2

现在需要确定β0、β1，使cost function最小。学过高数的同志们都清楚，求导就OK。对于这种形式的函数求导，so easy，so happy…

 

 

∂Q∂β0=2∑in(yi−β0−β1xi)(−1)=0∂Q∂β1=2∑in(yi−β0−β1xi)(−xi)=0

 

将这两个方程稍微整理一下，使用克莱姆法则，很容易求解得出： 

β0=∑x2i∑yi−∑xi∑xiyin∑x2i−(∑xi)2β1=n∑xiyi−∑xi∑yin∑x2i−(∑xi)2

 

因为求和符号比较多，省略了上标与下标。 
根据这个公式，就可以求解出相应的参数。 
对应上面的身高体重关系的例子，我们只需要将采样得到的数据，一一代入即可求解。

5.矩阵表达形式

如果我们推广到更一般的情况，假如有更多的模型变量x1,x2,⋯,xm（注意：x1是指 一个样本，x1是指样本里的一个模型相关的变量)，可以用线性函数表示如下： 

y(x1,⋯,xm;β0,⋯,βm)=β0+β1x1+⋯+βmxm

对于n个样本来说，可以用如下线性方程组表示： 

 

β0+β1x11+⋯+βjxj1+⋯+βmxm1=y1β0+β1x12+⋯+βjxj2+⋯+βmxm2=y2⋯β0+β1x1i+⋯+βjxji+⋯+βmxmi=yi⋯β0+β1x1n+⋯+βjxjn+⋯+βmxmn=yn

 

 

如果将样本矩阵xhi记为矩阵A,将参数矩阵记为向量β，真实值记为向量Y，上述线性方程组可以表示为：

 

⎡⎣⎢⎢⎢⎢⎢11⋯1x(1)1x(2)1⋯x(m)1⋯⋯⋯⋯x(1)nx(2)n⋯x(m)n⎤⎦⎥⎥⎥⎥⎥⋅⎡⎣⎢⎢⎢⎢β0β1⋯βm⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢y0y1⋯yn⎤⎦⎥⎥⎥⎥

即Aβ=Y 
对于最小二乘来说，最终的矩阵表达形式可以表示为： 

 

min||Aβ−Y||2

最后的最优解为： 

 

 

β=(ATA)−1ATY

 

 

6.注意事项

经典的最小二乘法使用起来够简单粗暴，计算过程也不复杂。但是一个致命的问题就是其对噪声的容忍度很低。试想一下，如果前面我们得到的总采样数据为100个，但是里面有几个大胖子，这几个大胖子就相当于不是普通人的身高-体重系数，他们就是噪声了。如果不采取一些手段对这几个噪声样本进行处理，最后计算出来的身高-体重系数肯定会比正常值要偏大。 
对于噪声的处理，比如有加权最小二乘等方法，后续有时间跟大家再讲讲。

拉格朗日插值法，图文并茂，讲的很清楚~转自：点击打开链接