结合matlab代码案例解释ICA独立成分分析原理
目录
-
- 介绍
-
- 什么是ICA?
- 对数据进行白化
- ICA算法
- ICA特性
本分享为脑机学习者Rose整理发表于公众号:脑机接口社区(微信号:Brain_Computer).QQ交流群:941473018
![]()
关于ICA,可以查看Rose小哥之前分享的《ICA独立成分分析去除EEG伪影》以及Scott等大神关于ICA的原理与应用的文献汇总《Scott等大神的33篇ICA独立成分分析论文汇总》。
介绍
独立分量分析是一种将多个传感器中的独立源线性混合分离的信号处理方法。例如,当在头皮上记录脑电图(EEG)时,ICA可以分离出嵌入在数据中的伪像(因为它们通常彼此独立)。
什么是ICA?
ICA是一种分离线性混合源的技术。例如,我们可以尝试混合然后分开两个源。
下面,我们定义两个独立源A(顶部)和B(底部)的时间过程(matlab代码在后文中有提供)

然后,我们将这两个源线性混合。顶部曲线等于A减去B的两倍,而底部线性组合为1.73 * A + 3.41 * B。

然后,将这两个信号输入ICA算法(在本例中为fastICA),该算法能够发现A和B的原始激活。
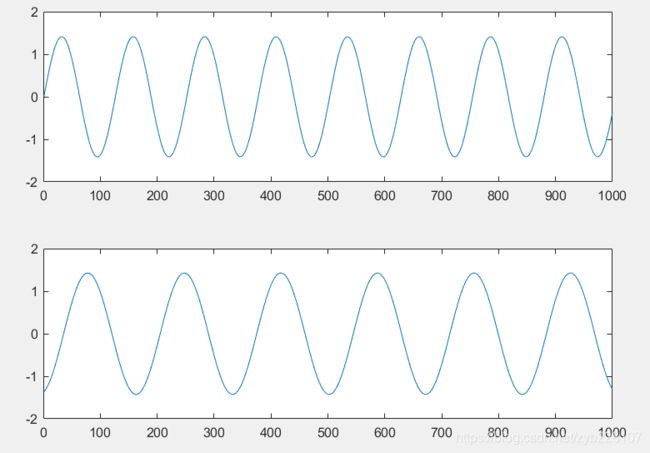
请注意,该算法无法恢复源活动的确切振幅(稍后可以看到原因)。建议尝试使用不同程度的噪音进行测试,看看它是相当稳健。值得注意的是,从理论上讲,ICA只能提取线性组合的源。
对数据进行白化
不过在使用ICA算法之前,需要说明一下大多数ICA算法在实际应用ICA之前需要执行的预处理。
许多ICA算法的第一步是白化数据。这意味着我们删除了数据中的所有相关性,即不同的通道(矩阵Q)必须保证不相关。
为什么这样做呢?一个几何解释是,它恢复数据的初始“形状”,然后ICA必须只旋转结果矩阵(见下文)。
下面,再次将两个随机的源A和B混合。在下图中,A的值是数据点的横坐标,B的值是它们的纵坐标。(见代码 ica_test2.m)

取A和B的两个线性混合物,并绘制这两个新变量

然后,如果我们把这两种线性混合物白化,就得到下面的图

两个轴上的方差现在是相等的,数据在两个轴上的投影的相关性是0(意味着协方差矩阵是对角的,所有对角线上的元素都是相等的)。然后应用ICA仅意味着将这个表示“旋转”回原始的A和B轴空间。
白化过程只是混合数据坐标的线性变化。一旦在这个“白化”的坐标系中找到ICA解决方案,我们就可以轻松地将ICA解决方案重新投影到原始的坐标系中。
ICA算法
直观地,您可以想象ICA将白化的矩阵旋转回原始(A,B)空间(上面的第一个散点图)。它通过最小化投影在两个轴(固定点ICA)上的数据的高斯性来实现旋转。例如,在上面的例子中,
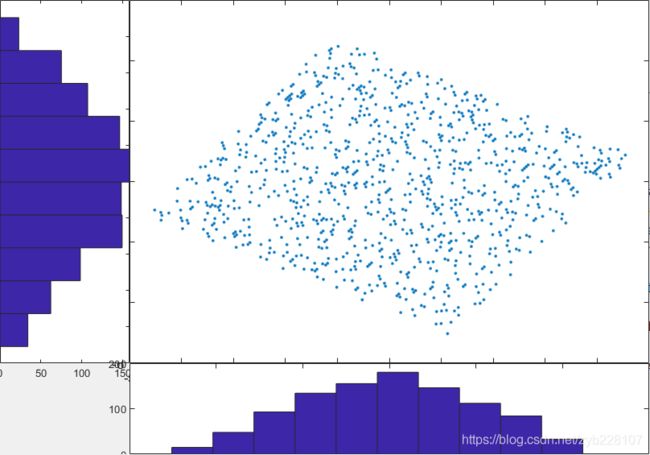
在两个轴上的投影是类似于高斯的(即看起来像一个钟形曲线)。相比之下,投影在原A、B空间中远离高斯分布。

通过旋转轴并在第一个散点图最小化投影Gaussianity,ICA可以恢复统计上独立的原始源(这个属性来自于中心极限定理,该定理指出在满足某种条件时,独立随机变量的和趋于高斯分布,从而使得独立随机变量的和比任何一个原始随机变量都更接近于高斯分布)。在Matlab中,函数峰度(在EEGLAB工具箱中的kurt();在Matlab统计工具箱中的kurtosis())指示了分布的高斯性(但是定点ICA算法使用了一个稍微不同的度量,称为负熵)。
EEGLAB工具箱中的Infomax ICA (Infomax ICA)并没有那么直观,它涉及到最小化投影在两个轴上的数据的相互信息。当然,即使ICA算法在数值上有所不同,但在理论上都是等价的。
ICA处理n维数据
上面只处理了二维空间。但是ICA可以处理任意数量的维。让我们以128个脑电图电极为例。在每个时间点记录在所有电极上的信号构成一个128维空间中的数据点。在白化数据之后,ICA将“旋转128轴”,以最小化投影在所有轴上的高斯性(注意,与PCA不同,轴不必保持正交)。
我们所称的ICA分量是一个矩阵,它允许将初始空间中的数据投影到ICA找到的轴上。权重矩阵是原始空间的完整变换。
下面使用一个例子来说明:
S = W X S=WX S=WX
X是原始空间中的数据,S是源活动。
对于脑电图数据来说:

对于fMRI数据来说:

在脑电图中:伪影时间过程或大脑中一个紧凑域的时间过程

在fMRI中:伪影地形或统计上最大独立激活模式的地形图
W是从S空间到X空间的权重矩阵。
现在,W的行是向量,通过它,可以计算一个独立成分的活动。为了计算,公式S = W X中的分量活度,权重矩阵W定义为

例如,要计算第二个源或第二个独立分量的活动(以矩阵乘法格式),您可以简单地用行向量乘以矩阵X。

现在有了第二个分量的活动,但是活动是没有单位的。如果听说过逆建模,那么在偶极子定位软件中与EEG/ERP源的类比是最容易理解的。每个偶极子都有一个活动(线性地投射到所有电极上)。除非将其投射到电极上,否则大脑源的活动(偶极子)是无单位的。
现在我们将看到如何将一个分量重新投影到电极空间。
W − 1 W^{-1} W−1是从源空间 S S S到数据空间 X X X的逆矩阵。
X = W − 1 S X=W^{-1}S X=W−1S
在Matlab中,只需要输入inv(W)就可以得到一个矩阵的逆。

如果S是一个行向量(例如上面计算的分量2的活动),我们将它乘以上面逆矩阵中的列向量.

我们将得到分量2的投影活动(分量2的逆权值(列向量;左下)乘以组件2的活动(行向量;右上)引出分量投影(矩阵;右下角)。

现在,如果想要从数据中删除分量2(例如,如果分量2被证明是伪迹),在可以简单地从原始数据X中减去上面的矩阵(XC2)。
注意,在上面计算的矩阵(XC2)中,所有列都是成比例的,这意味着头皮活动只是按比例缩放。
因此,我们表示W-1矩阵的列,即各成分的头皮形貌。
这个矩阵的每一列都是一个分量的地形,它随时间由该分量的活度缩放。每个分量的头皮形貌可用于估计该组件的等效偶极子位置(假设该分量不是伪迹)。
综上所述,当我们讨论独立分量时,我们通常会提到两个概念
矩阵的行是分量活动的时间过程
矩阵的列是分量的头皮投影
ICA特性
从前面的介绍可以看出ICA的几个特性:
- ICA只能分离线性混合的源。
- 由于ICA处理的是点云,因此改变点的绘制顺序(EEG中的时间点顺序)对算法的结果几乎没有影响。
- 改变通道顺序(例如在EEG中交换电极位置)也不会影响算法的结果。对于脑电信号来说,该算法对电极位置没有先验知识,ICA分量在大多数情况下可以被解析为一个等效偶极子,这证明了ICA能够分离出皮层同步化的致密区域。
- 由于独立分量分析通过最大化源的非高斯性来分离源,所以完美的高斯源是不能被分离的。
- 即使信息源不是独立的,独立分量分析也能找到一个最大独立空间。
请在关注公众号,在公众号后台留言"ICA code"获取包括FastICA、ica_test1.m、ica_test2.m等代码案例。
参考文献
Jung T-P, Makeig S, Humphries C , Lee TW, McKeown MJ, Iragui V, and Sejnowski TJ, “Removing Electroencephalographic Artifacts by Blind Source Separation,” Psychophysiology, 37:163-78, 2000 (.pdf, 1.3Mb).
Jung T-P, Makeig S, Westerfield W, Townsend J, Courchesne E, and Sejnowski TJ, "Removal of eye activity artifacts from visual event-related potentials in normal and clinical subjects,"Clinical Neurophysiology 111:1745-58, 2000 (.pdf, 4.9Mb).
参考
结合matlab代码案例解释ICA独立成分分析原理
本文章由脑机学习者Rose笔记分享,QQ交流群:941473018
更多分享,请关注公众号
![]()