使用回溯法求解装载问题
回溯法解决装载问题(java实现)
-
问题描述:有n个集装箱要装上两艘载重量分别为C1和C2的轮船,其中集装箱i的重量为wi,且:∑ wi ≤ C1+C2。 求是否有一个合理的装载方案能将这 n 个集装箱装上这两艘轮船。
-
分析:假设wt 为装上第一艘轮船的集装箱的重量之和。此时,如果有
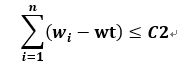
,则问题有解;否则问题无解。所以,该问题是在 wt ≤ C1的前提下,寻找 wt 最大值,使得C1 -wt 尽量小,等价于如何将第一艘轮船尽可能装满。而如何将第一艘轮船尽可能装满等价于选取全体集装箱的一个子集,使该子集中集装箱的重量之和最接近C1。所以该问题可以形式化描述为

设有3个集装箱要装上两艘重量分别为C1和C2的轮船,C1=C2=30,w={16,15,15}。问是否有一个合理的方案能将这3个集装箱装上两艘船?采用回溯法求解该问题。
1. 定义问题的解空间
对于有3个集装箱要装上轮船的装载问题,其解空间由长度为3的0-1向量即{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)}组成。
2. 建立解空间结构
装载问题的解空间结构是一棵完全二叉树。解空间树中每个结点都有左右两个分支,左分支用1标识,表示把第 i 个集装箱放上轮船,右分支用0标识,表示不把集装箱 i 放上轮船。解空间树的第i层到第 i+1层边上的标号给出了变量的值,从树根到叶的任意一条路径表示解空间中的一个元素。例如,从根结点A到叶结点 L 的路径对应于解空间中的元素(0,1,1)。装载问题的解空间树如图所示。
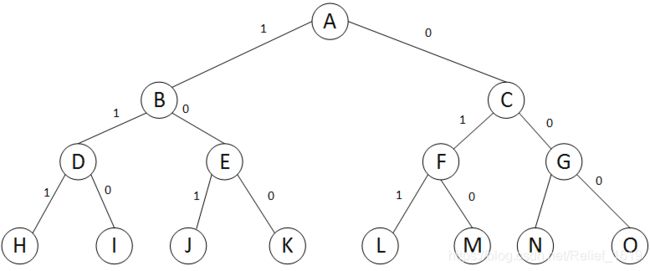
3. 采用回溯法以深度优先的方式搜索解空间树
初始时结点A是活结点并且是当前的可扩展结点,结点A有2个子结点,即B和C。左分支用1标识,表示把集装箱1放上第一艘轮船, 右分支用0标识,不把集装箱1放上轮船。 结点A是根结点,根结点在第一层,i从1开始调用回溯算法框架,即使用函数backtrack(1)开始搜索进程。注意,此时除集装箱1外,岸上剩余集装箱(集装箱2和集装箱3)的重量之和为30 (r=30)。
在搜索过程中,为了加快搜索的进程,避免无效搜索,在进入左子树之前,需设置约束函数在扩展结点处剪去不满足的约束条件的子树;在进入右子树之前,需设置限界函数在扩展结点处剪去不能得到最优解的子树。首先检测左子树处是否满足约束条件。
如图:
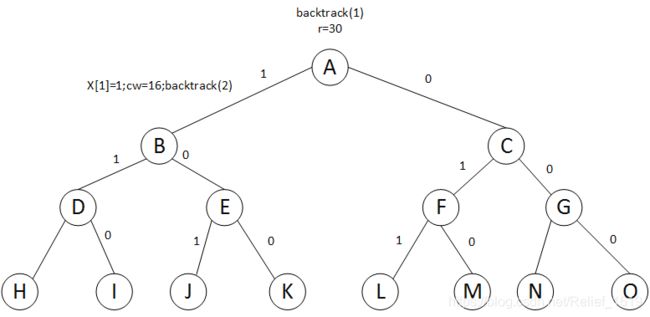
用cw表示当前已放上轮船的集装箱的重量和,w[1]为集装箱 1 的重量,C1是第一艘轮船的载重。因为cw+w[1]≤C1,结点B满足约束条件,可以将集装箱1放上轮船,x[1]=1,cw=16。结点B成为活结点并成为当前可扩展结点,递归函数backtrack(2)开始向结点B的下一层进行搜索。以此类推,直到找到整个问题的最优解。
代码实现
package backtrack;
public class Loading {
int number; //集装箱的数量
int[] w; //集装箱重量数组,记录每个集装箱的重量
int c1; // 第一艘轮船的载重量
int cw; //当前的载重量
int bestw; // 当前最优载重量
int r; //剩余集装箱重量
int[] x; //当前解
int[] bestx; //当前最优解
public void maxLoading(int n,int[] ww,int cc) {
//初始化数据成员
w=ww;
c1=cc;// 第一艘轮船的载重量
cw=0;//当前的载重量
bestw=0;// 当前最优载重量
number=n;
x=new int[n+1];
bestx=new int[n+1];
for(int i=1;i<=n;i++) {
r+=w[i]; //初始化r
}
//调用backtrack(i)函数计算最优载重量
backtrack(1);
//输出最佳装载方案
System.out.println("最优装载方案为:");
for(int k=1;k<=n;k++) {
System.out.print(bestx[k]+" ");
}
System.out.println();
//输出最优装载量
System.out.println("最优装载量为:"+bestw);
}
//回溯法实现求解最优装载问题
public void backtrack(int i){
//搜索第i层结点
if(i>number)
{
//到达叶节点
for(int j=1;j<=number;j++) {
bestx[j]=x[j];
}
bestw=cw;
return;
}
//搜索子树
r-=w[i];
if(cw+w[i]<=c1)
{
//搜索左子树
x[i]=1;
cw+=w[i];
backtrack(i+1);
cw-=w[i];
}
if(cw+r>bestw) {
// 搜索右子树
x[i]=0;
backtrack(i+1);
}
r+=w[i];
}
public static void main(String[] args) {
int n=3;//集装箱的数量
int c=30;//第一艘轮船的载重量
int[] weight= {
0,16,15,15};//集装箱重量数组
Loading l=new Loading();
l.maxLoading(n,weight,c);
}
}
当然,在最后我们还得检验一下,在轮船1达到最优载重量时,剩余的集装箱总重量是否超出轮船2的载重量,如果超出,那么该问题仍是无解的。
package backtrack;
public class Loading {
int number; //集装箱的数量
int[] w; //集装箱重量数组,记录每个集装箱的重量
int totalWeight;//集装箱总重量
int c1; // 第一艘轮船的载重量
int c2; // 第二艘轮船的载重量
int cweight2;// 第二艘轮船需要装载的重量
int cw; //当前的载重量
int bestw; // 当前最优载重量
int r; //剩余集装箱重量
int[] x; //当前解
int[] bestx; //当前最优解
public void maxLoading(int n,int[] ww,int c1,int c2) {
//初始化数据成员
w=ww;
this.c1=c1;// 第一艘轮船的载重量
this.c2=c2;// 第一艘轮船的载重量
cweight2=0;
cw=0;//当前的载重量
bestw=0;// 当前最优载重量
number=n;
x=new int[n+1];
bestx=new int[n+1];
for(int i=1;i<=n;i++) {
r+=w[i]; //初始化r
totalWeight+=w[i]; //初始化totalWeight
}
//调用backtrack(i)函数计算最优载重量
backtrack(1);
//计算第二艘轮船需要的装载量
cweight2=totalWeight-bestw;
//输出最佳装载方案
if(cweight2<= c2) {
//如果第二艘轮船需要的装载量小于其载重量,则两艘轮船可以装载所有物品
System.out.println("可以装载所有货物!");
System.out.println("第一艘轮船的最优装载方案为:");
for(int k=1;k<=n;k++) {
System.out.print(bestx[k]+" ");
}
System.out.println();
//输出最优装载量
System.out.println("第一艘轮船的最优装载量为:"+bestw);
System.out.println("第二艘轮船需要装载的重量为:"+cweight2);
}
else {
System.out.println("无法装载所有货物!");
}
}
//回溯法实现求解最优装载问题
public void backtrack(int i){
//搜索第i层结点
if(i>number)
{
//到达叶节点
for(int j=1;j<=number;j++) {
bestx[j]=x[j];
}
bestw=cw;
return;
}
//搜索子树
r-=w[i];
if(cw+w[i]<=c1)
{
//搜索左子树
x[i]=1;
cw+=w[i];
backtrack(i+1);
cw-=w[i];
}
if(cw+r>bestw) {
// 搜索右子树
x[i]=0;
backtrack(i+1);
}
r+=w[i];
}
public static void main(String[] args) {
int n=3;//集装箱的数量
int c1=30;//第一艘轮船的载重量
int c2=30;
int[] weight= {
0,16,15,15};//集装箱重量数组
Loading l=new Loading();
l.maxLoading(n,weight,c1,c2);
}
}