高斯投影

坐标转换–高斯投影

---

1. 什么是高斯投影

高斯投影是地球椭球面和平面之间的一种正行投影。属于等角横切椭圆柱投影。可以想象地球为一个椭球，将赤道面作为水平面，用一个同样水平放置的圆柱将该椭球套在内部，然后把椭球投影在圆柱面上，最后把圆柱面展开，就得到了高斯投影的结果。在我国高斯投影分为3度带和6度带，大于1:1万地形图采用3度带，1:2.5万至1:50万的地形图采用6度带投影，每一个投影带都有一个中央经线，在投影过程中，中央经线就是与圆柱面相切的线。根据以上特点，我们可以发现，高斯投影后中央经线长度保持不变，赤道线为直线，但是长度有变形，越远离中央经线，变形越大，其余经线凹向中央经线，其余纬线凸向赤道线。

2. 计算公式

正算公式

其中，ρ”在使用弧度角时值为1；X为子午线弧长；t为B的正切值；l”为经度差；η计算公式：

η = e2*cosB

e2为椭球第二偏心率，X（子午线弧长）计算公式如下：

 m0 = a * (1 - e1*e1);
 m2 = 3 * (e1 * e1 * m0) / 2.0;
 m4 = 5 * (e1 * e1 * m2) / 4.0;
 m6 = 7 * (e1 * e1 * m4) / 6.0;
 m8 = 9 * (e1 * e1 * m6) / 8.0;

 a0 = m0 + m2/2.0 + 3*m4/8.0 + 5*m6/16.0 + 35*m8/128.0;
 a2 = m2/2.0 + m4/2.0 + 15*m6/32.0 + 7*m8/16.0;
 a4 = m4/8.0 + 3*m6/16.0 + 7*m8/32.0;
 a6 = m6/32.0 + m8/16.0;

 X = a0*B - sinB*cosB*( (a2-a4+a6) + (2*a4-(16*a6/3))*sinB*sinB + 16*a6*Math.pow(sinB, 4)/3.0 );

其中e1为椭球第一偏心率。

反算公式

高斯投影反算有两种计算方式，一种是直接算法，另一种是设定初值迭代计算。这里主要说明一下迭代算法：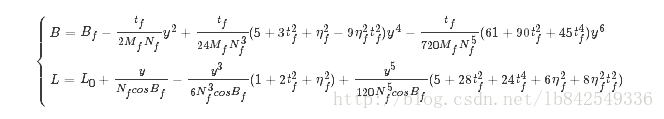

其中，Bf为底点纬度，即当x=X（子午线弧长）时对应的纬度，因此可以按照子午线弧长公式进行迭代。
设初始值

则按照如下公式进行迭代：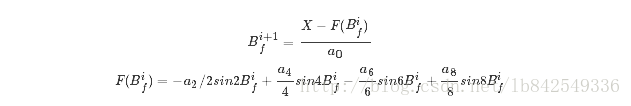

重复迭代直到差值小于ε
关于一些中间参数的计算：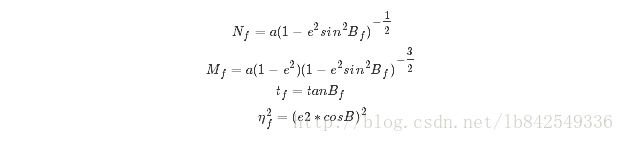

给出正反算的代码：

/**
  * 高斯投影正算
  * @param coord 要正算的坐标
  * @param pcs 投影坐标系
  * @param L0 中央经线
  * @return
  */
 public Coordinate gaussBL2XY(Coordinate coord, ProjectCoordinateSystem pcs, double L0){
     Coordinate newCoord = new Coordinate();
     double B = Math.toRadians(coord.X);
     double L = Math.toRadians(coord.Y);

     // 计算相关中间参数
     double a, e1, e2;
     double m0, m2, m4, m6, m8;
     double a0, a2, a4, a6;
     double X;
     double l;
     double N, W;
     double ita2, T, sinB, cosB;

     a = pcs.GCS.referenceSpheroid.semimajorAxis;             //长半轴
     e1 = pcs.GCS.referenceSpheroid.getFirstEccentricity();   //第一偏心率
     e2 = pcs.GCS.referenceSpheroid.getSecondEccentricity();  //第二偏心率
     ita2 = e2*e2*Math.cos(B)*Math.cos(B);
     sinB = Math.sin(B);
     cosB = Math.cos(B);
     l = L - Math.toRadians(L0);
     W = Math.sqrt(1-e1*e1*sinB*sinB);
     N = a/W;
     T = Math.tan(B) * Math.tan(B);

     m0 = a * (1 - e1*e1);
     m2 = 3 * (e1 * e1 * m0) / 2.0;
     m4 = 5 * (e1 * e1 * m2) / 4.0;
     m6 = 7 * (e1 * e1 * m4) / 6.0;
     m8 = 9 * (e1 * e1 * m6) / 8.0;

     a0 = m0 + m2/2.0 + 3*m4/8.0 + 5*m6/16.0 + 35*m8/128.0;
     a2 = m2/2.0 + m4/2.0 + 15*m6/32.0 + 7*m8/16.0;
     a4 = m4/8.0 + 3*m6/16.0 + 7*m8/32.0;
     a6 = m6/32.0 + m8/16.0;

     X = a0*B - sinB*cosB*(
             (a2-a4+a6) + (2*a4-(16*a6/3))*sinB*sinB + 16*a6*Math.pow(sinB, 4)/3.0
             );

     newCoord.X = X + N*sinB*cosB*l*l/2.0
                + N*sinB*cosB*cosB*cosB*(5-T+9*ita2+4*ita2*ita2)*l*l*l*l/24.0
                + N*sinB*cosB*cosB*cosB*cosB*cosB*(61-58*T+T*T)*l*l*l*l*l*l/720.0;

     newCoord.Y = N*cosB*l
                + N*cosB*cosB*cosB*(1-T+ita2)*l*l*l/6.0
                + N*cosB*cosB*cosB*cosB*cosB*(5-18*T+T*T+14*ita2-58*ita2*T)*l*l*l*l*l/120.0;

     // 加入尺寸变化和坐标轴偏移量
     newCoord.X = newCoord.X*pcs.projectParameter.scale;
     newCoord.Y = newCoord.Y*pcs.projectParameter.scale;
     newCoord.X += pcs.projectParameter.offsetX;
     newCoord.Y += pcs.projectParameter.offsetY;
     newCoord.Z = 0;

     return newCoord;
 }
/**
  * 高斯投影反算
  * @param coord 要反算的坐标
  * @param referenceSpheroid 参考椭球体
  * @param L0 中央经线
  * @return 返回计算结果
  */
 public Coordinate gaussXY2BL(Coordinate coord, ProjectCoordinateSystem pcs, double L0){
     Coordinate newCoord = new Coordinate();
     // 反算坐标偏移和尺度变换
     double x = coord.X - pcs.projectParameter.OffsetX;
     double y = coord.Y - pcs.projectParameter.OffsetY;
     x = x/pcs.projectParameter.Scale;
     y = y/pcs.projectParameter.Scale;

     // 计算相关中间参数
     double e1Pow2;
     double e2Pow2;
     double m0, m2, m4, m6, m8;
     double a0, a2, a4, a6, a8;
     double Nf, Mf, Wf;
     double a;
     double n2;
     double cosBf, sinBf, tanBf;

     a = pcs.GCS.referenceSpheroid.SemimajorAxis;
     e1Pow2 = pcs.GCS.referenceSpheroid.GetFirstEccentricityPow2();
     e2Pow2 = pcs.GCS.referenceSpheroid.GetSecondEccentricityPow2();

     m0 = a * (1 - e1Pow2);
     m2 = 3 * e1Pow2 * m0 / 2;
     m4 = 5 * e1Pow2 * m2 / 4;
     m6 = 7 * e1Pow2 * m4 / 6;
     m8 = 9 * e1Pow2 * m6 / 8;

     a0 = m0 + m2/2 + 3/8*m4 + 5/16*m6 + 35/128*m8;
     a2 = m2/2 + m4/2 + 15/32*m6 + 7/16*m8;
     a4 = m4/8 + 3/16*m6 + 7/32*m8;
     a6 = m6/32 + m8/16;
     a8 = m8/128;

     // 迭代计算Bf（底点纬度）
     double Bf;
     double Bfi1 = x/a0;
     double Bfi0 = Bfi1;
     double FBi;

     boolean isMin = false;
     int count = 0;   //限制最多迭代30次
     do{
         Bfi0 = Bfi1;
         FBi = 0.0 - a2*Math.sin(2*Bfi0)/2 + a4*Math.sin(4*Bfi0)/4 - a6*Math.sin(6*Bfi0)/6 + a8*Math.sin(8*Bfi0)/8;
         Bfi1 = (x - FBi) / a0;

         if(Math.abs(Bfi1-Bfi0) < (Math.PI * Math.pow(10.0,-8)/(36*18))){
             isMin = true;
         }
         count++;
     }
     while(!isMin && count < 30); 

     Bf = Bfi1;
     Nf = a / Math.sqrt((1 - e1Pow2 * Math.sin(Bf) * Math.sin(Bf)));
     cosBf = Math.cos(Bf);
     sinBf = Math.sin(Bf);
     tanBf = Math.tan(Bf);
     Wf = Math.sqrt(1 - e1Pow2*sinBf*sinBf);
     Nf = a / Wf;
     Mf = a*(1 - e1Pow2)/(Wf*Wf*Wf);
     n2 = e2Pow2*cosBf*cosBf;

     newCoord.X = Bf 
        - tanBf/(2*Mf*Nf)*y*y 
        + tanBf/(24*Mf*Math.pow(Nf, 3))*(5+3*tanBf*tanBf+n2-9*n2*tanBf*tanBf)*Math.pow(y, 4)
        - tanBf/(720*Mf*Math.pow(Nf, 5))*(61+90*tanBf*tanBf+45*Math.pow(tanBf, 4))*Math.pow(y, 6);

     newCoord.Y = y/(Nf*cosBf)
        - Math.pow(y, 3)/(6*Math.pow(Nf, 3)*cosBf)*(1+2*tanBf*tanBf+n2)
        + Math.pow(y, 5)/(120*Math.pow(Nf, 5)*cosBf)*(5+28*tanBf*tanBf+24*Math.pow(tanBf, 4)+6*n2+8*n2*tanBf*tanBf);
     newCoord.Y += Math.toRadians(L0);

     newCoord.X = Math.toDegrees(B);
     newCoord.Y = Math.toDegrees(L);
     return newCoord;
 } 

以上代码中的投影坐标系为自定义的数据结构，其中具体参数的计算同上面的公式介绍中一致。
第一次写博客，如有错误的地方还望指正。
ps转载请注明出处