数据结构——顺序表的初始化、插入、删除、查找、合并
目录
1、顺序表初始化
2、顺序表插入元素
3、顺序表删除元素
4、顺序表查找元素
5、顺序表合并
线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素。
顺序存储方式不仅只用于存储线性结构。
| 特点 | 优点 | 缺点 |
| 逻辑上相邻的数据元素物理存储位置也相邻, 并且顺序表的存储空间需要预先分配 |
1、方法简单,各级高中语言中都有数组,容易实现。 2、存储空间使用紧凑。 3、任一元素均可随机访问。 4、存储密度大。 |
1、插入和删除元素需要移动大量地元素,效率低。 2、表容量难以扩充。 3、预先分配空间需按最大空间分配,估计过大, 可能会导致顺序表后部大量闲置;估计过小,又会造成溢出。 |
//-------------------------线性表的动态分配顺序存储结构-------------------------//
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
ElemType *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
}SqList;在上述定义中,数组指针elem指示线性表的基地址;length指示线性表的当前长度;listsize指示顺序表当前分配的存储空间的大小,一旦因插入元素而空间不足时,可进行再分配,即为顺序表增加一个大小为存储LISTINCREMENT个数据元素的空间。
1、顺序表初始化
顺序表的初始化操作就是为顺序表分配一个预定义大小的数组空间,并将线性表的当前长度设为“0”。
#include
#include
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
int *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
}SqList;
int InitList_Sq(SqList *L)
{
L->elem = (int *)malloc(LIST_INIT_SIZE * sizeof(int)); //构造一个空的线性表L
if(!L->elem)
{
return -1; //存储分配失败(申请失败)
}
L->length = 0; //空表长度为 0
L->listsize = LIST_INIT_SIZE; //初始存储容量
return 1;
}
int main()
{
SqList L; //声明一个顺序表
InitList_Sq(&L); //初始化
for(int i=0; i<10; i++) //将顺序表的前10个单元赋值为0~9,
{
L.elem[i] = i;
L.length++;
printf("%d ", L.elem[i]);
}
}
'''
结果:
0 1 2 3 4 5 6 7 8 9
''' 2、顺序表插入元素
在顺序存储结构中,插入和删除元素,需要大量地移动元素,所有效率低。
在顺序表插入和删除元素,最主要的操作时移动元素。
要在第 i (1<=i<=n)个元素之前插入元素,共n-i+1个元素依次向后移一个位置。
| 插入下标位置 i | 0 | 1 | 2 | ··· | i | ··· | n-1 | n |
| 移动次数 | n | n-1 | n-1 | ··· | n-i | ··· | 1 | 0 |
若长度为n的线性表采用顺序存储结构,在其第 i 个位置插入一个新元素的算法时间复杂度为O(n)
若i = n,算法时间复杂度为O(1)
#include
#include
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
int *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
}SqList;
int InitList_Sq(SqList *L)
{
L->elem = (int *)malloc(LIST_INIT_SIZE * sizeof(int)); //构造一个空的线性表L
if(!L->elem)
{
return -1; //存储分配失败(申请失败)
}
L->length = 0; //空表长度为 0
L->listsize = LIST_INIT_SIZE; //初始存储容量
return 1;
}
int ListInsert_Sq(SqList *L, int i, int e) //在顺序表的第i个位置插入元素e
{
//i的范围区间[1, ListLength_Sq(L)+1]
if(i<1 || i>L->length+1)
{
return -1; //i的值不合法
}
if(L->length >= L->listsize) //存储空间=分配空间,空间已满,增加分配
{
int *newbase = (int *)realloc(L->elem, (L->listsize+LISTINCREMENT) * sizeof(int));
if(!newbase)
{
return -1; //存储分配失败
}
L->elem = newbase; //新基址
L->listsize += LISTINCREMENT; //增加存储容量
}
int *q = &(L->elem[i-1]); //q为插入的位置
for (int *p=&(L->elem[L->length-1]); p>=q; --p) //p为最后一个位置,用来移动元素
{
*(p+1) = *p; //插入位置及之后的元素右移
}
*q = e; //插入元素e
++L->length; //表长增1
return 1;
}
int main()
{
SqList L; //声明一个顺序表
InitList_Sq(&L); //初始化
for(int i=1; i<=10; i++) //空表中,逐个插入1~10
{
ListInsert_Sq(&L, i, i);
}
for(int i=0; i<10; i++) //遍历、打印
{
printf("%d ", L.elem[i]);
}
}
'''
结果:
1 2 3 4 5 6 7 8 9 10
''' 3、顺序表删除元素
| 删除下标位置 i | 0 | 1 | 2 | ··· | i | ··· | n-2 | n-1 |
| 移动次数 | n-1 | n-2 | n-3 | ··· | n-i+1 | ··· | 1 | 0 |
若长度为n的线性表采用顺序存储结构,在其第 i 个位置删除一个元素的算法时间复杂度为O(n)
若i = n-1,算法时间复杂度为O(1)
#include
#include
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
int *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
}SqList;
int InitList_Sq(SqList *L)
{
L->elem = (int *)malloc(LIST_INIT_SIZE * sizeof(int)); //构造一个空的线性表L
if(!L->elem)
{
return -1; //存储分配失败(申请失败)
}
L->length = 0; //空表长度为 0
L->listsize = LIST_INIT_SIZE; //初始存储容量
return 1;
}
int ListDelete_Sq(SqList *L, int i, int *e) //在顺序表L中删除第i个元素,用e返回其值
{
//i的范围区间[1, ListLength_Sq(L)+1]
if(i<1 || i>L->length)
{
return -1; //i值不合法
}
int *p = &(L->elem[i-1]); //指针p指向被删除元素的位置
*e = *p; //被删除的元素赋值给e
int *q = &(L->elem[L->length-1]); //指针p指向表尾元素的位置
for(++p; p<=q; ++p)
{
*(p-1) = *p; //被删除元素之后的元素左移
}
--L->length; //表长减1
return 1;
}
int main()
{
SqList L; //声明一个顺序表
InitList_Sq(&L); //初始化
for(int i=0; i<10; i++)
{
L.elem[i] = i; //空表中,逐个赋值0~9
printf("%d ", L.elem[i]);
L.length++;
}
printf("\n");
int e = 0;
ListDelete_Sq(&L, 6, &e);
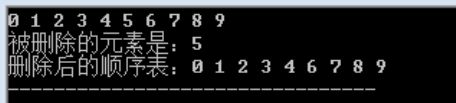
printf("被删除的元素是:%d\n", e);
printf("删除后的顺序表:");
for(int i=0; i<9; i++)
{
printf("%d ", L.elem[i]);
}
} 结果:
4、顺序表查找元素
(查找线性表中给定值key的位序)
#include
#include
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
int *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
}SqList;
int InitList_Sq(SqList *L)
{
L->elem = (int *)malloc(LIST_INIT_SIZE * sizeof(int)); //构造一个空的线性表L
if(!L->elem)
{
return -1; //存储分配失败(申请失败)
}
L->length = 0; //空表长度为 0
L->listsize = LIST_INIT_SIZE; //初始存储容量
return 1;
}
int LocateElem_Sq(SqList *L, int key) //在顺序表L中查找key的位序
{
int i=1;
int *p = &(L->elem[0]); //指针p指向表头的位置
while(i<=L->length && (*p!=key))
{
p++;
i++;
}
if(i < L->length)
return i; //返回key的位序
else
return 0; //未找到
}
int main()
{
SqList L; //声明一个顺序表
InitList_Sq(&L); //初始化
for(int i=0; i<10; i++)
{
L.elem[i] = i; //空表中,逐个赋值0~9
printf("%d ", L.elem[i]);
L.length++;
}
printf("\n");
int key = 5;
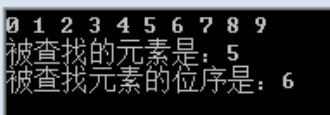
printf("被查找的元素是:%d\n", key);
printf("被查找元素的位序是:%d\n", LocateElem_Sq(&L, key));
}
结果:
5、顺序表合并
#include
#include
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
#define LISTINCREMENT 10 //线性表存储空间的分配增量
typedef struct{
int *elem; //存储空间基址
int length; //当前长度
int listsize; //当前分配的存储容量(以sizeof(ElemType)为单位)
}SqList;
int InitList_Sq(SqList *L)
{
L->elem = (int *)malloc(LIST_INIT_SIZE * sizeof(int)); //构造一个空的线性表L
if(!L->elem)
{
return -1; //存储分配失败(申请失败)
}
L->length = 0; //空表长度为 0
L->listsize = LIST_INIT_SIZE; //初始存储容量
return 1;
}
//线性表La、Lb中元素按值非递减排列,La、Lb合并为新线性表Lc,Lc中元素也是按值非递减排列。
int MergeList_Sq(SqList *La, SqList *Lb, SqList *Lc)
{
int *pa = &(La->elem[0]); //指针pa指向La表头的位置
int *pb = &(Lb->elem[0]); //指针pb指向Lb表头的位置
Lc->listsize = Lc->length = La->length+Lb->length; //初始化Lc
int *pc = Lc->elem = (int *)malloc(Lc->listsize*sizeof(int)); //给Lc分配空间
if(!Lc->elem)
{
return -1; //存储分配失败(申请失败)
}
int *pa_last = &(La->elem[La->length-1]); //指针pa_last指向La表尾的位置
int *pb_last = &(Lb->elem[Lb->length-1]); //指针pb_last指向Lb表尾的位置
while(pa<=pa_last && pb<=pb_last) //归并
{
if(*pa <= *pb)
{
*pc = *pa;
pc++;
pa++;
}
else
{
*pc = *pb;
pc++;
pb++;
}
}
while(pa <= pa_last) //插入La的剩余元素
{
*pc = *pa;
pc++;
pa++;
}
while(pb <= pb_last) //插入Lb的剩余元素
{
*pc = *pb;
pc++;
pb++;
}
return 0;
}
int main()
{
SqList La, Lb, Lc; //声明3个线性表
InitList_Sq(&La); //初始化线性表La
InitList_Sq(&Lb); //初始化线性表Lb
La.elem[0]=2; La.elem[1]=5; La.elem[2]=5;
La.elem[3]=7; La.elem[4]=8; La.elem[5]=9;
La.length = 6;
Lb.elem[0]=1; Lb.elem[1]=2; Lb.elem[2]=4;
Lb.elem[3]=6; Lb.elem[4]=6; Lb.elem[5]=9;
Lb.length = 6;
MergeList_Sq(&La, &Lb, &Lc);
printf("线性表La的元素:");
for(int i=0; i<6; i++)
{
printf("%d ", La.elem[i]);
}
printf("\n");
printf("线性表Lb的元素:");
for(int i=0; i<6; i++)
{
printf("%d ", Lb.elem[i]);
}
printf("\n");
printf("合并后线性表Lc的元素:");
for(int i=0; i<12; i++)
{
printf("%d ", Lc.elem[i]);
}
} 结果: