OpenGL.ES在Android上的简单实践：4-曲棍球（正交投影解决横屏变形）

OpenGL.ES在Android上的简单实践：4-曲棍球（正交投影解决横屏变形）

 

你可能还没注意到曲棍球桌子在横屏的时候是怎样的龌蹉难看。不信你看看：

桌子在横屏模式情况下被压扁了，这之所以会发生，是因为我们之前直接把坐标传递給OpenGL，但OpenGL在每个屏幕上都是归一化坐标系，没有考虑屏幕的宽高比。那么怎么处理科学的处理这个问题呢？

一个可行的方法就是把较小的范围固定在 [-1,1]内，而按屏幕尺寸的比例调整较大的范围。 举例来说，在竖屏情况下，其宽度是720， 而高度是1280，因此我们可以把宽度范围限定在 [-1,1]，并把高度范围调整为 [-1280/720, 1280/720]或 [-1.78,1.78]。横屏的时候同理，把宽度范围设为 [-1.78,1.78]，而高度范围控制在 [-1,1]。

在OpenGL开发团队肯定是能预料到的，以上方法（调整坐标空间）虽然能解决问题，但是从性能/编码程度来看，都不是一般的烦，那要怎么办？首先，我们需要停止直接在归一化设备坐标上工作，而开始在虚拟坐标空间里工作，紧接着，把虚拟坐标转换回归一化设备坐标的方法，这种转换应该把屏幕方向计算在内。以上操作我们称之为正交投影（ortho graphic projection）。

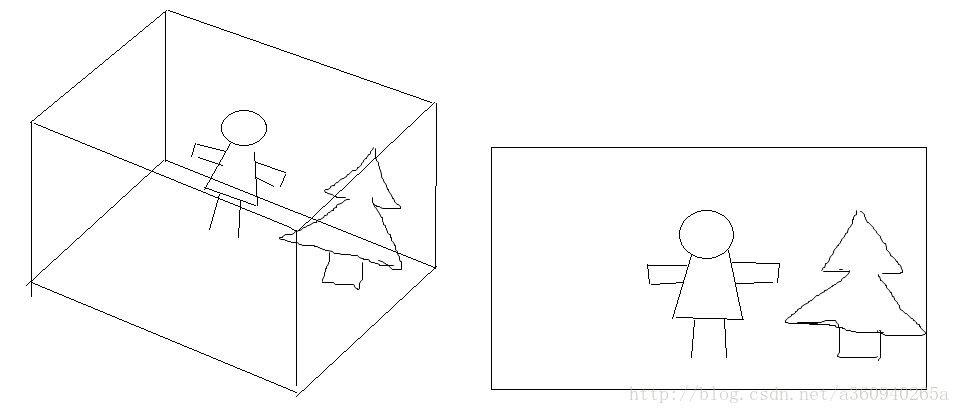
当我们使用正交投影把虚拟坐标变换回归一化设备坐标时，实际上定义了三维世界内部的一个区域，在这个区域的所有东西都会显示在屏幕上，而区域外的都会被裁剪。下面一幅来自灵魂画师的图，我们能在一个封闭的立方体内看到一个女孩和一棵树。当我们使用正交投影矩阵把这个立方体映射到屏幕上时，就会看到女孩和树的正照了。

利用正交投影矩阵改变立方体的大小，以使我们可以在屏幕上看到或多或少的场景，也能改变弥补屏幕的宽高比的影响。

 

OpenGL大量使用了向量和矩阵，矩阵的最重要的用途之一就是建立正交投影，和往后会学到的透视投影。其原因之一是，从本质上来说，使用矩阵做投影只涉及对一组数据按顺序执行大量的加法和乘法。回顾大学时代的线性代数，如果不太记得了，请到这里（矩阵数学）复习一下，一旦理解了这些基础的线性代数，就可以开始学习如何用矩阵做正交投影了。

我们将使用android.opengl.Matrix的orthoM方法定义生成一个正交投影。我们来看看orthoM的所有参数：

 

orthoM(float[] m, int mOffset, float left, float right, float bottom, float top, float near, float far)

float[] m：目标数组，这个数组的长度至少有16个元素，这样才能储存正交投影。
int mOffset：结果矩阵起始的偏移值。
float left：x轴的最小范围
float right：x轴的最大范围
float bottom：y轴的最小范围
float top：y轴的最大范围
float near：z轴的最小范围
float far：z轴的最大范围
当我们调用这个方法的时候，它应该产生下面的正交投影矩阵：

 

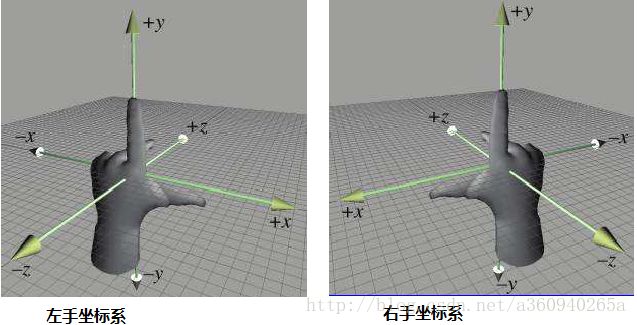
注意到z轴上的值有一个负号，它的效果是翻转z坐标。这就意味着，物体离得越远，z坐标的负值会越来越小。这说明什么？这是历史和传统的缘故，这里（左手与右手坐标系统）作出讲解，我们现在只需要知道结论就好了。因为Android上的OpenGL默认是使用右手坐标系的。（Direct3D使用的是左手坐标系）

好了，说了那么多废话，让我们现在更新代码吧。首先从着色器开始，我们更新simple_vertex_shader.glsl。

 

uniform mat4 u_Matrix;

attribute vec4 a_Position;
attribute vec4 a_Color;

varying vec4 v_Color;

void main()
{
    v_Color = a_Color;
    gl_Position = u_Matrix * a_Position;
    gl_PointSize = 20.0;
}gl_Position = u_Matrix * a_Position;
    gl_PointSize = 20.0;
}

我们添加了一个新的uniform定义“u_Matrix”，并把它定义为一个mat4类型，意思是这个uniform代表一个4*4的矩阵，随后我们把这个矩阵与传递的位置进行相乘。这意味着顶点数组不用再被翻译为归一化设备坐标了，其将理解为存在于正交矩阵所定义的虚拟坐标空间中。（重点）然后通过正交矩阵把坐标从虚拟坐标空间变换归一化设备坐标。

 

我们回到Renderer中，添加获取u_Matrix属性的模板代码：

 

private static final String U_MATRIX = "u_Matrix";
private int uMatrixLocation;

@Override
public void onSurfaceCreated(GL10 gl10, EGLConfig eglConfig) {
       ... ...
       uMatrixLocation = GLES20.glGetUniformLocation(programId, U_MATRIX);

}

下一步就是创建正交投影矩阵，我们在onSurfaceChanged()更新代码：

 

 

    @Override
    public void onSurfaceChanged(GL10 gl10, int width, int height) {
        GLES20.glViewport(0,0,width,height);

        final float aspectRatio = width > height ?
                (float)width / (float)height   :
                (float)height / (float)width ;
        if(width > height){
            Matrix.orthoM(projectionMatrix,0, -aspectRatio, aspectRatio,   -1f,1f,    -1f,1f);
        } else {
            Matrix.orthoM(projectionMatrix,0, -1f,1f,    -aspectRatio, aspectRatio,   -1f,1f);
        }
    }

好了，就差一步，我们在onDrawFrame把正交矩阵传到着色器

@Override
    public void onDrawFrame(GL10 gl10) {
        GLES20.glClear(GLES20.GL_COLOR_BUFFER_BIT);

        GLES20.glUniformMatrix4fv(uMatrixLocation,1, false,  projectionMatrix,0);
        ... ...
    }

运行程序，观察竖屏横屏的桌子吧。

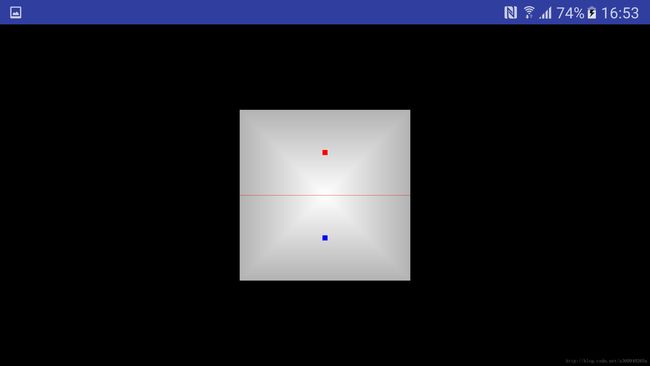
额，横屏是没压扁了，但是怎么感觉不太对劲，长方桌子怎么变成了正方形了。还记得上边红色加粗的重点吗？我们还没修改顶点数据呢！让我们更新桌子的结构，让y轴拉伸（0.5->0.8）。

 

 

float[] tableVerticesWithTriangles = {
            // X, Y, R, G, B
            // 三角扇
             0,     0,     1f, 1f, 1f,
            -0.5f, -0.8f,  0.7f,0.7f,0.7f,
             0.5f, -0.8f,  0.7f,0.7f,0.7f,
             0.5f,  0.8f,  0.7f,0.7f,0.7f,
            -0.5f,  0.8f,  0.7f,0.7f,0.7f,
            -0.5f, -0.8f,  0.7f,0.7f,0.7f,
            // 中间的分界线
            -0.5f,  0f,    1f,0f,0f,
             0.5f,  0f,    1f,0f,0f,
            // 两个木槌的质点位置
             0f,   -0.4f,  0f,0f,1f,
             0f,    0.4f,  1f,0f,0f,
    };

大家自己去观察运行结果吧。 _(¦3」∠)_
 

 

小结：
        这节内容不多，我们引入了正交投影来解决屏幕长宽比例改变后，坐标归一化的问题。重点是，顶点数组不用再被直接设置为归一化设备坐标了，而是将其理解为存在于正交矩阵所定义的虚拟坐标空间中。