论文笔记《DeepWalk: Online Learning of Social Representations》

摘要

我们提出了DeepWalk，这是一种用于学习网络中顶点的隐表示的新颖方法。这些隐表征将社会关系编码在一个连续的向量空间中，这很容易被统计模型利用。 Deep-Walk 概括了语言建模和无监督特征学习(或深度学习)方面的最新进展，从单词序列到图形。
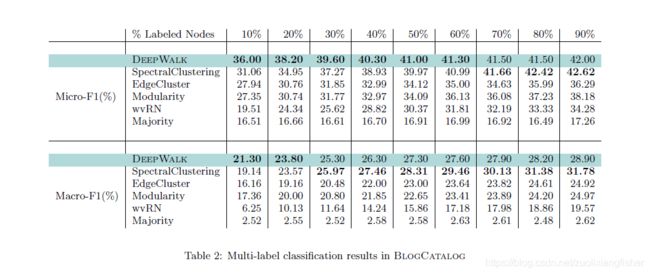
DeepWalk使用从截断的随机游走中获得的局部信息，通过将游走视为句子的等效词来学习潜在表示。我们演示了Deep-Walk在社交网络（例如BlogCatalog，Flickr和YouTube）的多个多标签网络分类任务中的潜在表示形式。我们的结果表明，DeepWalk的性能优于具有挑战性的基准，这使网络可以全局查看，尤其是在缺少信息的情况下。当标记的数据稀疏时，DeepWalk的表示形式可以提供比竞争方法高10％的F1分数。在某些实验中，DeepWalk的表示能够胜过所有基线方法，而使用的训练数据却少60％。 DeepWalk也是可扩展的。这是一种在线学习算法
可以建立有用的增量结果，并且可以并行化。这些品质使其适用于各种实际应用，例如网络分类和异常检测。

1、简介

文章的贡献如下：

• 我们将深度学习介绍为一种分析图形的工具，以构建适用于统计建模的强大表示形式。 DeepWalk学习短时随机游走中存在的结构规律。
• 我们广泛评估了我们在多个社交网络上对多标签分类任务的表示形式。 我们发现，在存在标签稀疏性的情况下，分类性能显着提高，在我们考虑的最稀疏问题上，Micro F1的改进率为5％-10％。 在某些情况下，即使仅提供少60％的培训数据，DeepWalk的表现仍能胜过竞争对手。
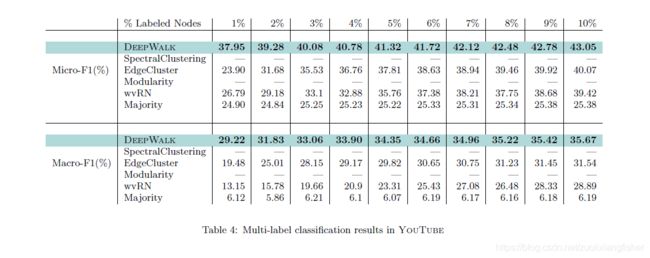
• 我们通过使用并行实现构建Web规模图的表示形式（例如YouTube），展示了算法的可扩展性。 而且，我们描述了构建我们的方法的流版本所需的最小更改。

2、问题定义

我们考虑的问题是将社交网络中的成员分为单个或者多个类目标签。令 $G=(V,E)$，其中 $V$ 代表 网络中的节点， $E$ 表示连接的边 $E\subseteq (V,V)$，$G_L=(V,E,X,Y)$ 是部分带标签网络，属性 $X\in {\mathbb{R}}^{|V|\times S}$， $S$ 是特征空间中每个属性向量的大小，$Y\in {\mathbb{R}}^{|V|\times \mathcal{Y}}$，$\mathcal{Y}$ 是标签集合。
传统的机器学习中，我们的目标是学习一个假设 $H$，将特征集合 $X$ 映射到标签集合 $\mathcal{Y}$ 上，在我们的案例中，我们可以利用有关嵌入在 $G$ 结构中的示例的相关性的重要信息来实现出色的性能。
在文献中，这被称为关系分类（或集体分类问题[37]）。传统的关系分类方法将问题作为无向马尔可夫网络中的推理提出，然后使用迭代近似推理算法（例如迭代分类算法[32]，Gibbs Sampling [15]或标签松弛[19]）给定网络结构，计算标签的后验分布。
我们提出了一种不同的方法来捕获网络拓扑信息。与其将标签空间作为特征空间的一部分进行混合，我们提出了一种不受监督的方法，该方法可学习捕获与标签分布无关的图形结构的特征。
结构表示和标记任务之间的这种分离避免了级联错误，该级联错误可能在迭代方法中发生[34]。而且，相同的表示可以用于与该网络有关的多个分类问题。
我们的目标是学习 $X_E\in {\mathbb{R}}^{|V|\times d}$，其中 $d$ 是较小的隐维数。 这些低维表示形式是分布式的。 意思是每个社会现象都由维度的一个子集表达，每个维度都对空间表达的社会概念的一个子集有所贡献。
使用这些结构特征，我们将扩大属性空间以帮助分类决策。 这些功能是通用的，可以与任何分类算法（包括迭代方法）一起使用。 但是，我们认为这些功能的最大用途是易于与简单的机器学习算法集成。 它们将在现实世界的网络中适当扩展，如我们将在第6节中所示。

3、学习社交表征

我们寻求学习具有以下特征的社交表征

• 适应性 真实的社交网络在不断发展； 新的社会关系不应要求重复学习过程
• 社区意识 潜在维度之间的距离应代表用于评估网络相应成员之间的社会相似性的度量。 这允许具有同构性的网络泛化。
• 低维 当缺乏标签数据时，低维模型可以更好地泛化，并加快收敛和推理速度。
• 连续的 我们需要潜在的表示来对连续空间中的部分社区成员进行建模。 除了提供社区成员细微差别的视图外，连续的表示形式在社区之间具有平滑的决策边界，从而可以实现更可靠的分类。

我们的方法通过使用最初为语言建模设计的优化技术，从一小段随机游走中学习顶点的表示形式，从而满足了这些要求。 在这里，我们回顾了随机游走和语言建模的基础知识，并描述了它们的组合如何满足我们的要求。

3.1 随机游走

我们将根源于顶点 $v_i$ 的随机游走表示为 ${\mathcal{W}}_{v_i}$。它是具有随机变量 ${\mathcal{W}}_{v_i}^1,{\mathcal{W}}_{v_i}^2,...,{\mathcal{W}}_{v_i}^k$ 的随机过程。 这样 ${\mathcal{W}}_{v_i}^{k+1}$是从顶点 $v_k$ 的邻居中随机选择的一个顶点。随机游走已被用作内容推荐[12]和社区检测[2]中各种问题的相似性度量。它们也是一类输出敏感算法的基础，该算法使用它们在时间上与输入图的大小成线性关系计算本地社区结构信息[38]。
正是这种与本地结构的联系促使我们使用短随机游走流作为我们从网络提取信息的基本工具。除了捕获社区信息之外，使用随机游走作为我们算法的基础还为我们提供了两个其他理想的属性。首先，本地勘探很容易并行化。几个随机游走者（在不同的线程，进程或机器中）可以同时浏览同一图形的不同部分。其次，依靠从短距离随机游走中获得的信息，可以适应图结构中的细微变化，而无需全局重新计算。我们可以用新的随机游程迭代地更新学习的模型，该随机游程从变化的区域按时间线性变化到整个图形。

3.2 连接：幂定律(power laws)

选择在线随机游走作为捕获图结构的原始方法之后，我们现在需要一种合适的方法来捕获此信息。如果连接图的度数分布遵循幂定律（即无标度），则我们观察到在短随机游走中顶点出现的频率也将遵循幂律分布。
自然语言中的单词频率遵循相似的分布，并且来自语言建模的技术解释了这种分布行为。为了强调这种相似性，我们在图2中显示了两个不同的幂律分布。第一个来自无标度图上的一系列短随机游动，第二个来自英语Wikipedia的100,000条文章。
我们工作的核心贡献在于，可以将用于建模自然语言（符号频率遵循幂律分布（或齐普夫定律）的模型）的技术重新用于建模网络中的社区结构。我们将在本节的其余部分中回顾语言建模方面不断发展的工作，并将其转换为学习满足我们标准的顶点表示。

3.3 语言模型

语言建模的目的是估计单词在语料库中出现特定序列的可能性。 更正式地说，给定一个单词序列 $W_1^n=(w_0,w_1,...,w_n)$，其中 $w_i\in \mathcal{V}$($\mathcal{V}$是词汇量)，我们希望在所有训练语料库上最大化 $\mathrm{P}\mathrm{r}(w_n|w_0,w_1,...,w_{n-1})$。表示学习的最新工作集中在使用概率神经网络来构建单词的一般表示，这将语言建模的范围扩展到了其最初的目标之外。
在这项工作中，我们提出了一种语言建模的一般化方法，以通过一系列简短的随机游走探索图。 这些步行可以被认为是特殊语言中的简短句子和短语。 直接的模拟是在给定的随机游走中迄今访问过的所有先前顶点的情况下估计观察顶点 $v_i$ 的可能性。$$\mathrm{P}\mathrm{r}(v_n|(v_0,v_1,...,v_{n-1}))\text{\hspace{1em}(1)}$$
我们的目标是学习潜在的表征，而不仅仅是节点共现的概率分布，因此我们引入了一个映射函数：$\Phi :v\in \mathcal{V}\to {\mathbb{R}}^{|V|\times d}$该映射表示与图中每个顶点 $v$ 相关的隐社交表征。(实际上，我们用一个自由参数的 $|V|\times d$ 的矩阵表示 $\Phi$，以后将用作我们的 $X_E$）。 然后，问题就是估计可能性：$$\mathrm{P}\mathrm{r}(v_n|(\Phi (v_0),\Phi (v_1),...,\Phi (v_{n-1})))\text{\hspace{1em}(2)}$$ 但是随着游走长度的增加，计算这个条件概率变得不可行。语言建模的最新松弛[27，28]使预测问题在最开始的时候做了转变。 首先，它不是使用上下文来预测缺失的单词，而是使用一个单词来预测上下文。 其次，上下文由出现在给定单词左右两侧的单词组成。 最后，它消除了对问题的排序约束，而是要求模型最大化任何单词在上下文中出现的概率，而无需从给定单词知道它的集合。 在顶点表示建模方面，这产生了优化问题 $$\underset{\Phi }{\min }-\mathrm{P}\mathrm{r}(\{v_{i-w,...,v_{i+w}}\}\setminus v_i|\Phi (v_i))\text{\hspace{1em}(3)}$$我们发现，这些松弛对于社交表征学习尤为可取。 首先，顺序独立性假设可以更好地捕捉随机游走所提供的“近距离感”。 此外，这种松弛对于通过一次建立一个顶点来构建小模型来加快训练时间非常有用。
等式(3)中解决优化问题，即建立了捕获顶点之间局部图结构中共享相似性的表征。 具有相似邻域的顶点将获得相似的表征（对共引文相似性进行编码），从而可以对机器学习任务进行概括。
通过结合截断的随机游走和语言模型，我们制定了一种满足我们所有期望属性的方法。 此方法生成低维的社交网络表征，并存在于连续向量空间中。 它的表征编码了社区成员关系的潜在形式，并且由于该方法输出有用的中间表征，因此它可以适应不断变化的网络拓扑。

4、方法

4.1 概览

像在任何语言建模算法中一样，唯一需要的输入是一个语料库和一个词汇表 $\mathcal{V}$。DeepWalk认为一组短截短的随机游走是它自己的语料库，而图顶点则是它自己的词汇表( $\mathcal{V}$ = $V$)。 虽然了解 $V$ 和随机中顶点的频率分布在训练之前是有益的，但正如我们在4.2.2中所示，算法在工作中其实没必要了解

4.2 算法：深度游走

算法主要由两部分组成，首先是随机游走生成器，其次是一个更新过程。随机游走生成器以图 $G$ 作为输入，随机采样一个节点 $v_i$ 作为随机游走序列 ${\mathcal{W}}_{v_i}$ 的根节点。一个游走从最近的节点开始随机采样，直到达到最大长度 ($t$)，在实验中我们对随机游走的长度设了一个固定值，当然没有严格的限制要求必须是一样长短，这些游走可以从头开始(返回根节点)，但是我们的初步结果并未显示使用重启(返回根节点)的任何优势。 在实践中，我们的实现指定了 $\gamma$ 个长度为 $t$ 的随机游动从每个顶点开始。

算法 1 中的3-9行显示了我们方法的核心，外循环确定了次数 $\gamma$，我们应该在每个顶点处开始随机游走。 我们认为每次迭代都是对数据进行“遍历”，并在此遍历中对每个节点进行一次遍历。 在每次遍历的开始，我们都会生成一个随机排序以遍历顶点。 这不是严格要求的，但众所周知，它可以加快随机梯度下降的收敛速度。
在内循环里，我们循环遍历图中所有的节点，对于每个顶点 $v_i$，生成一个游走序列 $|{\mathcal{W}}_{v_i}|$=$t$，然后第7行中用它来更新我们的表征，我们根据等式 (3) 中的目标函数，使用SkipGram算法 [27] 更新这些表征。

4.2.1 SkipGram

SkipGram是一种语言模型，可最大程度地提高出现在窗口 $w$ 中句子中的单词之间的共现概率。 它使用以下独立性假设来近似公式3中的条件概率 $$\mathrm{P}\mathrm{r}(\{v_{i-w,...,v_{i+w}}\}\setminus v_i|\Phi (v_i))=\prod _{j=i-w,j\ne i}^{i+w}\mathrm{P}\mathrm{r}(v_j|\Phi (v_i))\text{\hspace{1em}(4)}$$

算法2迭代出现在窗口 $w$（第1-2行）中的随机游走中所有可能的组合。 对于每个顶点，我们将每个顶点 $v_j$ 映射到其当前表征向量 $\Phi (v_j)\in {\mathbb{R}}^d$（请参见图3b）。 给定 $v_j$ 的表示形式，我们希望最大化其在步行中的邻居的概率（第3行）。 我们可以使用几种分类器来学习这种后验分布。 例如，使用逻辑回归对先前的问题建模将导致大量的标签（等于 $|V|$ ），可能达数百万或数十亿。 这样的模型需要大量的计算资源，这些资源可能超过整个计算机集群[4]。 为了避免这种必要性并加快训练时间，我们改用Hierarchical
Softmax [40，31]来近似概率分布。

4.2.2 Hierarchical Softmax

给定 $u_k\in V$，计算 $\mathrm{P}\mathrm{r}(u_k|\Phi (v_j))$ 是不可行的，计算分区函数（归一化因子）非常昂贵，因此我们将使用分层softmax分解条件概率。 我们将顶点分配给二叉树的叶子，从而将预测问题转化为最大化层次结构中特定路径的概率（参见图3c）。 如果到顶点 $u_k$ 的路径由一系列树节点标识 $(b_0,b_1,...,b_{\lceil \log |V|\rceil })$, $(b_0=root,b_{\lceil \log |V|\rceil }=u_k)$，因此 $$\mathrm{P}\mathrm{r}(u_k|\Phi (v_j))=\prod _{l=1}^{\lceil \log |V|\rceil }\mathrm{P}\mathrm{r}(u_k|\Phi (v_j))\text{\hspace{1em}(5)}$$如等式6所示，$\mathrm{P}\mathrm{r}(u_k|\Phi (v_j))$ 可以由分配给节点 $b_l$的父节点的二进制分类器建模，$$\mathrm{P}\mathrm{r}(u_k|\Phi (v_j))=1/(1+e^{-\Phi (v_j)\cdot \Psi (b_l)})\text{\hspace{1em}(6)}$$其中 $\Psi (b_l)$ 是节点 $b_l$ 的父节点的表征，这样使得计算 $\mathrm{P}\mathrm{r}(u_k|\Phi (v_j))$ 的复杂度从 $O(|V|)$ 下降到 $O(\log |V|)$
通过为随机行走中的频繁顶点分配较短的路径，我们可以进一步加快训练过程。 霍夫曼编码用于减少树中频繁元素的访问时间。

4.2.3 优化

模型参数集为 $\theta =\{\Phi ,\Psi \}$，每个大小均为 $(d|V|)$，随机梯度下降（SGD）[5]用于优化这些参数（第4行，算法2）。 使用反向传播算法估计导数。 在训练开始时，SGD的学习率 $\alpha$ 最初设置为2.5％，然后根据到目前为止看到的顶点数量线性降低

4.3 并行化

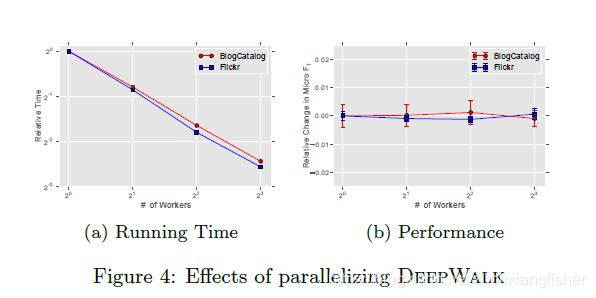
如图2所示，社交网络中随机游走的顶点的频率分布和语言中的单词都遵循幂律。这会导致很少出现的顶点的长尾情况，因此影响 $\Phi$ 的更新将很稀疏。在多woker的情况下，这使我们可以使用异步版本的随机梯度下降（ASGD）。鉴于我们的更新是稀疏的，并且我们没有获得访问模型共享参数的锁，因此ASGD将实现最佳收敛速度[36]。当我们在一台使用多线程的机器上运行实验时，已证明该技术具有高度的可扩展性，并且可以用于超大规模的机器学习[9]。图4展示了并行化DeepWalk的效果。它表明，随着我们将工作人员数量增加到8，处理BlogCatalog和Flickr网络的速度是一致的（图4a）。它还表明，相对于串行运行DeepWalk而言，预测性能没有损失（图4b）。

5、实验设计

5.1 数据集

• BlogCatalog
• Flick
• YouTube

5.2 Baseline 方法

• SpectralClustering [41]:
• Modularity [39]:
• EdgeCluster [40]:
• wvRN [25]:
• Majority:

原文链接：deepwalk