吴恩达深度学习 单隐藏层的2分类神经网络

我们要建立一个神经网络，它有一个隐藏层。

• 构建具有单隐藏层的2类分类神经网络。
• 使用具有非线性激活功能激活函数，例如tanh。
• 计算交叉熵损失（损失函数）。
• 实现向前和向后传播。

numpy：是用Python进行科学计算的基本软件包。
sklearn：为数据挖掘和数据分析提供的简单高效的工具。
matplotlib ：是一个用于在Python中绘制图表的库。
testCases：提供了一些测试示例来评估函数的正确性
planar_utils ：提供了在这个任务中使用的各种有用的功能

import numpy as np
import matplotlib.pyplot as plt
from testCases import *
from planar_utils import *
import sklearn
import sklearn.datasets
import sklearn.linear_model

np.random.seed(1)
X, Y = load_planar_dataset()
X.shape,Y.shape

(2,400), (1,400)
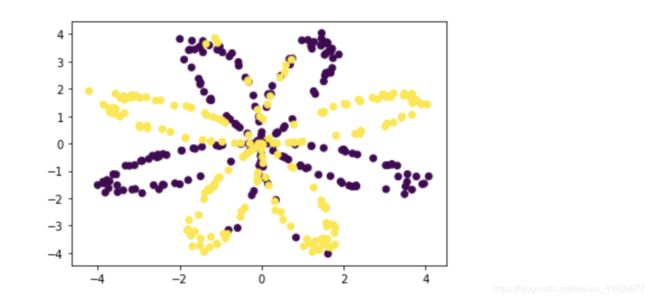
可视化观察一下数据的分布

plt.scatter(X[0,:],X[1,:],c=np.squeeze(Y))

注意⚠️，如果出现ValueError: ‘c’ argument has 1 elements, which is not acceptable for use with ‘x’ with size 400, ‘y’ with size 400.
是因为直接使用plt.scatter(X[0,:],X[1,:],Y)，需要np.squeeze(Y)，
squeeze 函数：从数组的形状中删除单维度条目，即把shape中为1的维度去掉

在构建完整的神经网络之前，先看看逻辑回归在这个问题上的表现如何，我们可以使用sklearn的内置函数来做到这一点， 运行下面的代码来训练数据集上的逻辑回归分类器。

model=sklearn.linear_model.LogisticRegression()
model.fit(X.T,Y.T)
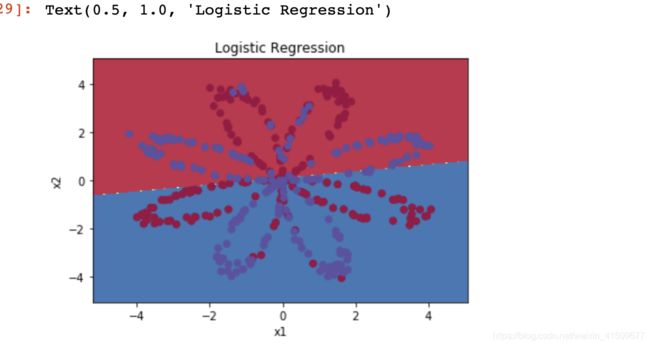
plot_decision_boundary(lambda x:model.predict(x), X, Y) #绘制决策边界
plt.title("Logistic Regression") #图标题

#predict函数要求（样本数目，特征数目）
lr_pre=model.predict(X.T)
lr_pre=lr_pre.reshape(400,1)
acc=np.mean(lr_pre==Y.T)
acc

0.47

准确性只有47%的原因是数据集不是线性可分的，所以逻辑回归表现不佳，所以我们选择构建神经网络。
构建的神经网络如图所示：

构建神经网络的一般方法是：

定义神经网络结构（输入单元的数量，隐藏单元的数量等）。
初始化模型的参数
循环：

• 实施前向传播
• 计算损失
• 实现反向传播
• 更新参数（梯度下降）

def initialize(n_x,n_h,n_y):
  np.random.seed(2) #指定一个随机种子，以便你的输出与我们的一样。
  W1 = np.random.randn(n_h,n_x) * 0.01
  b1 = np.zeros((n_h, 1))
  W2 = np.random.randn(n_y,n_h) * 0.01
  b2 = np.zeros((n_y, 1))    
  return W1,b1,W2,b2

实施前向传播

def forward_propagation(X,W1,b1,W2,b2):
  Z1 = np.dot(W1 , X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2 , A1) + b2
    A2 = sigmoid(Z2)
    cache = {
     'Z1': Z1,
             'A1': A1,
             'Z2': Z2,
             'A2': A2}
    return A2, cache

计算损失

def compute_cost(A2,Y):
  m = Y.shape[1]
    #计算成本
    logprobs =  np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
    cost = - np.sum(logprobs) / m 
    return cost

实现反向传播

def backward_propagation(W1,W2,cache,X,Y):
  m = X.shape[1]
    A1 = cache['A1']
    A2 = cache['A2']
    
    dZ2= A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
    grads = {
     'dW1': dW1,
             'db1': db1,
             'dW2': dW2,
             'db2': db2 }
    return grads

更新参数（梯度下降）

def update_param(W1,W2,b1,b2,grads,lr=0.5):
  dW1,dW2 = grads['dW1'],grads['dW2']
    db1,db2 = grads['db1'],grads['db2']
    
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2  
    return W1,b1,W2,b2

把上述函数放入模型中

def model(X,Y,n_h,iters,print_cost=False):
  np.random.seed(3)
  W1,b1,W2,b2=initialize(X.shape[0],n_h,Y.shape[0])
  for i in range(iters):
    A2, cache=forward_propagation(X,W1,b1,W2,b2)
    cost=compute_cost(A2,Y)
    grads=backward_propagation(W1,W2,cache,X,Y)
    W1,b1,W2,b2=update_param(W1,W2,b1,b2,grads,lr=0.5)
    if print_cost=True:
      if i%1000 == 0:
          print("第 ",i," 次循环，成本为："+str(cost))
  return W1,b1,W2,b2

W1,b1,W2,b2=nn_model(X,Y,n_h=4,num_iterations=10000,print_cost=True)

注意⚠️之前之所以会每一次循环后的cost都一样0.6930480201239823，是因为W1,b1,W2,b2 是每次循环都会变化的，每次循环都更新他们的值，之前可能没有对应，导致每次可能都是在算第一次的cost？

def predict(W1,b1,W2,b2,X):
    m=X.shape[1]
    y=np.zeros((1,m))
    A2 , cache = forward_propagation(X,W1,b1,W2,b2)
    for i in range(A2.shape[1]):
        if A2[0,i]<0.5:
            y[0,i]=0
        else:
            y[0,i]=1
    
    return y

#代入模型的x是(1038240,2)
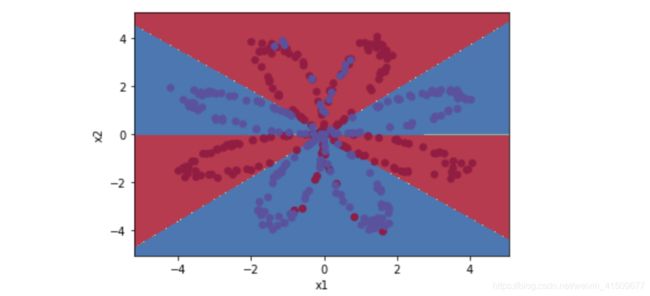
plot_decision_boundary(lambda x: predict(W1,b1,W2,b2, x.T), X, Y)
#如果没有用x.T会报下面的错
#ValueError: shapes (4,2) and (1038240,2) not aligned: 2 (dim 1) != 1038240 (dim 0)

计算准确率

y=predict(W1,b1,W2,b2,X)
acc=np.mean(y==Y)
acc

准确率是0.905

改变隐藏层的节点数目，观察对结果的影响

hidden_layer=[1,2,3,4,5,20,30]
plt.figure(figsize=(12,8))
for i,n_h in enumerate(hidden_layer):
  plt.subplot(4, 2, i+1) #4行2列，i+1是索引
  plt.title('Hidden Layer of size %d' % n_h)
  W1,b1,W2,b2=nn_model(X,Y,n_h=4,num_iterations=10000,print_cost=True)
  plot_decision_boundary(lambda x: predict(W1,b1,W2,b2, x.T), X, Y)
  y_pre=predict(W1,b1,W2,b2,X)
  acc=np.mean(y_pre==Y)
  print("隐藏节点数量是%d,准确率是%f" %(n_h,acc))
  

隐藏节点数量是1,准确率是0.672500
隐藏节点数量是2,准确率是0.665000
隐藏节点数量是3,准确率是0.892500
隐藏节点数量是4,准确率是0.900000
隐藏节点数量是5,准确率是0.897500
隐藏节点数量是20,准确率是0.900000
隐藏节点数量是30,准确率是0.900000

• 较大的模型（具有更多隐藏单元）能够更好地适应训练集，直到最终的最大模型过度拟合数据。
• 最好的隐藏层大小似乎在n_h = 5附近。实际上，这里的值似乎很适合数据，而且不会引起过度拟合。
• 我们还将在后面学习有关正则化的知识，它允许我们使用非常大的模型（如n_h = 50），而不会出现太多过度拟合。

改变数据集观察结果

noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
noisy_circles[0].shape
noisy_circles[1].shape

(200, 2)
(200,)

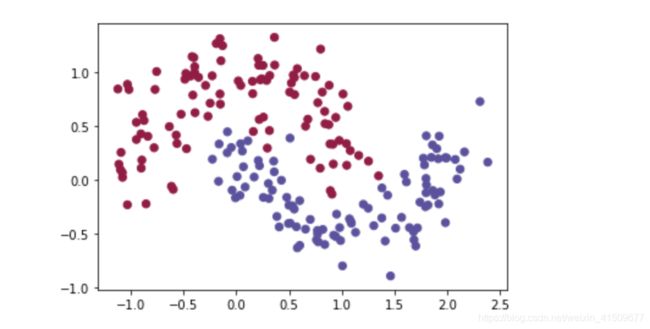
X1, Y1 = noisy_moons
X1，Y1=X1.T,Y1.reshape(1, Y1.shape[0])
plt.scatter(X1[0, :], X1[1, :], c=np.squeeze(Y1), s=40, cmap=plt.cm.Spectral)

params2 = nn_model(X1, Y1, n_h = 4, num_iterations=10000, print_cost=True)

第 0 次循环，成本为：0.692991456363002
第 1000 次循环，成本为：0.26474932422489267
第 2000 次循环，成本为：0.26292557997933425
第 3000 次循环，成本为：0.06839224486032959
第 4000 次循环，成本为：0.04394041585330925
第 5000 次循环，成本为：0.0387232225817003
第 6000 次循环，成本为：0.036205517821011377
第 7000 次循环，成本为：0.03466866202058001
第 8000 次循环，成本为：0.033581723226965454
第 9000 次循环，成本为：0.03272835124183427

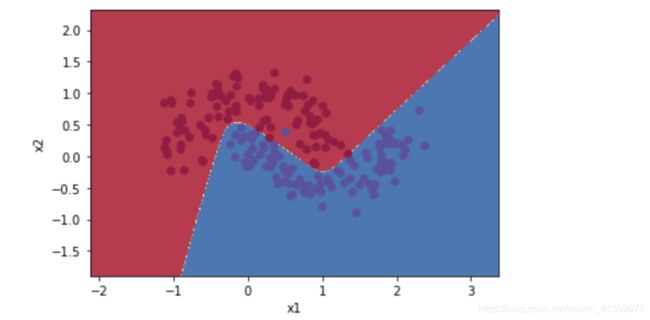
plot_decision_boundary(lambda x: predict(params2, x.T), X1, Y1)

y_pre1=predict(params2,X1)
acc=np.mean(y_pre1==Y1)
acc

准确率是0.995