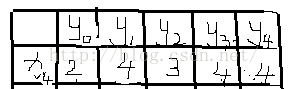KM算法（最优匹配）

最优匹配看了好多天，哎，就是因为一个细节问题没注意到，不知道网上的讲的不清还是本人智商不够，现在把我的误区说一下吧，顺便讲一下KM 算法，希望看KM算法的知识青年能少走弯路

KM算法是解决最优匹配问题的，关于最优匹配的相关术语网上说的很详细，可以先参考这个网站看下，http://philoscience.iteye.com/blog/1754498，本博客建立在此网站的基础上做的补充，是因为限于时间吧不能写的很详尽，希望对大家能有所帮助。

直入主题吧

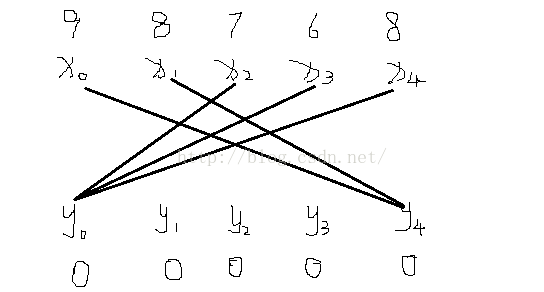
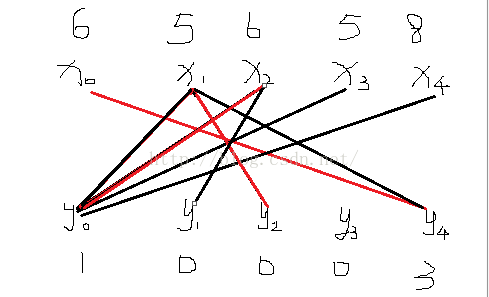
最优匹配：举个栗子，比如为每边输入n（n=5吧)个顶点，编号为(x0,x1,x2,x3,x4,,y0,y1,y2,y3,y4),首先为左侧顶点(即xi)寻找增广路

lx和ly的初始化

(0)为x0找增广路，即找到y4

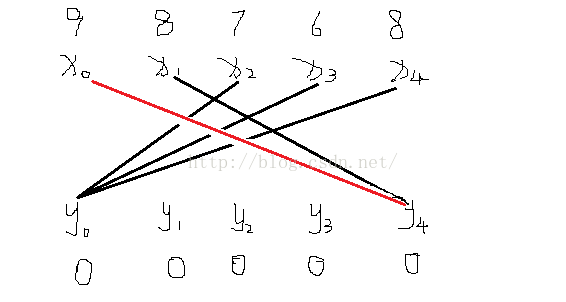
(1)为x1找增广路，即符合lx[cur]+ly[y]-g[cur][y]，例如即lx[x1]+ly[y4]-g[x1][y4]=0的条件，即寻增广路的路径为x1->y4->x0，x0没有路可寻，所以这形成了一棵交错树

即执行标杆的修改

即连接y0,x1

即这时的x1找到一条增广路x1->y0，修改后的匹配为

(2)为x2寻找增广路

同理因为lx[x2]+ly[y0]=7=map[x2][y0],即按照这个原理沿途寻增广路x2->y0->x1->y4->x0;

执行标杆的修改（即lx[i],ly[i])

即虽然x0,y2和x1,y2同值,但根据交错路,连接y2,x1

即连接后的路径为x2->y0->x1->y2,找的新的匹配边

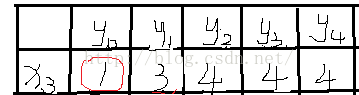
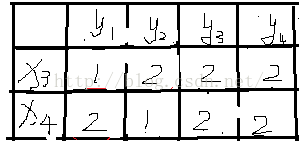
(3)为x3找边：因为lx[x3]+ly[y0]=7!=6=map[x3][y0],所以这棵交错树上就x3这一个顶点

找增广路失败，即把x3的标杆值lx[3]-1,既得图

再次寻找：x3->yo->x2,修改标杆的值为:

如图为

即找到新的增广路:x3->y0->x2->y1;

如图：

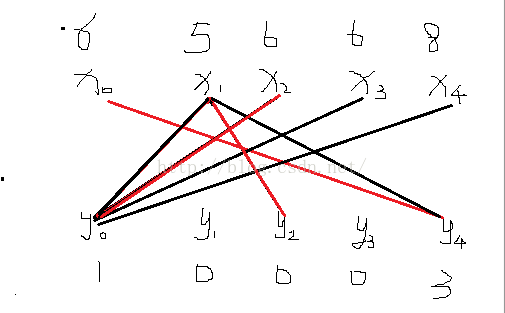
(4)为x4寻找择增广路,因为lx[x4]+ly[y0]=10!=map[x4][y0]=8,沿途x4,交错树中只有x4一个顶点，进行修改标杆操作：

如图：

继续为x4寻找增广路：因为lx[x4]+ly[y0]=8=map[x4][y0]，利用这个原理寻找x4的增广路:x4->y0->x3;

进行修改标杆：

即连接x3,y2:

匹配失败

限于时间，先匹配到这里吧；

最优匹配模板：

#include
#include
const int maxn=305;
const int INF=(1<<30)-1;
int g[maxn][maxn];
int lx[maxn],ly[maxn];
int match[maxn];
bool visx[maxn],visy[maxn];
int slack[maxn];
int n;
bool dfs(int cur)
{
	int y,t;
	visx[cur]=true;
	for(y=1;y<=n;y++)
	{
		if(visy[y])
		continue;
		t=lx[cur]+ly[y]-g[cur][y];
		if(t==0)
		{
			visy[y]=true;
			if(match[y]==-1||dfs(match[y]))
			{
				match[y]=cur;
				return true;
			}
		}
		else if(slack[y]>t)
			slack[y]=t;
	}
    return false;
}
int KM()
{
	int i,j,x;
	memset(match,-1,sizeof(match));
	memset(ly,0,sizeof(ly));
	for(i=1;i<=n;i++)
	{
		lx[i]=-INF;
		for(j=1;j<=n;j++)
			if(g[i][j]>lx[i])
			lx[i]=g[i][j];
	}//对ly[i]置0,对lx[i]取每行的最大值
	for(x=1;x<=n;x++)
	{
		for(i=1;i<=n;i++)
		slack[i]=INF;
		while(true)
		{
			memset(visx,false,sizeof(visx));
			memset(visy,false,sizeof(visy));
			if(dfs(x))
				break;
			int d=INF;
			for(i=1;i<=n;i++)
			{
				if(!visy[i]&&d>slack[i])
					d=slack[i];
			}
			for(i=1;i<=n;i++)
			{
				if(visx[i])
				lx[i]-=d;
			}
			for(i=1;i<=n;i++)
			{
				if(visy[i])
				ly[i]+=d;
				else
				slack[i]-=d;
			}
		}
	}
	int result=0;
	for(i=1;i<=n;i++)
		if(match[i]>-1)
		result+=g[match[i]][i];
	return result;
}
int main()
{
	int cost,i,j;
	while(scanf("%d",&n)!=EOF)
	{
		for(i=1;i<=n;i++)
		{
			for(j=1;j<=n;j++)
			{
				scanf("%d",&cost);
			    g[i][j]=cost;
			}
		}
		printf("%d\n",KM());
	}
	return 0;
}