AVL的插入,删除操作
在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
AVL树可以是空树,也可以是具有以下性质的树:
(1):他的左右子树都是AVL树
(2):左子树和右子树高度之差(平衡因子)的绝对值不超过1
特点:
AVL树本质上还是一棵二叉搜索树,它的特点是:
1.本身首先是一棵二叉搜索树。
2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
操作:
旋转
AVL树的基本操作一般涉及运做同在不平衡的二叉查找树所运做的同样的算法。但是要进行预先或随后做一次或多次所谓的”AVL 旋转”。
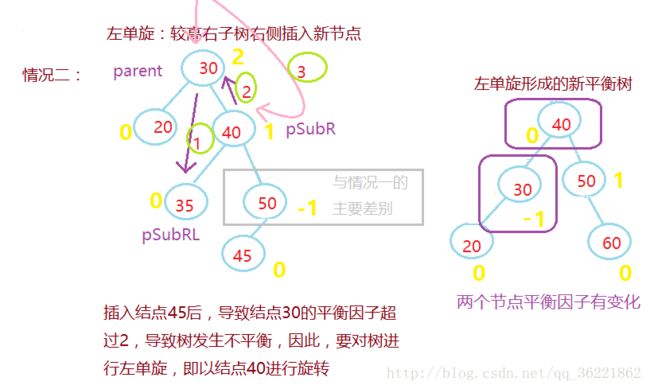
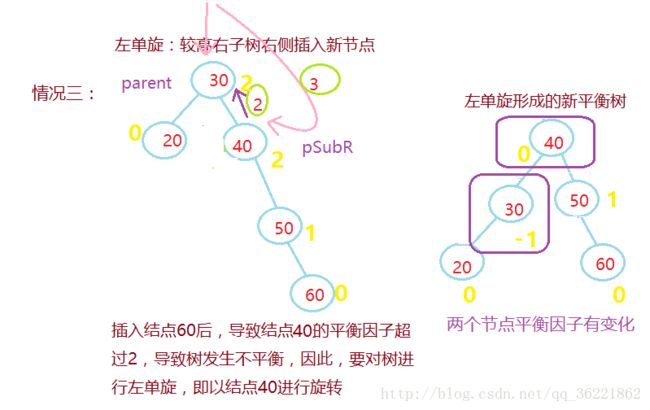
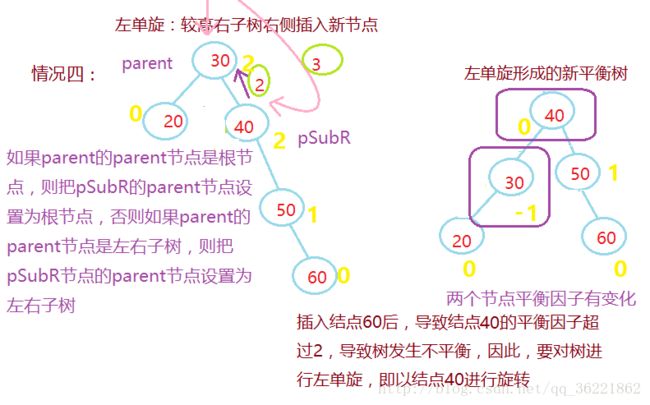
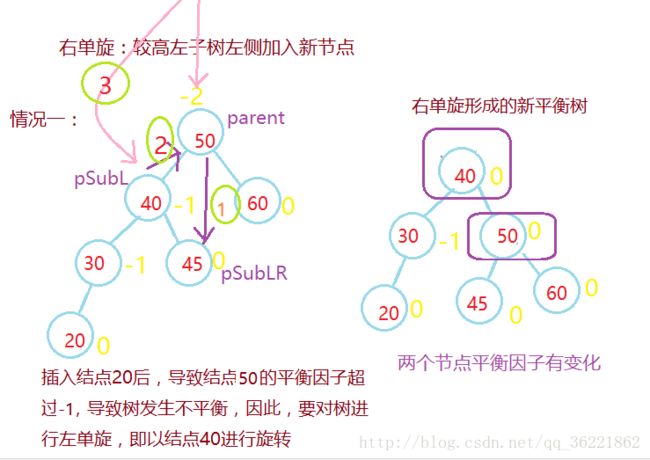
假设由于在二叉排序树上插入结点而失去平衡的最小子树根结点的指针为a(即a是离插入点最近,且平衡因子绝对值超过1的祖先结点),则失去平衡后进行进行的规律可归纳为下列四种情况:
单向左旋平衡处理R:由于在*a的右子树根结点的右子树上插入结点,*a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行一次左旋转操作;
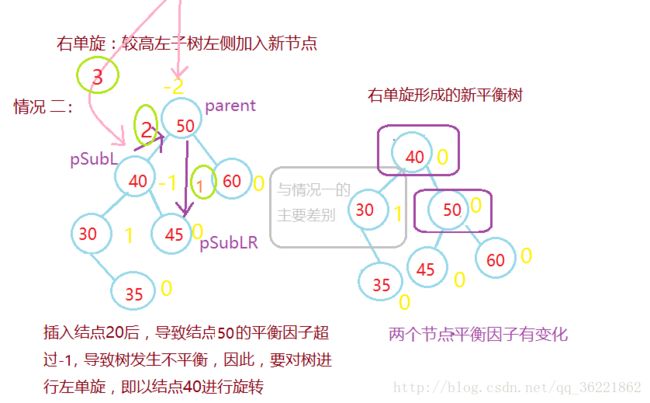
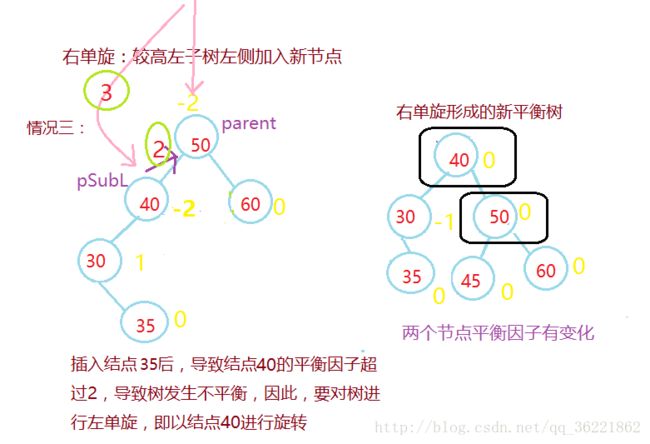
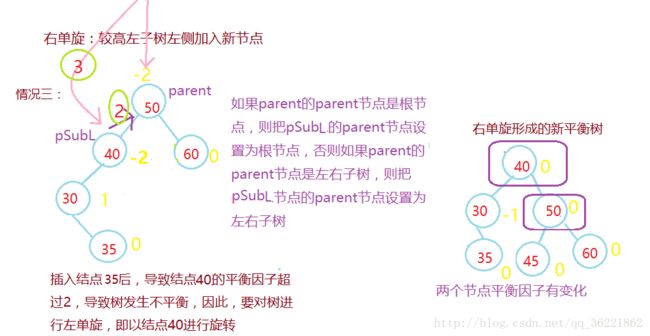
单向右旋平衡处理L:由于在*a的左子树根结点的左子树上插入结点,*a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行一次右旋转操作;
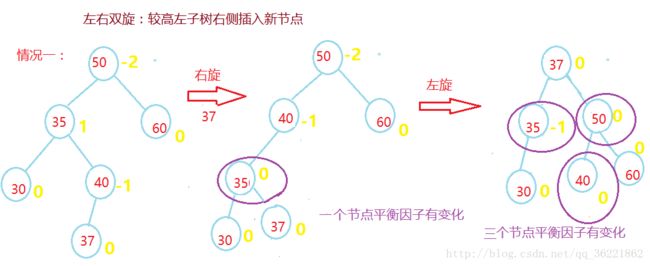
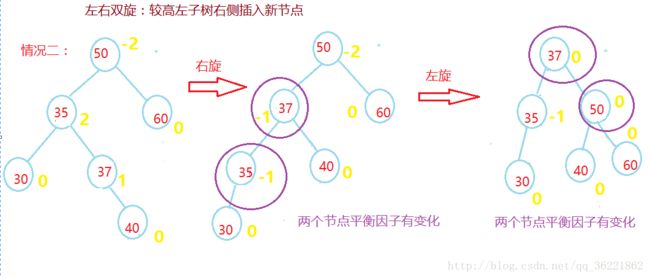
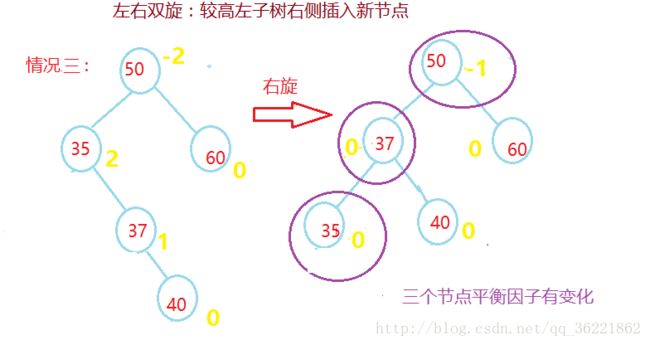
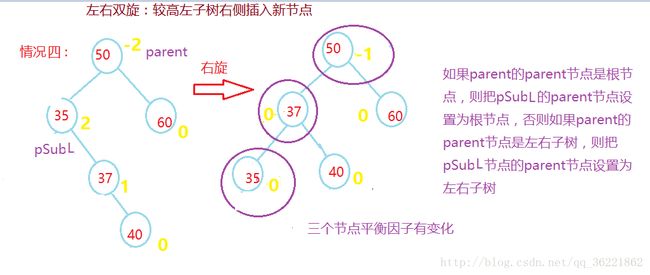
双向旋转(先左后右)平衡处理LR:由于在*a的左子树根结点的右子树上插入结点,*a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行两次旋转(先左旋后右旋)操作。
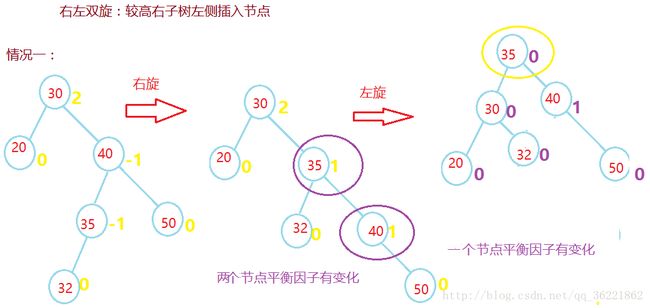
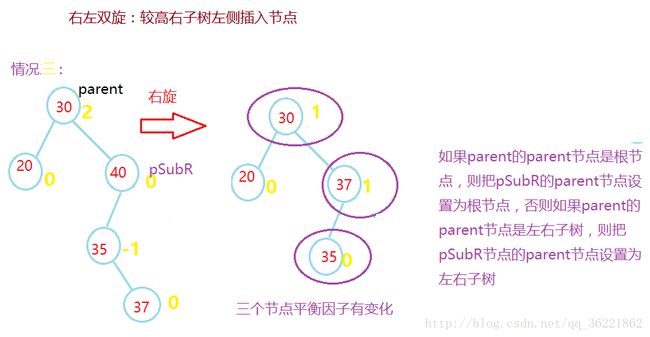
双向旋转(先右后左)平衡处理RL:由于在*a的右子树根结点的左子树上插入结点,*a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行两次旋转(先右旋后左旋)操作
插入
在向一棵本来高度平衡的AVL树中插入一个新节点时,如果树中某个结点的平衡因子的绝对 值>1,则出现了不平衡。设新插入结点为P,从结点P到根节点的路径上,每个结点为根的子 树的高度都可能增加1,因此在每执行一次二叉搜索树的插入运算后,都需从新插入的结点 P开始,沿该结点插入的路径向根节点方向回溯,修改各结点的平衡因子,调整整棵树的高 度,恢复被破坏的平衡性质。
在AVL树中插入结点P(key)结点算法:
步骤一:如果是空树,插入后即为根节点,插入后直接返回
步骤二:如果树不空,寻找插入位置,若在寻找的过程中找到key,则插入失败直接返回
步骤三:插入结点
步骤四:更新平衡因子,对树进行调整
新节点P的平衡因子为0,但其双亲结点Pr的平衡因子有三种情况:
1、结点Pr的平衡因子为0 在Pr的较矮的子树上插入新节点,结点Pr平衡,其高度没有增加,此时从Pr到根路径
上各结点为根的子树的高度不变,即各结点的平衡因子不变,结束平衡化处理。
2、结点Pr的平衡因子的绝对值为1; 插入前Pr的平衡因子为0,插入后以Pr为根的子树没有失去平衡,但该子树的高度增
加,需从该结点Pr向根节点方向回溯,继续查看Pr的双亲结点的平衡性。3、结点Pr的平衡因子的绝对值为2
新节点在较高的子树插入,需要做平衡化处理:
若Pr =2,说明右子树高,设Pr的右子树为q
当q的平衡因子为1,执行左单旋转
当q的平衡因子为-1,执行先右后左双旋转
若Pr = -2,说明左子树高,设Pr的左子树为q
当q的平衡因子为-1,执行右单旋转
当q的平衡因子为1,执行先左后右双旋转
旋转后Pr为根的子树高度降低,无需继续向上层回溯
*
删除:
从AVL树中删除一个节点,首先必须检测该结点是否存在,若存在删除该结点之后可能会破 坏AVL树的高度平衡,因此需要做平衡化旋转。
被删除的结点P存在以下情况:
1、被删除的结点P有两个孩子
首先搜索P在中序遍历中的直接前驱q(或直接后继)。再把结点q的内容传送给P,问题由删除节点P转移到删除节点q,它是只有一个孩子的结点。2、被删除的结点P最多只有一个孩子q
把P的双亲结点Pr中原来指向P的指针该指向q;如果P没有孩子,直接将Pr的相应指针 置为NULL。然后将原来以Pr为根的子树的高度减1,并沿Pr通向根的路径反向追踪高度的变化对路径上的各个结点的影响。
考查结点q的双亲结点P,若q是Pr的左孩子,则Pr的平衡因子增加1,否则减少1,根据修改后的 Pr的平衡因子值,分三种情况处理:
1、Pr平衡因子原来为0,在其左(或右)子树删除结点后,它的平衡因子增加(减少)1,Pr高度不变,因此从Pr到根所有节点高度均不变,不用调整。
2、Pr原来的平衡因子不为0,且较高的子树被缩短,Pr的平衡因子变成0,此时Pr为根的子 树平衡,其高度减1,但需要检查Pr的双亲结点的平衡性。
3、结点Pr的平衡因子不为0,且交矮子树被缩短,则Pr发生不平衡,需要进行平衡化旋转令使其平衡。令Pr较高子树的根为q,根据q的平衡因子,分一下三种情况
a、如果q的平衡因子为0,执行单旋转恢复Pr
b、如果q的平衡因子与Pr平衡因子(正负)号相同,则执行一个单旋转恢复Pr
c、如果q的平衡因子与Pr平衡因子(正负)号相反,则执行一个双旋转恢复Pr
代码实现:
#include<iostream>
using namespace std;
template<class K,class V>
struct AVLtreeNode //结点结构体
{
typedef AVLtreeNode<K, V> Node;
Node* _pLeft;
Node* _pRight;
Node* _pParent;
K _key;
V _value;
int _bf;
AVLtreeNode(const K& key,const V& value)
:_key(key)
, _value(value)
, _pLeft(NULL)
, _pRight(NULL)
, _pParent(NULL)
, _bf(0) //平衡因子
{}
};
template<class K,class V>
class AVLtree
{
typedef AVLtreeNode<K, V> Node;
public:
AVLtree()
:_pRoot(NULL)
{}
bool Insert(const K& key, const V& value)
{
//判断树是否存在
if (NULL == _pRoot)
{
_pRoot = new Node(key, value);
return true;
}
//找插入位置
Node* cur = _pRoot;
Node* parent = NULL;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_pRight;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_pLeft;
}
else
{
return false;
}
}
//插入新节点,双亲一定平衡,但双亲的双亲不一定平衡,
if (parent->_key < key)
{
Node* tmp = new Node(key, value);
parent->_pRight = tmp;
tmp->_pParent = parent;
parent->_bf++;
}
if (parent->_key>key)
{
Node* tmp = new Node(key, value);
parent->_pLeft = tmp;
tmp->_pParent = parent;
parent->_bf--;
}
//更新双亲的平衡因子
while (parent)
{
if (parent->_bf == 0) //原来是1或者-1,那插入以后不会对树的高度有影响;
{
return true;
}
else if (parent->_bf == 1 || parent->_bf == -1) //原来是0,对树的高度有影响
{
Node* pparent = parent->_pParent;
if (pparent != NULL)
{
if (pparent->_pLeft == parent)// 左树上高度增加
pparent->_bf--;
else //右树上高度增加
pparent->_bf++;
}
parent = pparent;
}
else //平衡因子是2/-2,从1或者-1变过来,不满足平衡树,需要旋转
{
if (parent->_bf == 2) //右树过高
{
if (parent->_pRight->_bf == 1) //需要左旋结构
{
_RotateL(parent);
return true;
}
else if (parent->_pRight->_bf = -1) //需要右左旋结构
{
_RotateRL(parent);
return true;
}
}
else //平衡因子为-2
{
if (parent->_pLeft->_bf == -1) //需要右单旋的结构
{
_RotateR(parent);
return true;
}
else if (parent->_pLeft->_bf == 1) //需要左右旋的结构
{
_RotateLR(parent);
return true;
}
}
}
}
}
bool Remove(const K& key, const V& value)
{
//二叉搜索树中没有节点
if(_pRoot == NULL)
return false;
//二叉搜索树中只有根节点
if(_pRoot->_pLeft == NULL && _pRoot->_pRight == NULL)
{
if(_pRoot->_key == key)
{
delete _pRoot;
_pRoot = NULL;
return true;
}
return false;
}
Node* pCur = _pRoot;
Node* parent = NULL;
//遍历查找要删除节点的位置
while(pCur)
{
Node* pDel = NULL;
if(pCur->_key < key)
{
parent = pCur;
pCur = pCur->_pRight;
}
else if(pCur->_key > key)
{
parent = pCur;
pCur = pCur->_pLeft;
}
else
{
//要删除节点的左子树为空
if(pCur->_pLeft == NULL)
{
//判断父节点是否为空,若为空,则要删除的节点为根节点
if (parent == NULL)
{
_pRoot = pCur->_pRight;
delete pCur;
pCur = NULL;
return true;
}
else if(parent->_key < key) //右子树
{
pDel = pCur;
parent->_pRight = pCur->_pRight;
delete pDel;
pDel = NULL;
return true;
}
else //左子树
{
pDel = pCur;
parent->_pLeft = pCur->_pRight;
delete pDel;
pDel = NULL;
return true;
}
}
//要删除节点的右子树为空
else if(pCur->_pRight == NULL)
{
//判断父节点是否为空,若为空,则要删除的节点为根节点
if (parent == NULL)
{
_pRoot = pCur->_pLeft;
delete pCur;
pCur = NULL;
return true;
}
else if(parent->_key > key) //左子树
{
pDel = pCur;
parent->_pLeft = pCur->_pLeft;
delete pCur;
pCur = NULL;
return true;
}
else //右子树
{
pDel = pCur;
parent->_pRight = pCur->_pLeft;
delete pDel;
pDel = NULL;
return true;
}
}
//左右子树都不为空
//右子树中序遍历第一个节点,用它的值替换被删除节点的值,在进行删除
else
{
Node* pDel = pCur;
Node* parent = NULL;
Node* RightFirst = pCur->_pRight;
//右边第一个节点的左子树为空
if (RightFirst->_pLeft == NULL)
{
swap(RightFirst->_key, pCur->_key);
swap(RightFirst->_value, pCur->_value);
//交换删除节点与中序遍历第一个节点的值,即就是最左边节点
pDel = RightFirst;
pCur->_pRight = RightFirst->_pRight;
delete pDel;
return true;
}
//右边第一个节点的左子树不为空
while (RightFirst->_pLeft)
{
parent = RightFirst;
RightFirst = RightFirst->_pLeft;
}
swap(RightFirst->_key, pCur->_key);
swap(RightFirst->_value, pCur->_value);
pDel = RightFirst;
parent->_pLeft = RightFirst->_pRight;
delete pDel;
return true;
}
}
}
//更新平衡因子
while(parent)
{
//更新平衡因子
if(parent->_pLeft == pCur)
(parent->_bf)--;
else
(parent->_bf)++;
if(parent->_bf == parent->_bf == -1 || parent->_bf == 1)//parent是叶子节点,插入节点后其平衡因子可能是1或-1
return true; //此时树的高度没有发生变化,该树任然是是AVL树
else if(parent->_bf == 0)//parent只有左孩子或者只有右孩子,在其空指针域插入一个节点后,平衡因子为0,
{ //此时树的高度可能发生了改变,我们要向上判断其祖先节点是否平衡
pCur = parent;
parent = pCur->_pParent;
}
else
{
//不满足平衡树,要做旋转处理
if(parent->_bf == 2)//右子树
{
if(pCur->_bf == 1)//右侧
_RotateL(parent);//左旋调整
else//左侧
_RotateRL(parent);//先右旋再左旋
}
else//左子树
{
if(pCur->_bf == -1)//左侧
_RotateR(parent);
else//右侧
_RotateLR(parent);
}
}
}
return true;
}
bool IsBalance()
{
return _IsBalance(_pRoot);
}
void InOrder()
{
_InOrder(_pRoot);
cout << endl;
}
protected:
bool _IsBalance(Node* root)
{
if (NULL == root)
return true;
int bf = _Height(root->_pRight) - _Height(root->_pLeft);
if (bf == root->_bf)
return true;
else
{
cout << root->_key << "平衡因子异常" << endl;
return false;
}
return _IsBalance(root->_pLeft) && _IsBalance(root->_pRight);
}
int _Height(Node* root)
{
if (NULL == root)
return 0;
int left = _Height(root->_pLeft)+1;
int right = _Height(root->_pRight) + 1;
return left > right ? left : right;
}
void _InOrder(Node* root)
{
if (NULL == root)
return;
_InOrder(root->_pLeft);
cout << root->_key << " ";
_InOrder(root->_pRight);
}
void _RotateL(Node* parent) //左单旋
{
Node* subR = parent->_pRight;
Node* subRL = subR->_pLeft;
parent->_pRight = subRL;
if (subRL)
subRL->_pParent = parent;
Node* pparent = parent->_pParent;
subR->_pLeft = parent;
parent->_pParent = subR;
if (NULL == pparent)
{
_pRoot = subR;
subR->_pParent = NULL;
}
else
{
if (pparent->_pLeft == parent)
{
pparent->_pLeft = subR;
subR->_pParent = pparent;
}
else
{
pparent->_pRight = subR;
subR->_pParent = pparent;
}
}
parent->_bf = subR->_bf = 0;
}
void _RotateR(Node* parent) //右单旋
{
Node* subL = parent->_pLeft;
Node* subLR = subL->_pRight;
parent->_pLeft; = subLR;
if (subLR)
subLR->_pParent = parent;
Node* pparent = parent->_pParent;
subL->_pRight = parent;
parent->_pParent = subL;
if (pparent == NULL)
{
_pRoot = subL;
subL->_pParent = NULL;
}
else
{
if (pparent->_pLeft == parent)
{
pparent->_pLeft = subL;
subL->_pParent = pparent;
}
else
{
pparent->_pRight = subL;
subL->_pParent = pparent;
}
}
parent->_bf = subL->_bf = 0;
}
void _RotateRL(Node* parent) //右左双旋
{
Node* subR = parent->_pRight;
Node* subRL = subR->_pLeft;
int bf = subRL->_bf; //必须记录下来,旋转后发生改变
_RotateR(subR);
_RotateL(parent);
if (bf == 1) //插入后右树高,右树给了subR的左边,所以subR的平衡因子为0,左树高度低于右树,给了parent的右树所以parent的平衡因子为1
parent->_bf = -1;
else if (bf == -1)//插入后左树高,右树给了subR的左边,所以subR的平衡因子为1,左树高度低于右树,给了parent的右树所以parent的平衡因子为0
subR->_bf = 1;
}
void _RotateLR(Node* parent) //左右双旋
{
Node* subL = parent->_pLeft;
Node* subLR = subL->_pRight;
int bf = subLR->_bf;
_RotateL(subL);
_RotateR(parent);
if (bf == 1)
{
subL->_bf = -1;
}
else if(bf == -1)
{
parent->_bf = 1;
}
}
private:
Node* _pRoot;
};
void TestAVLtree()
{
AVLtree<int, int> tree;
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
for (size_t i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
tree.Insert(a[i], a[i]);
}
tree.InOrder();
if(tree.IsBalance())
cout<<"AVL是平衡树"< tree1;
int a1 [] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
for (size_t i = 0; i < sizeof(a1) / sizeof(a1[0]); i++)
{
tree1.Insert(a1[i], i);
}
tree1.InOrder();
if(tree1.IsBalance())
cout<<"AVL是平衡树"<