算法-23-单词查找树（字符串搜索最快算法）

目录

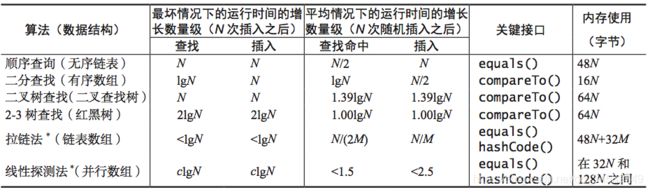
1、各种字符串查找算法性能比较

2、定义

3、查找

4、插入

5、结点详解

6、单词查找树数据结构代码

7、查找所有的键

8、删除

9、单词查找树的性质

10、三向单词查找树

11、三向单词查找树的性质

12、各种字符串查找算法的性能特点

---

1、各种字符串查找算法性能比较

假设这里有N个名字，我们需要找到自己的名字的话，并得到自己的分数的话，最简单的方法是遍历这N个字符串，直到找到自己的名字，但是我们也可以用下图中的算法来缩短我们查找的时间。

算法-13-符号表（HashMap的前世一）

算法-14-二叉查找树（HashMap的前世二）

算法-15-平衡查找树

算法-16-红黑树

算法-17-散列表（拉链法+线性探测法）

如图中可以看到我们从N个名字，找到自己的名字，平均情况下，我们需要lgN的时间复杂度，虽然这已经很优秀了，但是还有没有更短的时间呢？那就是本节我们将要讲的单词查找树，就比如我的名字叫Zhang San，我们只需要查找8次就可以找到我的自己，这对于成千上万的数据来说，这样的查找速度是非常诱人的。

2、定义

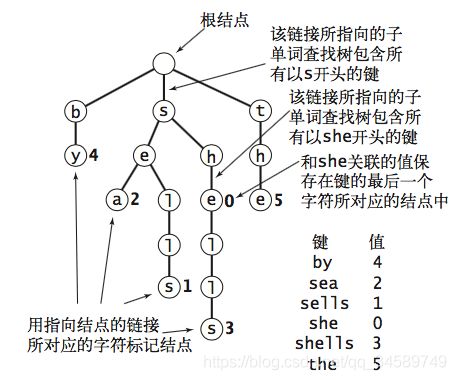
我们的单词查找树其实就是根据字符串中的字符数组构造成一棵树，一个字符串就是一个树枝zhang---->z-h-a-n-g，也有可能多个字符串共享一个树枝zhan和zhang共享一个树枝，当我们查找指定字符串的时候，从首字母字符出发，不断地按照查找字符串中字符的顺序来查找，直到这条路径存在并且返回相应的值为止。

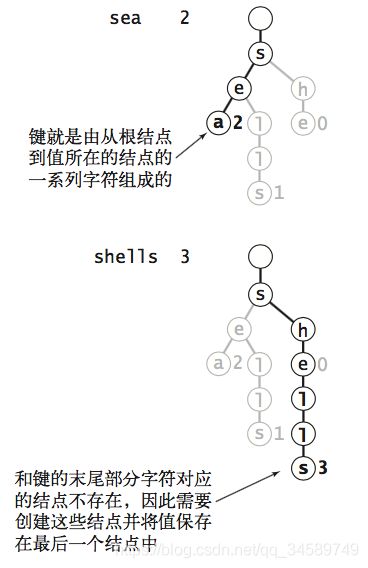
就比如我们有by、sea、sells、she、shells、the  六个字符串，我们构造的查找树如下：

树的每条路径都是以链表的形式连接起来的。

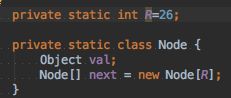
每个结点的代码如右上图，每个结点都保存了值（分数）和一个26大小的Node数组，为啥是26呢？假设我们的字符串只能是26个英文字母，那么该结点后面可能跟着的是这26字母中的其中一个，所以我们需要创建一个字母表大小的数组来存储。（通俗点说就是我们的字符串可能是ab、aa、ac、af、ag----a后面可能跟着26个字母其中的一个）

3、查找

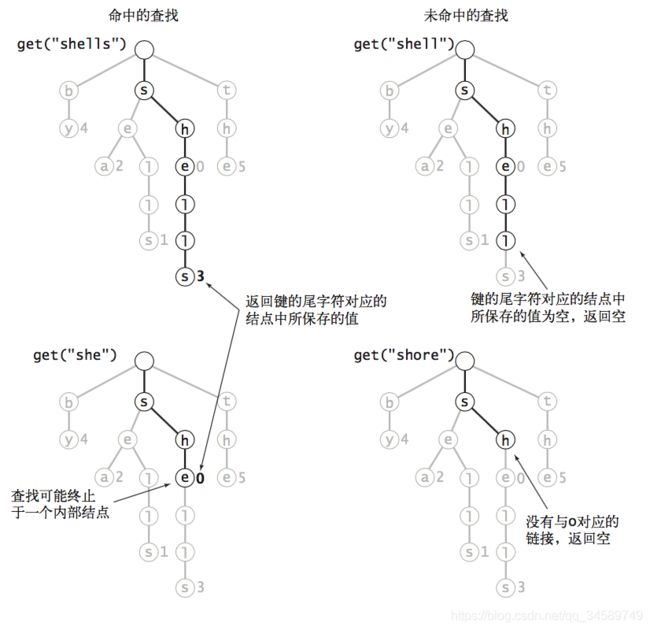
从上面的结点代码可以看到，每个结点都保存一个Object的值，这个值就代表了我们要找的字符串是否存在于我们的单词查找树中。

从下面的图中可以看到我们查找命中和不命中都有两种情况，当我们查找一个字符串shells的时候，我们会从根结点的26数组中找到s 开头的树枝，然后我们从s 结点的26数组中，找到h开头的树枝，然后在从h 结点的26数组中找到 e开头的树枝，这样不断向下找，当我们走过的树枝长度等于 shells 字符串的长度时，然后判断最后一个字符 s 结点的 Object 值 是否为null，如果是null的话说明我们这个树中没有该字符串，不为null就说明 有这个字符串。

4、插入

插入操作会遇到两种情况，当我们沿着插入的字符串中字符的顺序的树枝走的时候，如果遇到了空结点，那么说明我们这棵树中还没有对应的字符，这时候我们需要在这个树枝后面不断创建新的结点，直到所有的字符都添加到树中为止。第二种情况就是我们在遇到空结点之前我们就走到了这个字符串的最后一个字符，这时候我们就需要看看原树枝中该结点是否有值，有值就替换，没值就添加（因为我们该树不允许有重复的键存在）。

下图是插入sea、shells字符串的图解。

5、结点详解

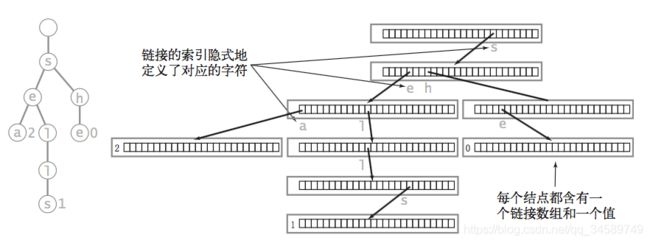
从上面的结点代码可以看到，我们每个结点都会保存你可能使用的字母数量大小的数组，数组中每个元素都保存着对下一个字符结点的引用。因为我们使用的String字符串，其实它的取值大小为0-255，也就是256个字符。

字符串字符的代码范围为 0–255。 字符集的前128个字符–(0 127) 对应于标准美国键盘上的字母和符号。 这些前 128 个字符与 ASCII 字符集定义的字符相同。 第二个128个字符–(128 255) 表示特殊字符, 如国际字母表中的字母、重音、货币符号和分数。

所以我们每个结点中将会保存一个256大小的数组，还有一个Object值用来保存我们的键值对。

其实我们这棵树中没有保存任何字符串信息，属于隐式地保存在这棵树中，就比如san这个字符串，我们的char其实可以作为int类型，而我们String中的每个字符的取值是0-255。所以存储san这个字符串 我们会从根结点的数组中找到s开头的树枝---next[s]，然后从s结点的数组中找到a开头的结点 next[a] 。

• 每个结点都含有 R 个链接，对应着每个可能出现的字符;
• 字符和键均隐式地保存在数据结构中。

数据结构既没有保存字符串 sea 也没有保存字符 s、e 和 a。事实上，数据结构不会存储任 何字符串或字符，它保存了链接数组和值。因为参数 R 的作用的重要性，所以将基于含有 R 个字符 的字母表的单词查找树称为 R 向单词查找树。

6、单词查找树数据结构代码

下面的代码只书写的插入和查找的代码。

public class TrieST {

    private static int R=256; //字符串中有256个字符，取值为0到255
    private static Node root;
    private static class Node {
        Object val;
        Node[] next = new Node[R];
    }
    /**
     * 插入字符串
     */
    public void put(String key,Value val) {
        root=put(root,key,val,0);
    }
    /**
     *
     * @param x   当前字符所在的结点
     * @param key 插入的字符串
     * @param val 插入的字符串对应的值
     * @param d   走到了该字符串的第几个字符
     * @return    返回当前结点的引用，给前一个字符所在的结点，这样就能保持按照字符顺序形成链接
     */
    private Node put(Node x,String key,Value val,int d) {

        if (x==null) x= new Node();                     //1、如果沿着插入字符串的树枝走的时候，发现树枝后面没有该字符就给该树枝添加新的结点
        if (d==key.length())  { x.val=val; return x; }  //2、如果走到了尾字符所在的结点，更新对应的值

        char n=key.charAt(d);                           //3、获取当前结点保存的对下一个结点的引用
        x.next[n]= put(x.next[n],key,val,d+1);       //4、走向树枝下一个结点，并更新对下一个结点的引用
        return x;
    }

    /**
     * 获取字符串key对应值
     */
    public Value get(String key) {
        Node x = get(root, key, 0);
        if (x==null) return null;
        return (Value) x.val;
    }

    public Node get(Node x, String key, int d){
        if (x==null) return null;                   //1、如果没有该分支就返回null
        if (d==key.length()) return x;              //2、如果走到了与key字符串长度相等的位置，返回当前结点，至于是否有val值在上面的get判断

        char n=key.charAt(d);                       //3、获取当前结点保存的对下一个结点的引用
        return get(x.next[n],key,d+1);          //4、走向树枝下一个结点，并返回最后一个结点的结果
    }
}

7、查找所有的键

从上面的介绍我们知道，我们整棵单词查找树中其实是没有保存字符串的信息的，当我们想要获取所有字符串信息的时候，我们就需要遍历我们查找树来获取所有字符串信息。

这里我们先介绍一个获取以某个字符串为前缀的所有字符串的函数keysWithPrefix() 。比如she、shells、hello、by 四个字符串中以sh为前缀的字符串有she、shells。那这个函数的思想就是获取到sh h字符所在的结点，然后遍历从这个结点出发的所有树枝，然后判断它们的值，不为null就说明有字符串存在，然后加入到队列中，最后返回该队列。

获取单词查找树中所有的字符串。这里通过获取前缀字符串的方法来获取所有字符串，当以空字符串为前缀的时候，得到的是根结点，这样遍历根结点就获取所有字符串了。

   /**
     * 获取单词查找树中所有的字符串。
     * 这里通过获取前缀字符串的方法来获取所有字符串，当以空字符串为前缀的时候，
     * 得到的是根结点，这样遍历根结点就获取所有字符串了。
     */
    public Iterable keys() {
        return keysWithPrefix("");
    }

    /**
     * 获取所有以pre字符串为前缀的字符串，
     * she、shells、hello、by 以sh为前缀的字符串有she、shells
     */
    public Iterable keysWithPrefix(String pre) {

        Queue queue=new Queue<>();
        Node start=get(root,pre,0);   //获取到前缀字符串 sh h所在的结点。

        collect(start,pre,queue);
        return queue;
    }

    private void collect(Node x, String pre, Queue queue) {

        if (x==null) return;                      //1、如果遇到空结点，就返回
        if (x.val!=null) queue.enqueue(pre);      //2、如果该结点的值不为空，那么该字符串存在加入到队列中 

        for (char c = 0; c < R; c++) {            //3、遍历该结点的所有可能存在的下一个结点，重复上面的1、2步将所有以pre 为前缀的字符串加入到队列中
            collect(x.next[c],pre+c,queue);  
        }
    }

8、删除

 /**
     * 删除指定的String 键
     */
    public void delete(String key) {
        root=delete(root,key,0);
    }

    /**
     * 删除指定String字符串 会有两种情况：
     * 一种是该字符串树枝后面还有其他字符串，这样将该结点的val值置空就可以了
     * 第二种是删除的字符串单独占着一个树枝，这样就需要将这个树枝上所有的字符结点置空
     * @param x    查询到当前结点
     * @param key  删除的字符串
     * @param d    走到key的第一个字符
     * @return     将本结点的信息返回给上一个结点。
     */
    private Node delete(Node x, String key, int d) {

        if (x==null)return  null;
        if (d == key.length()) {
            x.val=null;
        }else {
            char c=key.charAt(d);
            x.next[c] = delete(x.next[c], key, d + 1);
        }

        if (x.val!=null) return x;

        for (char c = 0; c < R; c++) {
            if (x.next[c].val!=null) return x;
        }
        return null;
    }

9、单词查找树的性质

1、单词查找树的链表结构(形状)和键的插入或删除顺序无关:对于任意给定的一组键， 其单词查找树都是唯一的。

2、在单词查找树中查找一个键或是插入一个键时，访问数组的次数最多为键的长度加 1。

3、字母表的大小为 R，在一棵由 N 个随机键构造的单词查找树中，未命中查找平均所需 检查的结点数量为 ~logRN。

4、一棵单词查找树中的链接总数在 RN 到 RNw 之间，其中 w 为键的平均长度。当所有键均较短时，链接的总数接近于 RN;当所有键均较长时，链接的总数接近于 RNw;因此缩小R能够节省很大的空间。

10、三向单词查找树

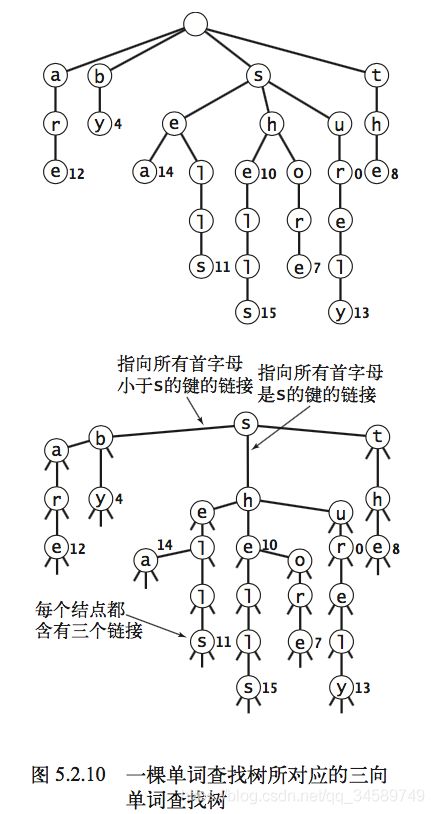
为了避免 R 向单词查找树过度的空间消耗，我们现在来学习另一种数据的表示方法:三向单词查 找树(TST)。在三向单词查找树中，每个结点都含有一个字符、三条链接和一个值。这三条链接分 别对应着当前字母小于、等于和大于结点字母的所有键。

在 R 向单词查找树中，树的结点 含有 R 条链接，每个非空链接的索引隐式地表示了它所对应的字符。在等价的三向单词查找树中，字 符是显式地保存在结点中的——只有在沿着中间链接前进时才会根据字符找到表中的键。

public class TST {

    private Node root;

    private class Node {
        char c;
        Value val;
        Node left, mid, right;
    }

    /**
     * 插入某个键值对
     */
    public void put(String key, Value val) {
        root = put(root, key, val, 0);
    }

    private Node put(Node x, String key, Value val, int d) {

        if (x == null) {                                   //如果该分支没有后序字符，创建新的结点分支
            x = new Node();       
            x.val = val;
        }
        char c = key.charAt(d);                            // 走到哪个字符了，并那该字符和结点中的值表，小于去左侧分支，大于去右侧分支找
        if (c < x.c) {
            x.left = put(x.left, key, val, d);
        } else if (c > x.c) {
            x.right = put(x.right, key, val, d);
        } else if (d < key.length() - 1) {                 //等于的话，如果没走到该字符的最后一个字符，还得继续往下找
            x.mid = put(x.mid, key, val, d + 1);
        } else {
            x.val = val;
        }
        return x;
    }

    public Value get(String key) {

        Node x = get(root, key, 0);
        if (x == null)
            return null;
        return x.val;
    }

    private Node get(Node x, String key, int d) {

        if (x == null)
            return null;

        char c = key.charAt(d);
        if (c < x.c) {
            return get(x.left, key, d);
        } else if (c > x.c) {
            return get(x.right, key, d);
        } else if (d < key.length() - 1) {
            return get(x.mid, key, d + 1);
        }
        return x;
    }
}

11、三向单词查找树的性质

1、和其他所有二叉查找树一样，每个三向单词查找树结点的二叉查找树表示也取决于键的插入顺序。

2、三向单词查找树最重要的性质就是每个结点只含有三个链接，因此三向单词查找树所需要空间 远小于对应的单词查找树。

3、由 N 个平均长度为 w 的字符串构造的三向单词查找树中的链接总数在 3N 到 3Nw 之间。

4、在一棵由 N 个随机字符串构造的三向单词查找树中，查找未命中平均需要比较字符~ lnN 次。除~ lnN 一次插入或命中的查找会比较一次被查找的键中的每个字符。

5、使用三向单词查找树的最大好处是它能够很好地适应实际应用中可能出现的被查找键的不规则性。有了三向单词查找树，我们可以使用 256 个字符的 ASCII 编码或者 65 536 个字符的Unicode编码，而不必担心256向分支或者65 536向分支带来的巨大开销，也不必判断哪 些才是相关的字符集。

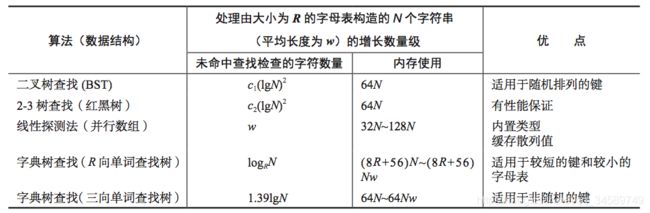
12、各种字符串查找算法的性能特点