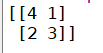不平衡数据的处理

参考博文数据不平衡与smote算法
smote算法，python实现

我当时看到这个问题，首先思考：何为不平衡数据？不平衡数据是如何产生的？

1. 何为不平衡数据？

可通过一些具体例子来理解

例如在信贷评估中，违约的是少数、医学影响的癌细胞识别中，癌细胞是少数、公用事业欺诈检测，欺诈的是少数等

2. 不平衡数据不经过处理，直接建模会产生什么影响？

为了解决这个问题，我们首先要了解混淆矩阵，AUC值和ROC曲线

2.1 混淆矩阵

混淆矩阵也称为误差矩阵，是表示精度评估的一种标准格式，用n行n列的矩阵形式表示。具体评估指标有准确率、精确率和召回率等。在人工智能领域，混淆矩阵作为一种可视化工具被广泛使用

• TP(True Positive): 真实为0，预测也为0
• FN(False Negative): 真实为0，预测为1
• FP(False Positive): 真实为1，预测为0
• TN(True Negative): 真实为0，预测也为0

举个例子，直观了解一下
假设我们有一个两类分类问题：根据照片内判断男女，以下是一个包含10个记录的测试数据集，包含标签分类和模型的预测结果

标签分类	预测结果
男	女
男	男
女	女
男	男
女	男
女	女
女	女
男	男
男	女
女	女

设1-男，0-女，则混淆矩阵如下：

真实情况	预测结果
	1	0
1	3（TP）	2（FN）
0	1（FP）	4（TN）

1. 准确率（Accuracy）

（1）什么是准确率？

所有预测正确的样本占所有样本的比例

（2）计算公式

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
在例子中，$Accuracy=\frac{7}{10}$

2. 精确率 （Precision）

（1）什么是精确率？

预测结果为正例的样本中真实为正例的比例

（2）计算公式

$$Precision=\frac{TP}{TP+FP}$$

在例子中，$Precision=\frac{3}{4}$

3. 召回率（Recall）/灵敏度

（1）什么是召回率？

实为正例的样本中预测结果为正例的比例

（2）计算公式

$$Recall=\frac{TP}{TP+FN}$$
在例子中，$Recall=\frac{3}{5}$

4. 特异度（Specificity ）

（1）什么是特异度？

真实为假例的样本中预测结果为反例的结果

（2）计算公式

$$Specificity=\frac{TN}{FP+TN}$$
在例子中，$Specificity=\frac{4}{5}$

5.F1-score

（1）什么是F1-Score?

模型准确率和召回率的一种加权平均， F1-score的最大值是1，最小值是0。1代表模型输出结果好，0代表模型输出结果差

（2）计算公式

$$F1-Score=\frac{2\ast Precision\ast Recall}{Precision+Recall}$$
在例子中，$F1-score=\frac{2\ast \frac{3}{4}\ast \frac{3}{5}}{\frac{3}{4}+\frac{3}{5}}=\frac{2}{3}$

6.python输出混淆矩阵

还是以上例子

from sklearn.metrics import confusion_matrix

y = [1, 1, 0, 1, 0, 0, 0, 1, 1, 0]
y_pred = [0, 1, 0, 1, 1, 0, 0, 1, 0, 0]

cf_matrix = confusion_matrix(y, y_pred)
print(cf_matrix)

输出结果

2.2 ROC曲线和AUC值

1.ROC曲线的定义

ROC曲线是以[FPR,TPR]的形式在二维坐标中画出的图形，其中FPR是假阳率(假阳数量除以假阳加真阴)，TPR是真阳率(阳数量除以真阳加假阴)，其相关计算公式如下：
$$FPR=\frac{FP}{FP+TN}$$
$$TPR=\frac{TP}{TP+FN}$$
我们对比一下2.1混淆矩阵的定义，TPT对应召回率

2. AUC值

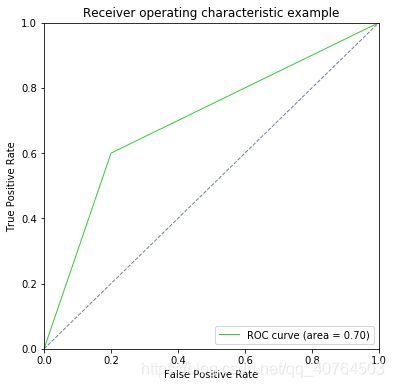
AUC值为ROC曲线下面的面积，取值在[0,1]，越接近1，代表预测效果越好
AUC的一般判断标准：

• 0.1 - 0.5：模型的表现比随机猜测还差
• 0.5 - 0.7：效果较低，但用于预测股票已经很不错了
• 0.7 - 0.85：效果一般
• 0.85 - 0.95：效果很好
• 0.95 - 1：效果非常好，但一般不太可能

3.python绘制ROC曲线及计算AUC值

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc

y = [1, 1, 0, 1, 0, 0, 0, 1, 1, 0]
y_pred = [0, 1, 0, 1, 1, 0, 0, 1, 0, 0]

fpr, tpr, threshold = roc_curve(y, y_pred)  #计算真阳率和假阳率
roc_auc = auc(fpr, tpr)  #计算auc的值


plt.figure(figsize=(6, 6)) #设置画布
#假阳率为横坐标，真阳率为纵坐标做曲线###假阳率为横坐标，真阳率为纵坐标做曲线
plt.plot(fpr, tpr, color='LimeGreen',
         lw=1, label='ROC curve (area = %0.2f)' % roc_auc)  #2表示小数点后位数
plt.plot([0, 1], [0, 1], color='SlateGray', lw=1, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

输出结果

2.3 不平衡数据的影响

1. 不平衡场景下的准确率估计

在不平衡数据集中，准确率并不是一个用来衡量模型性能的合适指标
在一个公用事业欺诈检测数据集中，有以下数据：

总观测 = 1000
欺诈观测（正样本） = 20
非欺诈观测 （负样本）= 980
罕见事件比例 = 2%

在这个例子中，如果一个分类器将所有属于大部分类别的实例都正确分类，实现了 98% 的准确率；而把占 2% 的少数观测数据视为噪声并消除了。但实际上我们真正关心的是被消除的那2%的少数类样本。

所以这种情况下，准确率严重高估了模型的表现。

2. 不平衡场景下的AUC评估

当面临不平衡的数据集的时候，ROC曲线无视样本不均衡的情况，只考虑模型的分类能力。正负样本的比例变化时，模型的区分能力不变，ROC曲线的形状是不会变的。所以对模型在不平衡数据集上的性能评估最好使用AUC而不是Accuray。

3. 不平衡数据对模型表现的影响

在样本不平衡的时候，模型的表现较差，当少数类的比例升高后，模型的AUC迅速提升，分离边界也更加合理，在比例继续升高的时候AUC有少许下降是因为正负样本发生了重叠。

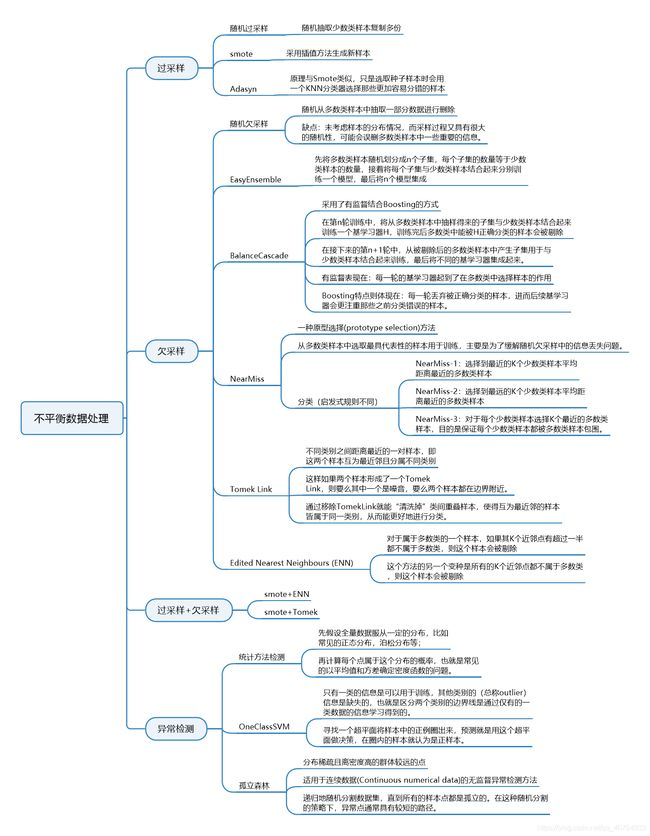
3. 处理不平衡数据的常用方法

3.1 smote算法

1. 算法步骤

(1)对于少数类中每一个样本$x_i$，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其k近邻。

(2)根据样本不平衡比例设置一个采样比例以确定采样倍率$N$，对于每一个少数类样本$x_i$，从其k近邻中随机选择若干个样本，假设选择的近邻为$x_n$。

(3)对于每一个随机选出的近邻$x_n$，分别与原样本按照如下的公式构建新的样本
$x_{new}=x+rand(0,1)(x_n-x)$