转载请注明出处:http://blog.csdn.net/luoshixian099/article/details/47606159
继上一篇中已经介绍了SIFT原理与C源代码剖析,最后得到了一系列特征点,每一个特征点相应一个128维向量。假如如今有两副图片都已经提取到特征点,如今要做的就是匹配上相似的特征点。
相似性查询有两种基本方式:1.范围查询:即给点查询点和查询阈值,从数据集中找出全部与查询点距离小于阈值的点。
2.K近邻查询:给点查询点及正整数K,从数据集中找到与查询点近期的K个数据,当K=1时,就是近期邻查询。
特征匹配算子能够分为两类:1.穷举法:即将数据集中的点与查询点逐一计算距离,假设图1提取到N1个特征点,图2中提取到N2个特征点,用穷举法匹配,要做N1×N2运算。这样的方法显然效率低下。
2.建立数据索引:对数据进行分析。对搜索数据空间进行划分。按划分时是否有重叠,分为KD树和R树。KD树是对空间划分时没有重叠的一种。
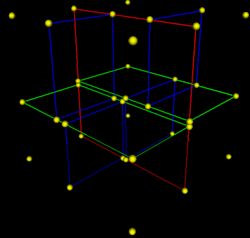
一个三维k-d树。第一次划分(红色)把根节点(白色)划分成两个节点。然后它们分别再次被划分(绿色)为两个子节点。最后这四个子节点的每个都被划分(蓝色)为两个子节点。由于没有更进一步的划分。最后得到的八个节点称为叶子节点。
KD树的构建:KD树是一个二叉树,对数据空间空间进行划分,每个结点相应一个空间范围。
如上图所看到的。三维空间的划分方式。首先确定在数据集上相应方差最大的维度ki,并找到在ki维度上的数据集的中值kv(并作为根节点),即第一步把空间划分成两部分,在第ki维上小于kv的为一部分称为左子节点。大于kv的为另外一部分相应右子节点,,然后再利用相同的方法,对左子结点和右子节点继续构建二叉树,直所剩数据集为空。
举个样例:有5个数据,每一个数据都是5维。建立KD树,A<7,5,7,3,8>;B<3,4,1,2,7>;C<5,2,6,6,9>;D<9,3,2,4,1>,E<2,1,5,1,4>。首先在计算在5个维度上的方差为6.56;2;5.36;2.96;8.56;可见在第5维度上方差最大。继续在第5个维度上找到中值为7,即B点,在第5维度上值小于7的作为左子树数据(A,C),大于7的作为右子树(D,E),然后继续在A,C,两点上计算方差最大的维度,继续划分。
D,E也是如此。例如以下图。ki表示维度,kv表示该维度上的值。
KD树的查询:从根节点開始沿二叉树搜索,直到叶子结点为止。此时该叶节点并不一定是近期的点。可是一定是叶子结点附近的点。所以一定要有回溯的过程,回溯到根节点为止。
比如:查询与M<5,4。1,3,6>点的近期邻点,查询路径为B。A。C,计算完MC的距离后,逆序向上,查询A及A的右子树,再次回溯B及B左子树,最后得到近期的距离,MB点近期。
假如数据集是维数是D,一般来说要求数据的规模N须要满足N>>2^D条件,才干达到高效的搜索。一般来说用标准的KD树时数据集的维数不超过20,可是像SIFT特征描写叙述子128为,SURF描写叙述子为64维,所以要对现有的KD树进行改进。
BBF:上述回溯的过程,全然是依照查询时路径决定的,没有考虑查询路径上的数据性质。BBF(Best-Bin-First)查询机制能确保优先包括近期邻点的空间,即BBF维护了一个优先队列,每一次查询到左子树或右子树的过程中,同一时候计算查询点在该维度的中值的距离差保存在优先队列里,同一时候还有一个孩子节点地址也存入队列里。回溯的过程即从优先队列按(差值)从小到大的顺序依次回溯。
如上一个样例,首先把B保存在优先队列里。然后開始从优先队列里取数据,取出B,发现要到左孩子A节点里继续查询,这时,要把右孩子节点D保存在优先队列里,同一时候加上距离属性ki=5。kv=7。所以d=7-6=1,这时优先队列里简记为D(1);同理,假设A有右孩子。也要存入优先队列,加上属性ki=2,kv=5,d=5-4=1;(样例不太恰当,o(╯□╰)o),回溯的过程是依照优先队列的距离逐个回溯,直到优先队列为空,或者超时,停止。BBF设置了超时机制。为了在高维数据上,满足检索速度的须要以精度换取时间。获得高速查询。这样可知。BBF机制找到的近期邻是近似的,并不是是近期的,仅仅能说是离近期点比較近而已。超时机制在算法的实现上,限定了从优先队列中提取数据的次数。
以下从算法上解析:
构建KD树:
struct kd_node* kdtree_build( struct feature* features, int n )//features为特征带你。n为个数
{
struct kd_node* kd_root;
if( ! features || n <= 0 )
{
fprintf( stderr, "Warning: kdtree_build(): no features, %s, line %d\n",
__FILE__, __LINE__ );
return NULL;
}
kd_root = kd_node_init( features, n ); //建立根节点。每次建立一个节点存入一个特征点
expand_kd_node_subtree( kd_root );//以根节点開始扩展KD树
return kd_root;
}static struct kd_node* kd_node_init( struct feature* features, int n )
{
struct kd_node* kd_node;
kd_node = malloc( sizeof( struct kd_node ) );
memset( kd_node, 0, sizeof( struct kd_node ) );
kd_node->ki = -1; //属性ki初始化为1
kd_node->features = features;//指向特征点
kd_node->n = n; //节点属性n保存以kd_node为根的树上总节点数
return kd_node;
}static void expand_kd_node_subtree( struct kd_node* kd_node ) //递归法建立KD树
{
/* base case: leaf node */
if( kd_node->n == 1 || kd_node->n == 0 ) //假设剩下一个节点,成为叶子节点
{
kd_node->leaf = 1;
return;
}
assign_part_key( kd_node ); //计算最慷慨差的相应的维数,ki和kv
partition_features( kd_node );//按第ki维的数据大小分成左子树数据和右子树的数据
if( kd_node->kd_left ) //继续构建左子树
expand_kd_node_subtree( kd_node->kd_left );
if( kd_node->kd_right )//继续构建右子树
expand_kd_node_subtree( kd_node->kd_right );
}static void assign_part_key( struct kd_node* kd_node ) //计算节点数据的最慷慨差相应的维数ki,和中值kv
{
struct feature* features;
double kv, x, mean, var, var_max = 0;
double* tmp;
int d, n, i, j, ki = 0;
features = kd_node->features;
n = kd_node->n;
d = features[0].d;
/* partition key index is that along which descriptors have most variance */
for( j = 0; j < d; j++ ) //计算d维数据上,全部维数上的方差。
{
mean = var = 0;
for( i = 0; i < n; i++ )
mean += features[i].descr[j];
mean /= n;
for( i = 0; i < n; i++ )
{
x = features[i].descr[j] - mean;
var += x * x;
}
var /= n; //计算第j维的数据的方差
if( var > var_max )
{
ki = j;
var_max = var;
}
}
/* partition key value is median of descriptor values at ki */
tmp = calloc( n, sizeof( double ) );
for( i = 0; i < n; i++ ) //取得全部数据上第ki维上的数据
tmp[i] = features[i].descr[ki];
kv = median_select( tmp, n ); //找到第ki维度上中间的值。这里採用了最坏情况执行时间O(n)的选择算法
free( tmp );
kd_node->ki = ki; //维度
kd_node->kv = kv; //中间值
}static void partition_features( struct kd_node* kd_node )
{
struct feature* features, tmp;
double kv;
int n, ki, p, i, j = -1;
features = kd_node->features;
n = kd_node->n;
ki = kd_node->ki;
kv = kd_node->kv;
for( i = 0; i < n; i++ ) //对特征点按第ki维数据大小排序
if( features[i].descr[ki] <= kv )
{
tmp = features[++j];
features[j] = features[i];
features[i] = tmp;
if( features[j].descr[ki] == kv )
p = j;
}
tmp = features[p];
features[p] = features[j];
features[j] = tmp;
/* if all records fall on same side of partition, make node a leaf */
if( j == n - 1 ) //说明仅仅剩一个节点,标记为叶子节点
{
kd_node->leaf = 1;
return;
}
kd_node->kd_left = kd_node_init( features, j + 1 );//创建左子树,里面有j+1个结点
kd_node->kd_right = kd_node_init( features + ( j + 1 ), ( n - j - 1 ) );//创建右子树,里面有n-j-1个结点
}☆KD树已经创建完成。如今要做的是查询。查询与特征点近期邻的K个特征点,首先把根节点插入到优先队列,然后開始从有优先队列中取元素,遍历到叶节点,同一时候路径过程中。未查询的还有一个结点的增加优先队列(按ki维上的数值与kv的差值的绝对值大小),然后再次从优先队列中取结点,再次遍历到叶节点,如此重复...直到遇到超时限制,或者遍历全然部节点为止。
/*
kd_root为创建好的KD树。feat为要查询的特征点
k为要找到的近邻节点数,SIFT中选取2
nbrs存储查询到的k个近邻数据
max_nn_chkes为最大提取队列次数,即超时限制
成功返回找到的近邻数据个数,否则返回-1
*/
int kdtree_bbf_knn( struct kd_node* kd_root, struct feature* feat, int k,
struct feature*** nbrs, int max_nn_chks )
{
struct kd_node* expl;
struct min_pq* min_pq;
struct feature* tree_feat, ** _nbrs;
struct bbf_data* bbf_data;
int i, t = 0, n = 0;
if( ! nbrs || ! feat || ! kd_root )
{
fprintf( stderr, "Warning: NULL pointer error, %s, line %d\n",
__FILE__, __LINE__ );
return -1;
}
_nbrs = calloc( k, sizeof( struct feature* ) );
min_pq = minpq_init(); //创建一个最小优先队列
minpq_insert( min_pq, kd_root, 0 ); //在优先队列在插入第一个根元素
while( min_pq->n > 0 && t < max_nn_chks ) //假设队列不为空且在超时次数内
{
expl = (struct kd_node*)minpq_extract_min( min_pq );//在优先队列中取出一个元素
if( ! expl )
{
fprintf( stderr, "Warning: PQ unexpectedly empty, %s line %d\n",
__FILE__, __LINE__ );
goto fail;
}
expl = explore_to_leaf( expl, feat, min_pq );// 找到特征点在KD树叶子节点位置,过程中未查询的增加优先队列
if( ! expl )
{
fprintf( stderr, "Warning: PQ unexpectedly empty, %s line %d\n",
__FILE__, __LINE__ );
goto fail;
}
for( i = 0; i < expl->n; i++ ) //遍历以expl为根的子树全部节点
{
//printf("%x",expl->features[i].feature_data);
tree_feat = &expl->features[i];
bbf_data = malloc( sizeof( struct bbf_data ) );
if( ! bbf_data )
{
fprintf( stderr, "Warning: unable to allocate memory,"
" %s line %d\n", __FILE__, __LINE__ );
goto fail;
}
//bbf_data->old_data 这个数据没实用途。由于特征点属性中没有使用到feature_data这个自己定义类型
bbf_data->old_data = tree_feat->feature_data;
printf("%x",bbf_data->old_data);
bbf_data->d = descr_dist_sq(feat, tree_feat); //计算两特征点的欧式距离
tree_feat->feature_data = bbf_data;
n += insert_into_nbr_array( tree_feat, _nbrs, n, k ); //找到K个近邻的特征点,存入数组_nbrs中。从小到大的距离;
}
t++;
}
minpq_release( &min_pq );
for( i = 0; i < n; i++ )
{
bbf_data = _nbrs[i]->feature_data;
_nbrs[i]->feature_data = bbf_data->old_data;
free( bbf_data );
}
*nbrs = _nbrs;
return n;
fail:
minpq_release( &min_pq );
for( i = 0; i < n; i++ )
{
bbf_data = _nbrs[i]->feature_data;
_nbrs[i]->feature_data = bbf_data->old_data;
free( bbf_data );
}
free( _nbrs );
*nbrs = NULL;
return -1;
}struct min_pq* minpq_init() //队列初始化
{
struct min_pq* min_pq;
min_pq = malloc( sizeof( struct min_pq ) );
min_pq->pq_array = calloc( MINPQ_INIT_NALLOCD, sizeof( struct pq_node ) );//分配队列的空间
min_pq->nallocd = MINPQ_INIT_NALLOCD;
min_pq->n = 0;//队列中元素的个数
return min_pq;
}int minpq_insert( struct min_pq* min_pq, void* data, int key )//向优先队列中插入元素
{
int n = min_pq->n;
/* double array allocation if necessary */
if( min_pq->nallocd == n )
{
min_pq->nallocd = array_double( (void**)&min_pq->pq_array,
min_pq->nallocd,
sizeof( struct pq_node ) );
if( ! min_pq->nallocd )
{
fprintf( stderr, "Warning: unable to allocate memory, %s, line %d\n",
__FILE__, __LINE__ );
return 1;
}
}
min_pq->pq_array[n].data = data;
min_pq->pq_array[n].key = INT_MAX;
decrease_pq_node_key( min_pq->pq_array, min_pq->n, key ); //插入元素到优先队列中,堆排序算法
min_pq->n++;
return 0;
}从队列中取出一个节点,沿着结点遍历到叶节点为止,同一时候未查询的增加优先队列。
static struct kd_node* explore_to_leaf( struct kd_node* kd_node, //从kd_node開始開始查询直到叶节点为止
struct feature* feat,
struct min_pq* min_pq )
{
struct kd_node* unexpl, * expl = kd_node;
double kv;
int ki;
while( expl && ! expl->leaf )
{
ki = expl->ki;
kv = expl->kv;
if( ki >= feat->d )
{
fprintf( stderr, "Warning: comparing imcompatible descriptors, %s" \
" line %d\n", __FILE__, __LINE__ );
return NULL;
}
if( feat->descr[ki] <= kv )
{
unexpl = expl->kd_right;
expl = expl->kd_left;
}
else
{
unexpl = expl->kd_left;
expl = expl->kd_right;
}
if( minpq_insert( min_pq, unexpl, ABS( kv - feat->descr[ki] ) ) ) //未查询到的结点,按差值大小增加优先队列
{
fprintf( stderr, "Warning: unable to insert into PQ, %s, line %d\n",
__FILE__, __LINE__ );
return NULL;
}
}
return expl;
}
double descr_dist_sq( struct feature* f1, struct feature* f2 )
{
double diff, dsq = 0;
double* descr1, * descr2;
int i, d;
d = f1->d;
if( f2->d != d )
return DBL_MAX;
descr1 = f1->descr;
descr2 = f2->descr;
for( i = 0; i < d; i++ )
{
diff = descr1[i] - descr2[i];
dsq += diff*diff;
}
return dsq;
}nbrs也是依照从小到大的顺序存储距离,
假如要插入的新的距离为D,队列此时最后一个元素d
1.假设队列未满的情况(即要取得K近邻还没有找到K个)(1) D>=d,直接插入到队列后面;(2) D
2.假设队列已经满了:(1)D>=d,直接丢弃当前的距离;(2)D
static int insert_into_nbr_array( struct feature* feat, struct feature** nbrs,
int n, int k )
{
struct bbf_data* fdata, * ndata;
double dn, df;
int i, ret = 0;
if( n == 0 )
{
nbrs[0] = feat;
return 1;
}
/* check at end of array */
fdata = (struct bbf_data*)feat->feature_data; //推断要插入的位置
df = fdata->d;
ndata = (struct bbf_data*)nbrs[n-1]->feature_data;
dn = ndata->d;
if( df >= dn ) //准备插入到最后
{
if( n == k ) //但K近邻队列已满,舍弃
{
feat->feature_data = fdata->old_data; //舍弃掉前。再次保留之前自己定义的数据
free( fdata );
return 0;
}
nbrs[n] = feat;
return 1;
}
/* find the right place in the array插入到队列中间,分为队列满或不满的情况 */
if( n < k ) //K近邻队列没满,元素向后平移
{
nbrs[n] = nbrs[n-1];
ret = 1;
}
else
{
nbrs[n-1]->feature_data = ndata->old_data;//队列已满。最后一个要舍弃,恢复之前的数据
free( ndata );
}
i = n-2;
while( i >= 0 ) //元素逐次向后平移找到,队列中适当的位置;
{
ndata = (struct bbf_data*)nbrs[i]->feature_data;
dn = ndata->d;
if( dn <= df )
break;
nbrs[i+1] = nbrs[i];
i--;
}
i++;
nbrs[i] = feat; //插入元素
return ret;
}至此,关于SIFT原理以及特征点匹配的算法已介绍完成,兴许文章将陆续更新surf,brife,fast,ORB等一系列关于特征匹配的文章。再次感谢CSDN上的大牛们!