数据压缩：完全重建QMF滤波器组的相关知识

一、完全重建QMF的设计

1.1 完全重建QMF组

完全重建QMF滤波器组最大的优点是在对信号进行抽取后，可以根据每个子带的不同特征分别进行处理，而插值和合成环节又能消除信号失真的各种因素，因此被广泛用于语音处理、图像处理、国防通信和小波变换中。目前，完全重建QMF滤波器组的设计有多种优化设计方法，如特征值法、最小二乘法[1]、遗传法、多项式分解法[2]等等，都将信号失真降到了很小的范围，但是这些方法计算复杂、参数不容易确定、程序编写较难。而利用matlab的信号处理功能和运算功能，可以快速、有效的设计完全重建QMF滤波器组，且具有较高的精度。

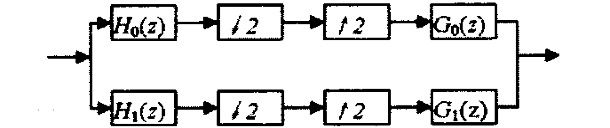
1.2 两通道正交镜像滤波器组理论

在分析滤波器组一侧，输入信号（设为宽带信号）被分成K个子频带信号（窄带信号），通过抽取可降低采样率；在综合滤波器一侧，通过零值内插和带通滤波可以重建原来的信号。

如果综合滤波器组最后输出的信号$x^{{}^{\prime }}(n{T}_1)$与分析滤波器组原来输入的信号$x(n{T}_1)$有如下关系：

那么称$x^{{}^{\prime }}(n{T}_1)$是对$x(n{T}_1)$的完全重建.

这两者之间存在着误差：

1. 混叠失真【由抽取和内插产生的混叠和镜像带来的误差，导致分析滤波器组和综合滤波器组的频带不能完全分开】

2. 幅度失真【由于分析和综合滤波器组的频带在通带内不是全通函数，其幅频特性波纹产生的误差】

3. 相位失真【由滤波器相频特性的非线性所产生的误差】

4. 量化失真【由编、解码产生的误差，与量化噪声相似，这类误差无法完全消除，只能设法减小】

消除混叠失真的方法：

令
$$G_0(z)=H_0(z)$$

$$G_1(z)=-H_1(z)=-H_0(-z)$$

若$H_0(z)$是低通滤波器，那么$H_1(z)$、$G_0(z)$、$G_1(z)$则分别是高通、低通、高通滤波器。

1.3 完全重建QMFB遇到的问题和解决办法

在完全重建QMFB过程中，希望设计的滤波器通带尽量平、过渡带尽量窄，且阻带尽可能快速衰减。在上式指定分析滤波器组的条件下想要做到既无混叠失真又无幅度失真是不可行的，也就是做不到QMFB的完全重建。

解决办法：

（1）用FIR QMF滤波器组，去除相位失真的前提下，尽可能的减小幅度失真，近似实现完全重建；

（2）用IIR QMF滤波器组，去除幅度失真，不考虑相位失真，近似实现完全重建；

（3）修正QMF滤波器$H_1(z)=H_0(-z)$的关系，去考虑更合理的形式，从而实现完全重建

综上分析可知，实现完全重建QMFB并不简单，一般只能做到近似重建，近似程度取决于设计的优化。

1.4 完全重建OMFB的Matlab设计

完全重建QMFB需要找到合适的N和ω的值，使得重建效果最好。为此，首先选定 ω ，对应不同的输入信号x(n) ，改变N的大小求出均方误差mse，通过比较得到最优的N值；其次，固定N，对应不同的输入信号x(n) ，改变 ω 的大小求出均方误差mse，通过比较得到最优的 ω 值。至此，找到了使得完全重建QMFB效果最好的参数N和ω 。

Matlab代码：

N=41;
w=0.43;
[h0,h1,g0,g1]=firpr2chfb(N,w);
[H1z,w]=freqz(h0,1,512);
H1_abs=abs(H1z);H1_db=20*log10(H1_abs);
[H2z,w]=freqz(h1,1,512);
H2_abs=abs(H2z);H2_db=20*log10(H2_abs);
%%%%%%%%%%滤波器h0和h1的幅度响应%%%%%%%%%%
figure(1); 
plot(w/pi,H1_db,'-',w/pi,H2_db,'--'); 
axis([0,1,-100,10]); 
grid 
xlabel('\omega/\pi');ylabel('幅度,dB'); 
sum1=H1_abs.*H1_abs+H2_abs.*H2_abs; 
d=10*log10(sum1);
%%%%%%%%%%%%幅度响应关系误差%%%%%%%%%%%%%
figure(2) 
plot(w/pi,d);grid; 
xlabel('\omega/\pi');ylabel('误差,dB'); 
axis([0,1,-0.04,0.04]); 
%%%%%%%%%%%%%x1(n)%%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(2)=1;x(3)=1;
x(6)=2;x(7)=2;x(8)=2;
x(17)=1.5;x(18)=1.5;x(19)=1.5;
x(24)=1;x(25)=1;
x(33)=3;x(34)=3;x(35)=3;
%%%%%%%%%%%%%%x2(n)%%%%%%%%%%%%%%%%%%%%
x=zeros(1,500);
x(1)=1;x(2)=1;x(3)=1;
x(9)=2;x(10)=2;x(11)=2;
x(16)=3;x(17)=3;x(18)=3;
x(24)=4;x(25)=4;x(26)=4;
x(33)=3;x(34)=3;x(35)=3;
x(41)=2;x(42)=2;x(43)=2;
x(49)=1;x(50)=1;x(51)=1;
%%%%%%%%%%%%%%x3(n)%%%%%%%%%%%%%%%%%%%%
n=1:500;
T=0.2;
x=sin(n*T);
hlp=mfilt.firdecim(2,h0);
hhp=mfilt.firdecim(2,h1);
glp=mfilt.firinterp(2,g0);
ghp=mfilt.firinterp(2,g1);
x0=filter(hlp,x);
x0=filter(glp,x0);
x1=filter(hhp,x);
x1=filter(ghp,x1);
xidle=x0+x1;
xshift=[zeros(1,N) x(1:end-N)];
e=xidle-xshift;
mes=sum(abs(e).^2)/length(e)
fvtool(h0)
%%%%%%%%%%%%输入信号%%%%%%%%%%%%%%%%%%
figure(4);
plot(x);
%%%%%%%%%%理想输出信号与重建输出信号%%%%%%%
figure(5);
axis([0,500,-1,1]); 
plot(xshift,'r');hold on;
plot(xidle,'-');
axis([0,600,-1.1,1.1]);
%%%%%%%理想输出信号与重建输出信号的偏差%%%%%%
%%理想输出信号与重建的输出信号的偏差
figure(6);
plot(xshift-xidle);

结果：

Figure 1:

输出波形为H0和H1的幅度响应，二者是镜像对称的。

Figure 2:

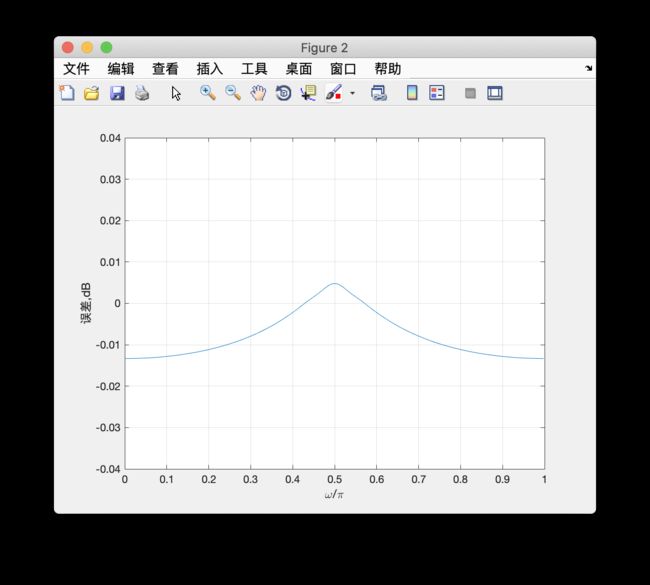
输出的figure则是两者的幅度响应的差值，可以看到，差值并不大。

Figure 3:

输出为H0的幅度响应，可以看到H0近乎为一条直线，并且过渡带很窄，满足要求。

Figure 4、5、6:

Figure4	Figure5	Figure6
原信号	重建的输出信号	原信号和重建信号做差得到的信号

可以发现，理想输出信号与重建输出信号的偏差相对较小「数量级为$10_{-5})$」，因此，可以实现QMFB的近似完全重建。

二、生成100点的序列并进行FFT变换

Matlab代码：

clear all;
close all;
x1=1:15;
x2=15:-1:1;
y1=[1.*x1.^2,1.*x2.^2,ones(1,70)];
m=1:length(y1);

Y1=fft(y1,100);
figure(1)
subplot(221)
stem(y1);
subplot(222)
plot(1:100,abs(Y1));

y2=[ones(1,70),1.*x1.^2,1.*x2.^2];


Y2=fft(y2,100);

subplot(223)
stem(y2);
subplot(224)
plot(1:100,abs(Y2));

结果：

可见，傅里叶变换不能很好的反映时域上不同时间的差别。