深度学习一：深度前馈网络

简述

• 深度前馈网络(deep feedforward network), 又叫前馈神经网络(feedforward neural network)和多层感知机(multilayer perceptron, MLP) .
• 深度前馈网络之所以被称为网络(network)，因为它们通常由许多不同的符合函数组合在一起来表示。
• 由输入层(input layer)、隐藏层(hidden layer)、输出层(output layer)构成。
• 隐藏层的维数决定了模型的宽度(width)。

如图，这是一个经典的二层神经网络模型(Two-Layer Neural Network)。通常输入层和输出层神经元的个数是固定的，我们需要选择和调整隐藏层的层数和每一层神经元的个数等。

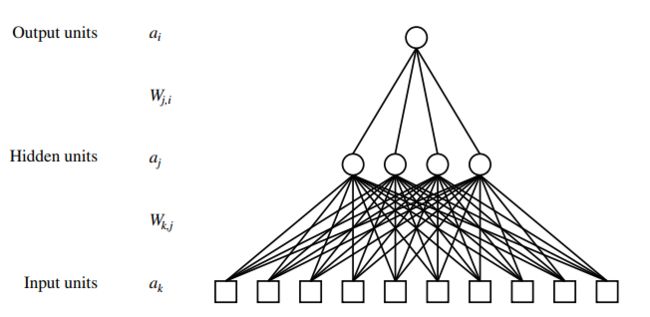
注：我们可以利用矩阵乘法来迅速计算神经网络的输出，后面不会提及。可以参考Python神经网络编程(拉希德著)这本书，写的非常简洁。

线性分类问题

所有数据样本是线性可分的，即满足一个形如 \(w_0+w_1x_1+w_2x_2\)的线性方程的划分

线性分类问题的局限

我们引入经典的逻辑运算来推理线性分类问题的局限。

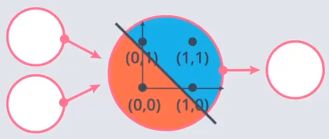
如图所示，分别为线性模型来表示 AND，OR 逻辑，那么XOR要怎么表示呢？

由图可知：我们可以利用线性模型拟合出一个直线来表示 AND、OR、NOR 的逻辑运算，但是没有办法用一条直线表示 xor 异或逻辑，这就是一个经典的非线性问题！

注：黑色点是positive(1)的点，白色点是negative(0)的点

从逻辑运算的视角来看：

逻辑	1 1	0 1	1 0	0 0
AND	1 AND 1 = 1	0 AND 1 = 0	1 AND 0 = 0	0 AND 0 = 0
OR	1 OR 1 = 1	0 OR 1 = 1	1 OR 0 = 1	0 OR 0 = 0
NOR	1 NOR 1 = 0	0 NOR 1 = 0	1 NOR 0 = 0	0 XOR 0 = 1
XOR	1 XOR 1 = 0	0 XOR 1 = 1	1 XOR 0 = 1	0 XOR 0 = 0

我们可以利用如下图所示的一个神经元的感知机来表示一个逻辑 and/or/nor，即每一个神经元可以拟合出一条直线：

解决线性问题的局限

这里涉及感知机(perceptron)的基本思想：多个神经元拟合多条直线，将这些直线组合在一起来划分一个非线性的边界。
我们来看上面的XOR逻辑，作为一个简单的例子，发现

\[I_1 XOR I_2 \]

可以表示为

\[(I_1 AND I_2) NOR (I_1 NOR I_2)。 \]

根据上述公式和图，我们可以画出如下的多层感知机，来实现非线性划分数据表示XOR逻辑关系。

非线性问题常规处理手段

特征非线性

引入非线性的特征来处理非线性问题。
例如：输入节点有表示平方的节点等。

模型非线性

引入非线性的激活函数来处理非线性问题。

激活函数

激活函数(activation function)又叫转移函数(transfer function)，用来增加神经网络模型的非线性。

\[activation_i = g(s_i) = g(\sum_{j}w_{ij}x_j) \]

下图是只有一个神经元的示意图：g函数是非线性的激活函数。由图中可以看出，当神经元计算出线性方程的结果s之后，传入激活函数g中进行处理，最终得到神经元的输出g(s)，从而实现非线性。

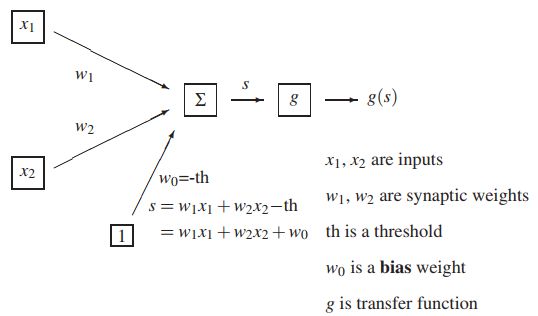
常用的激活函数

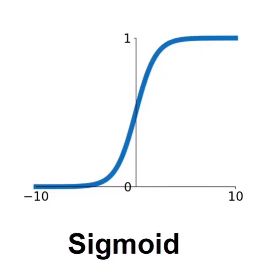
Sigmoid

S型激活函数又叫挤压函数，可以把任意的大小的x挤压到(0,1)之间的y, 在x增大或者减小的过程中会逐渐出现饱和(无限趋近于0或者1)。
在二分类问题中，可以以0.5为阈值，小于0.5为一个类别，大于0.5为另一个类别。

\[f(x) = \frac{1}{1 + e^{-x}} \]

缺点：

1. 存在饱和现象，会导致梯度消失。
2. 优化路径存在zig zag问题。
3. 函数使用指数运算，运算量比较大。

Tanh

双曲正切函数，与sigmoid函数相似，也会出现梯度饱和，但是tanh的值域为(-1,1)。

\[tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \]

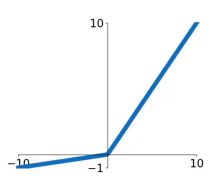
Relu

线性整流函数(Rectified Linear Unit，ReLU)，又称修正线性单元。当x<0时，y为0；当x>0时，y=x。没有饱和现象，y可以取到无穷大。

\[f(x) = max(0,x) \]

优点：

1. 运算速度比较快。
2. 不会出现饱和现象。
3. 收敛迅速。

缺点：

1. 当x<0，y也为0，梯度为0。即当x<0，是没有办法进行学习的。

ELU

指数线性单元(Exponential Linear Unit)也是ReLU激活函数的变体。

\[f(x) = \begin{cases} x & x\geq0 \\ α*(e^x-1) & x<0 \end{cases} \]

优点：

1. 当x<0时，曲线也有变化，不会停止学习。

缺点：

1. 指数运算的计算量比较大。

Leaky ReLU

带泄露修正线性单元(Leaky ReLU)函数是ReLU激活函数的变体。当x<0时，y=0.1x；当x>0时，y=x。

\[f(x) = max(αx,x) \]

优点：

1. 当x<0时，曲线也有变化，不会停止学习。
2. 计算量比ELU小很多
3. x<0的斜率α可以自己设置

反向传播

链式求导

链式求导是反向传播利用的主要数学技巧，因此先来看链式求导。

我们假设

\[y = y(u)\\ u = u(x) \]

即

\[\frac{∂y}{∂x} =\frac{∂y}{∂u}\frac{∂u}{∂x} \]

利用链式求导法则可以有效的求出偏导数。注：应用在神经网络中损失函数必须是可微的（differentiable），例如 Sigmod 或者 Tanh 等

• Sigmod：
  • if $$z(s) = \frac{1}{1+e^-s}$$ , then $$z'(s) = z(1-z)$$
• Tanh:
  • if $$z(s) = tanh(s)$$ , then $$z'(s) = 1-z^2$$

反向传播 Backpropagation

反向传播(back propagation, 简称backprop)。是梯度下降法在深度网络上的具体实现方式。在传统的前馈神经网络中，信息通过网络向前流动，输入x提供初始值，然后传播到每一层的隐藏单元，最终产生输出y。这个流程被称为前向传播(forward propagation)。而反向传播允许来自代价函数的信息通过网络向后流动，以便计算梯度、调整参数。

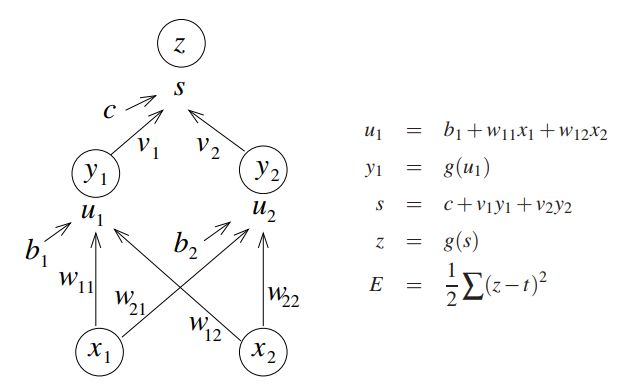
如图，这是一个前向传播网络的示意图：

其中 E 表示计算出的误差，这个例子中利用的是最小均方误差。

我们为了减小误差，使模型的输出接近我们想要的值，就要利用反向传播的办法来调整模型中的参数。将误差信号沿着原来的路线返回，即要从输出到输入做偏导，修改神经元的权值和偏置值，使误差 E 最小。

反向传播中的核心方程

根据上述的方程，我们可以来更新权重，\(w = w - η \frac{∂E}{∂w}\), 其中 \(η\) 是学习率

注：这个地方可能用计算图理解比较清晰。大家可以去查一些相关资料。

损失函数

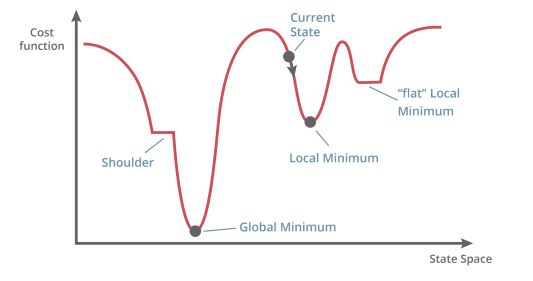
损失函数（Loss Function）又称误差函数（Error Function）和代价函数（Cost Function）

在神经网络中，我们的目标是找到一组权重，使误差最小化，即到达图中的 Global Minimum 点

均方误差 MSE

处理回归问题常用的损失函数

均方误差（Mean Square Error， MSE）是真实值与预测值的差值的平方然后求和平均。

\[E = \frac{1}{2}(z_i-t_i)^2 \]

其中，\(z_i\) 是实际输出值，\(t_i\) 是目标输出值。前面加 \(\frac{1}{2}\) 的原因是为了求导时候消去导数上移下来的数字2.

存在的问题：对于均方误差函数，在处理分类问题的时候不太合适。当 MSE 配合 Sigmoid 函数使用时，MSE 在求导过程中要用到 Sigmoid 函数的导数\(z'(s)\)，会因为梯度消失而导致模型权重学习的很慢。如图

\[\frac{\delta E}{\delta w} = \frac{\delta E}{\delta z} \frac{\delta z}{\delta s} \frac{\delta s}{\delta w} = (z_i-t_i)·z_i'(s)·x_i \]

而交叉熵损失函数可以很好的避免这个问题。

交叉熵损失函数 CEE

处理分类问题常用的损失函数

交叉熵损失函数（Cross Entropy， CE）或称交叉熵误差（Cross Entropy Error， CEE）

\[E = -\sum_kt_klog(z_k) \]

在01二分类问题中，公式形式为

\[E = -tlog(z)-(1-t)log(1-z) \]

常见面试题

用Python手写反向传播神经网络

源码已上传Github, 点击跳转

激活函数的作用

神经网络中的激活函数有哪些

神经网络为什么用交叉熵

交叉熵公式

Loss Function有哪些，怎么用？

线性回归的表达式，损失函数