深度循环神经网络和双向循环神经网络学习笔记

深度循环神经网络和双向循环神经网络

1、深度循环神经网络

本章到目前为止介绍的循环神经网络只有一个单向的隐藏层，在深度学习应用里，我们通常会用到含有多个隐藏层的循环神经网络，也称作深度循环神经网络。图6.11演示了一个有 个隐藏层的深度循环神经网络，每个隐藏状态不不断传递至当前层的下一时间步和当前时间步的下一层。

如下图

$$\begin{gathered} {\mathbf{H}}_t^{(1)}=\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}^{(1)}+{\mathbf{H}}_{t-1}^{(1)}{\mathbf{W}}_{hh}^{(1)}+{\mathbf{b}}_h^{(1)}) \\ {\mathbf{H}}_t^{(\ell )}=\varphi ({\mathbf{H}}_t^{(\ell -1)}{\mathbf{W}}_{xh}^{(\ell )}+{\mathbf{H}}_{t-1}^{(\ell )}{\mathbf{W}}_{hh}^{(\ell )}+{\mathbf{b}}_h^{(\ell )}) \\ {\mathbf{O}}_t={\mathbf{H}}_t^{(L)}{\mathbf{W}}_{hq}+{\mathbf{b}}_q \end{gathered}$$
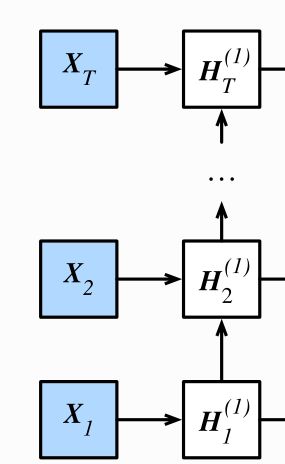
我们之前学的到的循环神经网络都单隐藏层的，如下图

• 具体来说就是，将X1输入到第一个循环神经元H1，这个rnn神经元可以是GRU也可以是LSTM，这里的H1是第一个时间步输出的隐藏状态，其将作为第二个时间步的输入隐藏状态，隐藏状态就这样一直往上传，直到HT。每个Hi（i=1,2,3…T）之后都会接一个输出层output（Oi i=1,2,3…T)，这就是之前的单隐层RNN。

• 对于深度循环神经网络，只是将第一层的每个隐藏状态Hi（i=1,2,3…T），做为第二层的输入，最后。H的上标表示层数，下标表示时间步数。在第L层之后做输出。

部分代码 加上num_layers即可食用 (两层的)

num_hiddens=256
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']

#lr = 1e-2  注意调整学习率
#只需要在nn.LSTM原来的基础上加上参数num_layers=2,即可变成两层的循环神经网络(输入层+两个隐层+输出层)
gru_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens,num_layers=2)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
                                corpus_indices, idx_to_char, char_to_idx,
                                num_epochs, num_steps, lr, clipping_theta,
                                batch_size, pred_period, pred_len, prefixes)

部分代码 (六层的)

gru_layer = nn.LSTM(input_size=vocab_size, hidden_size=num_hiddens,num_layers=6)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
                                corpus_indices, idx_to_char, char_to_idx,
                                num_epochs, num_steps, lr, clipping_theta,
                                batch_size, pred_period, pred_len, prefixes)

实践证明，上边num_layers=2的结果要比num_layers=6的结果要好很多的，所以说深度循环网络不是越深越好。

越深表示模型越复杂，对数据集的要求更高，内容更加抽象。所以参数的设置还要看实践和经验。

小结

• 在深度循环神经网络中，隐藏状态的信息不断传递至当前层的下一时间步和当前时间步的下一层。

---

2、双向循环神经网络

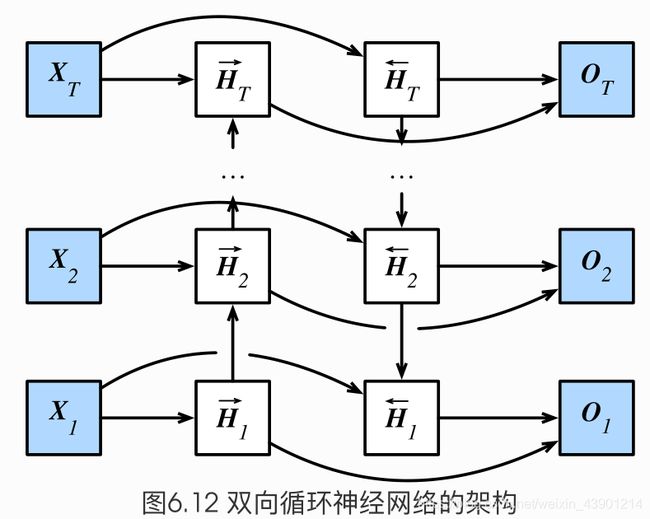
之前介绍的循环神经网络模型都是假设当前时间步是由前面的较早时间步的序列决定的，因此它们都将信息通过隐藏状态从前往后传递。有时候，当前时间步也可能由后⾯面时间步决定。例如，当我们写下一个句子时，可能会根据句子后面的词来修改句子前面的用词。双向循环神经网络通过增加从后往前传递信息的隐藏层来更灵活地处理这类信息。

图6.12演示了一个含单隐藏层的双向循环神经网络的架构。

$$\begin{array}{rl}{\mathbf{H}}_t& =\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}^{(f)}+{\mathbf{H}}_{t-1}{\mathbf{W}}_{hh}^{(f)}+{\mathbf{b}}_h^{(f)})\\ {\mathbf{H}}_t& =\varphi ({\mathbf{X}}_t{\mathbf{W}}_{xh}^{(b)}+{\mathbf{H}}_{t+1}{\mathbf{W}}_{hh}^{(b)}+{\mathbf{b}}_h^{(b)})\end{array}$$

$${\mathbf{H}}_t=({\mathbf{H}}_t,{\mathbf{H}}_t)$$

$${\mathbf{O}}_t={\mathbf{H}}_t{\mathbf{W}}_{hq}+{\mathbf{b}}_q$$

• 我们可以分别计算正向隐藏状态（→）和反向隐藏状态（←）

• 两个方向的隐藏层的连接方式是 concat 拼接起来，蕴含了两个方向的信息 ，根据上图可以想成一个信息往上传，一个信息往下传。

• 不同方向上的隐藏单元个数也可以不同。

• 双向循环神经网络的好处：比如 X 1 到 X T 是一句话，本来我们只考虑了一个方向，即前面的字对后面的字影响。如果是双向的，那么每个字都会受到前面的字和后面的字的影响

很简单 加上 bidirectional=True 即可食用：

num_hiddens=128
num_epochs, num_steps, batch_size, lr, clipping_theta = 160, 35, 32, 1e-2, 1e-2
pred_period, pred_len, prefixes = 40, 50, ['分开', '不分开']

lr = 1e-2 # 注意调整学习率
#设置bidirectional=True 即可构建双向循环神经网络
gru_layer = nn.GRU(input_size=vocab_size, hidden_size=num_hiddens,bidirectional=True)
model = d2l.RNNModel(gru_layer, vocab_size).to(device)
d2l.train_and_predict_rnn_pytorch(model, num_hiddens, vocab_size, device,
                                corpus_indices, idx_to_char, char_to_idx,
                                num_epochs, num_steps, lr, clipping_theta,
                                batch_size, pred_period, pred_len, prefixes)

实践证明，双向带来了更多得参数，效果未必会好。

双向RNN是很常见的，但是否适用还需要实践来看效果。

小结

双向循环神经网络在每个时间步的隐藏状态同时取决于该时间步之前和之后的子序列（包括当前
时间步的输入）。