RSA-OAEP 基于python实现

前言

原本准备用C写的，因为在阅读原理时又担心unsigned long long会越界，C语言计算位数等问题准备先用python试一下。

顺便附一下在搜索C语言有关Miracle库时获得的信息。

啊图放错了 (×)，这就换。

虽然无法理解python运行速度还能比C快? 但还是决定自己去对比下。于是拿出了本以封存的python。

所有代码开源在Gayhub。
食用方法：m,c为bytes，各种密钥都是数字。

RSA算法简介

这个实在是原理简单资料齐全，客官要不试试这个神奇的网站

符号表

c密文代表，是一个界于 0~n-1 之间的整数。
C 密文，是一个八位组串
dRSA 私有幂
eRSA 公开幂
EM 编码后的消息，是一个八位组串
Hash 哈希函数(本篇采用sha1)
hLen 散列函数 Hash 的输出的以八位组为计量单位的长度
k RSA 合数模 n 的以八位组为计量单位的长度
KRSA 私钥
L可选的 RSAES-OAEP 标签，是一个八位组串
m消息代表，是一个界于 0 到 n – 1 的整数
M消息，是一个八位组串
mask MGF 的输出，是一个字节串
maskLen （期望的）掩模的以八位组为计量单位的长度
MGF 掩模生成函数
mgfSeed 生成掩模的种子因数（seed），是一个八位组串
mLen 消息 M 的以八位组为计量单位的长度
nRSA 合数模， n = p * q
(n, e) RSA 公钥
p, q RSA 合数模 n 的前两个素数因子
qInv CRT 系数，是个满足下式且小于 p 的正整数，q · qInv =1 (mod p) 。
X 与 x 对应的一个八位组串
xLen （指定的）八位组串 X 的长度
|| 二进制串拼接

事先准备好的函数

import hashlib
def get_str_sha1_secret_str(res):
    """
    使用sha1加密算法，返回bytes加密后的hex字符串
    """
    sha = hashlib.sha1(res)
    encrypts = sha.hexdigest()
    return encrypts

sha1加密，作为本模型的hash函数，输出定为40字节。

rsa.encode(n,d,m):
	return c

rsa.decode(K,c):
	return m

RSA基本加解密，见文件my_rsa.py。

加密

RSAES-OAEP-ENCRYPT ((n, e), M, L)

元素

可选项	Hash	哈希函数（hLen 表示散列函数输出的字节长度）
	MGF	掩模生成函数
输入	(n, e)	接收方的 RSA 公钥（k 表示 RSA 合数模 n 的字节长度）
	M	待加密的消息，是一个长度为 mLen 的八位组串，其中 mLen <= k – 2hLen – 2
	L	消息的可选附加标签；如果没有提供 L，那么 L 的默认值是空串
输出	C	密文，一个长度为 k 的八位组串

出错提示： “消息太长”；“标签太长”

步骤：

1. 长度检查： a.如果 L 的长度超出哈希函数的输入限制 （SHA-1 的限制是 261 – 1 个八位组），
   输出“标签太长”然后终止运算。 b.如果 mLen > k – 2hLen – 2，输出“消息太长”然后终止运算。

2. EME-OAEP 编码：
   a.如果没有提供标签 L， 则让 L 为空串。 让 lHash = Hash (L)， 这是一个长度为 hLen 的八位组串
   b.生成一个由 k – mLen – 2hLen – 2 个零值八元组构成的串 PS。 PS 的长度可能是零。
   c.连接 lHash，PS，十六进制值为 0x01 的八元组和消息 M ，形成一个长度为 k – hLen – 1 个八位组的数据块 DB = lHash || PS || 0x01 || M 。
   d.生成一个长度为 hLen 的随机八位组串 seed 。
   e.使 dbMask = MGF (seed, k – hLen – 1)
   f.使 maskedDB = DB ^ dbMask.
   g.使 seedMask = MGF (maskedDB, hLen).
   h.使 maskedSeed = seed ^ seedMask.
   i. 连接一个十六进制值为 0x00 的八位组， maskedSeed 和 maskedDB ，形成一个长度为 k 个八位组的编码消息 EM = 0x00 || maskedSeed || maskedDB。

3. RSA 加密：
   将编码消息 EM 转换成一个整数消息代表，m = int(EM) 。
   将 RSA 公钥(n, e) 和消息代表 m 代入RSAEP 加密原语，产生一个整数的密文代表 c ，c = rsa.encode ((n, e), m) 。
   将密文代表 c 转换为一个长度为 k 个八元组的密文 C ，C = bytes (c, k) 。

4. 输出密文 C。

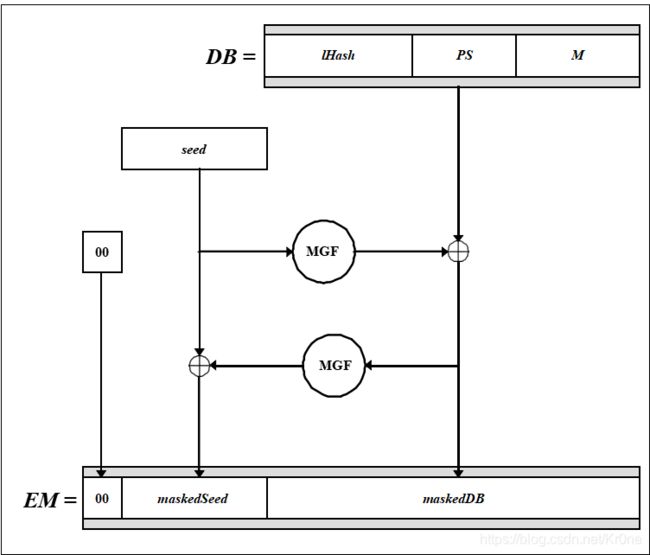
流程图

def oeap_encode(n,e,m,l=b''):
    n_hex = hex(n)[2:]
    if len(n_hex)&1 == 1:
        n_hex = '0' + n_hex
    k = len(n_hex)//2
    hLen = 20
    mLen = len(m)
    if mLen>(k-2-2*hLen):
        return 'Too long message!\n'
    
    lhash = get_str_sha1_secret_str(l)
    if (k - mLen - 2*hLen - 2)>0:
        ps = '00' * (k - mLen - 2*hLen - 2) + '01'
    else:
        ps = '01'
    DB = lhash + ps + m.hex()
    seed = g_seed(hLen)
    dbMask = MGF(seed,k - hLen -1,hLen)
    maskedDB = hex_xor(dbMask,DB,(k-hLen-1)*2) 
    seedMask = MGF (maskedDB, hLen,hLen)
    maskedSeed = hex_xor(seed ,seedMask ,hLen*2)
    EM = '00' + maskedSeed + maskedDB
    return EM

def MGF(x,maskLen,hLen):
    T=bytearray(b'')
    k = maskLen // hLen
    if len(x)&1 == 1:
        x= '0'+x
    X = bytearray.fromhex(x)
    if maskLen%hLen == 0:
        k -= 1
    for i in range(k+1):
        tmp = X + bytearray.fromhex('%08x'%i)
        T = T + bytearray.fromhex(get_str_sha1_secret_str(tmp))
    mask = T[:maskLen]
    return mask.hex()



def g_seed(hLen):
    b = bytearray(hLen)
    for i in range(hLen):
        b[i] = random.randint(0,255)
    return b.hex()

解密

RSAES-OAEP-DECRYPT (K, C, L)

元素

可选项	Hash	哈希函数（hLen 表示散列函数输出的字节长度）
	MGF	掩模生成函数
输入	K	接受方的 RSA 私钥（k 表示 RSA 合数模 n 的以八位组为计量单位的长度）
	C	待解密的密文，使一个长度为 k 的八位组串，其中 k ≥ 2hLen + 2
	L	消息的可选附加标签；如果没有提供 L，那么 L 的默认值是空串
输出	C	密文，一个长度为 k 的八位组串

出错提示： “解密出错”

步骤

1. 长度检查：
   a.如果 L 的长度大于散列函数的输入限制（SHA-1 的限制是 261 – 1 个八位组），输出“解密出错”并中止运算。
   b.如果密文 C 的长度不是 k 个八位组，则输出“解密出错”并中止运算。
   c.如果 k < 2hLen + 2，则输出“解密出错”并中止运算。

2. RSA 解密：
   a.将密文 C 转换成一个整数密文代表 c：c = int © 。
   b.将 RSA 私钥 K 和密文代表 c 代入 RSADP 解密原语，从而产生一个整数消息代表 m：
   m = rsa.decode (K, c) 。
   如果RSADP 输出“密文代表超出范围”（意思是 c ^ n），则输出“解密出错”并且中止运算。
   c.将消息代表 m 转换成一个长度为 k 个八位组的编码消息 EM = int (m, k) 。

3. EME-OAEP 编码：
   a.如果未提供标签 L 的值，则使 L 的值为空串。使 lHash = Hash (L)，这是一个长度为 hLen
   的八位组串。
   b.将编码消息 EM 分解为一个八位组 Y，一个长度为 hLen 的八位组串 maskedSeed，以及一个长度为 k – hLen – 1 的八位组串 maskedDB，使得
   EM = Y || maskedSeed || maskedDB 。
   c.使 seedMask = MGF (maskedDB, hLen).
   d.使 seed = maskedSeed ^ seedMask.
   e.使 dbMask = MGF (seed, k – hLen – 1).
   f.使 DB = maskedDB ^ dbMask.
   g.将 DB 分解成一个长度为 hLen 的八位组串 lHash’，一个（可能为空的）由十六进制值为
   0x00 的八位组构成的填充 PS，以及一个消息 M，使得DB = lHash’ || PS || 0x01 || M .
   如果没有可以从 M 中分离出 PS 的十六进制值为 0x01 的八位组，如果 lHash 没有等同的
   lHash’，或者如果 Y 是非零的，则输出“解密出错”并中止运算。

4. 输出消息 M。

代码

解密部分代码就不贴了。

总结

原理

在实现了python代码后发现，确实在使用MGF时会出现大数，预计不得不使用GMP或者Miracle，待日后RSA-PSS再说了。

代码

优化

可以看到笔者用了很多繁琐的hex与bytearray互换，原因是担心前导0的丢失；但是最后总览时发现位数其实都是固定的，因此可以舍去所有转换，写一个bytes_xor()函数，应该能很大优化代码。不过本着偷懒的因素这次就不优化了。

坑点

1. bytearray.fromhex()函数要求str长度为偶数，且应该舍去开头的’0x’。
2. hex化后长度会和原理中定义的字节长度不一样，关系是简单的二倍关系。