CSP-S2019提高组初赛难点整理

选择题

1. 由数字 $1,1,2,4,8,8$ 组成的不同的 $4$ 位数的个数是 ( )。

【解析】枚举找规律

• 由$1,2,4,8$组成的$4$位数的个数是$A_4^4=24$
• 由$1,1,2,4$组成的$4$位数有：1124,1142,1214,1241,1412,1421,2114,2141,2411,4112,4121,4211，共$12$个
• 由$1,1,2,8$组成的$4$位数的个数是$12$个
• 由$1,1,4,8$组成的$4$位数的个数是$12$个
• 由$8,8,1,2$组成的$4$位数的个数是$12$个
• 由$8,8,1,4$组成的$4$位数的个数是$12$个
• 由$8,8,2,4$组成的$4$位数的个数是$12$个
• 由$1,1,8,8$组成的$4$位数有：1188,1818,1881,8118,8181,8811，共$6$个
  答案为： $24+12\times 6+6=$102。

【扩展】有重复数字的不重复全排列问题：
例如：1 1 2 4这三个数只有12种全排列
分别为：1124,1142,1214,1241,1412,1421,2114,2141,2411,4112,4121,4211，共$12$个。
设第$i$个数有$a_i$个
$ans=\frac{n!}{a_1!a_2!a_3!\cdots a_n!}$

2. $G$ 是一个非连通无向图（没有重边和自环），共有 $28$条边，则该图至少有 ( )个顶点。

【解析】非连通无向图在边数一定的情况下，求最少顶点个数，可以让$1$个顶点与其它顶点不连通，剩下的顶点组成一个完全图时满足顶点个数最少。此时，完全图的顶点个数为$8$个，加上剩下的$1$个点，该图至少有9个顶点。

3. 一些数字可以颠倒过来看，例如 $0$、$1$、$8$ 颠倒过来还是本身，$6$ 颠倒过来是 $9$，$9$ 颠倒过来看还是 $6$，其他数字颠倒过来都不构成数字。类似的，一些多位数也可以颠倒过来看，比如 $106$ 颠倒过来是 $901$。假设某个城市的车牌只由 $5$ 位数字组成，每一位都可以取 $0$ 到 $9$。请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌，并且车牌上的 $5$ 位数能被 $3$ 整除 ( )的车牌号个数。

【解析】5位数车牌倒过来恰好还是原来的数字，那么中间位只能是 $0$、$1$、$8$。确定了车牌前$2$位，后$2$位可以通过找其颠倒过来的相同的数字即可，可选的数字有： $0$、$1$、$8$、$6$、$9$。除此之外，还要保证车牌上的 $5$ 位数能被 $3$ 整除，数据规模较小，可以一一枚举。

• 中间数字是0的情况，00、06、60、09、90、18、81、66、69、96、99，共$11$种。
• 中间数字是1的情况，01、10、16、61、19、91、88，共7种
• 中间数字是8的情况，08、80、11、68、86、89、98、共7种。

答案为：$11+7+7=$25。

4. 有一个等比数列，共有奇数项，其中第一项和最后一项分别是 $2$ 和 $118098$，中间一项是 $486$，请问以下那个数是可能的公比 ( )。

【解析】等比数列，最基本的特点就是数列从第二项开始，每一项与前一项的比值，都是一个定值。比如数列{1,2,4,8,16，……}，后一项与前一项的比值都是 2，那么这就是一个等比数列。
等比数列的通项公式是：$a_n=a_1\times q^{n-1}$
$486$的标准分解式$=2^1\times 3^5$，由此可见公比为3。

阅读程序

#include 
using namespace std;
int n;
int a[100];

int main() {
     
   scanf("%d", &n);
   for (int i = 1; i <= n; ++i)
       scanf("%d", &a[i]);
   int ans = 1;
   for (int i = 1; i <= n; ++i) {
     
       if (i > 1 && a[i] < a[i - 1]) //第12行
            ans = i;
        while (ans < n && a[i] >= a[ans + 1]) //第14行
            ++ans;
        printf("%d", ans);  //第16行
   }
   return 0;
}

第 $16$ 行输出 ans 时，ans 的值一定大于 i。错误

【解析】举相反的情况。当a[]是一个严格单调上升序列时，ans 始终等于i。

若将第 $12$ 行的 “<” 改为 “!=” 程序输出的结果不会改变。正确

【解析】算法是在数组a[]中找到i位置及其右边的连续序列中最后一个小于等于a[i]的数的位置。实现的关键在于 while ()循环中，所以第12行代码，对于最终结果没有影响。

当程序执行到第 $16$ 行时，若 $ans-i>2$，则 $a[i+1]\le a[i]$。正确

【解析】若 $ans-i>2$，说明14行的while()循环至少执行了3次，那么a[i+1]一定小于等于a[i]。

若输入的 a 数组是一个严格单调递增的数列，此程序的时间复杂度是：$O(n)$。

【解析】 当a 数组是一个严格单调递增的数列时，while()`循环一次都不执行，所以程序的时间复杂度是：$O(n)$。

最坏情况下，此程序的时间复杂度为：$O(n^2)$

【解析】 最坏情况下，当a 数组是一个严格单调递减的数列时，while()会执行$n-1,n-2,n-3...$，所以程序的时间复杂度是：$O(n^2)$。

#include 
using namespace std;

const int maxn = 1000;
int n;
int fa[maxn], cnt[maxn];

int getRoot(int v) {
     
    if (fa[v] == v) return v;
    return getRoot(fa[v]);
}

int main() {
     
    cin >> n;
    for (int i = 0; i < n; i++) {
     
        fa[i] = i;
        cnt[i] = 1;
    }
    int ans = 0;
    for (int i = 0; i < n - 1; ++i) {
     
        int a, b, x, y;
        cin >> a >> b;
        x = getRoot(a);
        y = getRoot(b);
        ans += cnt[x] * cnt[y]; //第25行
        fa[x] = y;
        cnt[y] += cnt[x];
    }
    cout << ans << endl;
    return 0;
}

【解析】并查集实现集合集合合并。

若输入的 $a$ 和 $b$ 值均在 $[0,n-1]$的范围内，则对于任意 $0\le i<n$，都有 $1\le cnt[i]\le n$。错误

【解析】$cnt[i]$表示集合中点的个数，若输入的 $a$ 和 $b$ 值均在 $[0,n-1]$的范围内， $a$ 和 $b$ 可能已经属于同一集合，若将同一个集合合并两次，那么cnt[i]中点的数量可能超过$n$。

当 $n$ 等于 $50$ 时，若 $a$、$b$ 的值都在 $[0,49]$ 的范围内，且在第 $25$ 行时$x$总是不等于 $y$，那么输出为 ( )：

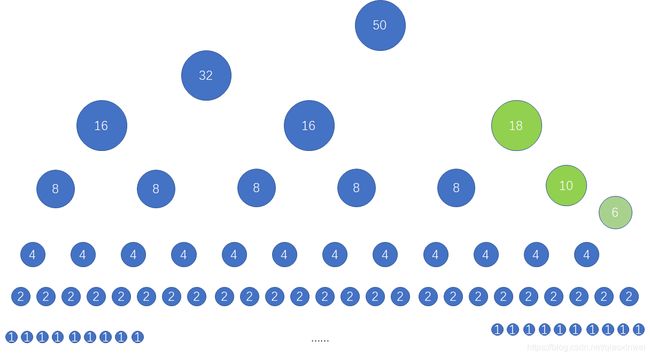
【解析】第 $25$ 行时$x$总是不等于 $y$，保证了总是将两个不同的集合合并，那么合并过程如下图所示：

从下向上依次合并：

• 第一层，$50$个$1$两两相乘，$ans=25$
• 第二层，$24$个$2$两两相乘，$ans=25+12\times 4=73$，合并之后，再将其中的一个$4$和剩余的一个$2$合并，$ans=73+8=81$
• 第三层，$10$个$4$两两相乘，$ans=81+5\times 16=161$，合并之后，再将剩余的一个$4$和剩余的$6$合并，$ans=161+24=185$
• 第四层，$4$个$8$两两相乘，$ans=185+2\times 64=313$，合并之后，再将
  剩余的一个$8$和$10$合并，$ans=313+80=393$
• 第五层，$2$个$16$相乘，$ans=393+16\times 16=649$，合并之后，再将$32$和$18$合并，$ans=649+32\times 18=1225$

答案：1225

此程序的时间复杂度是（ $O(n^2)$）。

【解析】未优化的并查集，在最坏情况下退化称为一个链表，时间复杂度为$O(n^2)$。

2. 本题$t$是$s$的子序列的意思是：从$s$中删去若干个字符，可以得到$t$。特别的，如果$s$ == $t$，那么$t$也是$s$的子序列；空串是任何串的子序列。例如“acd”是“abcde”的子序列，“acd”是“acd”的子序列，但“acd”不是“abcde”的子序列。
   $S[x..y]$表示$s[x]\dots s[y]$共 $y-x+1$ 个字符构成的字符串，若 $x>y$ 则$s[x..y]$是空串。$t[x..y]$同理。

#include 
#include 
using namespace std;
const int max1 = 202;
string s, t;
int pre[max1], suf[max1];

int main() {
     
    cin >> s >> t;
    int slen = s.length(), tlen= t.length();
    for (int i = 0, j = 0; i < slen; ++i) {
     
        if (j < tlen && s[i] == t[j]) ++j;
        pre[i] = j;// t[0..j-1]是s[0..i]的子序列
    }
    for (int i = slen - 1, j = tlen - 1; i >= 0; --i) {
     
        if(j >= 0 && s[i] == t[j]) --j; //第16行
        suf[i]= j; //t[j+1..tlen-1]是s[i..slen-1]的子序列，第17行
    }
    suf[slen] = tlen -1;
    int ans = 0;
    for (int i = 0, j = 0, tmp= 0; i <= slen; ++i) {
     
        while (j <= slen && tmp >= suf[j] + 1) ++j; //第22行
        ans = max(ans, j - i - 1); //第23行
        tmp = pre[i];
    }
    cout << ans << endl;
    return 0;
}

提示：
t[0..pre[i]-1]是s[0..i]的子序列；
t[suf[i]+1..tlen-1]是s[i..slen-1]的子序列。

【解析】pre[i]表示s[0..i]至多可以从前往后匹配到t串的哪一个字符，此时t[0…pre[i]-1]是s[0…i]的子序列。suf[i]用于记录s[i..slen-1]至多从后到前匹配到t的哪一个字符，此时t[suf[i]+1..tlen-1]是s[i..slen-1]的子序列。本题是求s中连续删除至多几个字母后，t仍然是s的子序列。

程序输出时，suf数组满足：对任意 $0\le i<slen,suf[i]\le suf[i+1]$。正确

【解析】从16、17行的代码中可以看出，随着i不断减小，如果s[i] == t[j]，j会减小；否则j不变，说明$suf[i]\le suf[i+1]$

当 t 是 s 的子序列时，输出一定不为 $0$。错误

【解析】手动模拟，s = "a", t = "a"时，此时ans = 0。

程序运行到第 $23$ 行时，j - i - 1 一定不小于 $0$。错误

【解析】手动模拟，s = "a", t = "b"时，j - i - 1 可以为$-1$。

当 t 是 s 的子序列时，pre 数组和 suf 数组满足：对任意 $0\le i<slen$，$pre[i]>suf[i+1]$。错误

【解析】由含义可知若t是s子序列，t[0..pre[i]-1],t[sub[i+1]+1..lent-1]是s[0..i],s[i+1..lens-1]的子序列，不会重叠，即$pre[i]-1<suf[i+1]+1$,即$pre[i]<=suf[i+1]+1$。

若 tlen = 10，输出为 $0$ ，则 slen 最小为：1

【解析】若t不是s子串（或t==s）输出都为0，但为保证程序执行，最少应输入一个字符。

若 tlen = 10，输出为 $2$ ，则 slen 最小为：12。

输出为$2$说明slen最多连续删除$2$个后为$10$，所以最小为12。

完善程序

（匠人的自我修养）一个匠人决定要学习 $n$ 个新技术，要想成功学习一个新技术，他不仅要拥有一定的经验值，而且还必须要先学会若干个相关的技术。学会一个新技术之后，他的经验值会增加一个对应的值。给定每个技术的学习条件和习得后获得的经验值，给定他已有的经验值，请问他最多能学会多少个新技术。

输入第一行有两个数，分别为新技术个数 $n(1\le n\le 10^3)$，以及已有经验值 $(\le 10^7)$。

接下来 $n$ 行。第 $i$ 行的两个整数，分别表示学习第$i$ 个技术所需的最低经验值 $(\le 10^7)$，以及学会第 $i$ 个技术后可获得的经验值 ($\le 10^4$)。

接下来 $n$ 行。第 $i$ 行的第一个数 $m_i(0\le m_i<n)$，表示第 $i$ 个技术的相关技术数量。紧跟着 $m$ 个两两不同的数，表示第 $i$ 个技术的相关技术编号，输出最多能学会的新技术个数。
下面的程序已 $O(n^2)$的时间复杂完成这个问题，试补全程序。

#include
using namespace std;
const int maxn = 1001;

int n;
int cnt[maxn];
int child [maxn][maxn];
int unlock[maxn];
int threshold[maxn],bonus[maxn];
int points;
bool find(){
     
    int target=-1;
    for (int i = 1;i<=n;++i)
        if(① && ②){
     
            target = i;
            break;
    }
    if(target==-1)
        return false;
    unlock[target]=-1;
    ③
    for (int i=0;i<cnt[target];++i)
        ④
    return true;
}

int main(){
     
    scanf("%d%d",&n, &points);
    for (int i =1; i<=n;++i){
     
        cnt [i]=0;
        scanf("%d%d",&threshold[i],&bonus[i]);
    }
    for (int i=1;i<=n;++i){
     
        int m;
        scanf("%d",&m);
        ⑤
        for (int j=0; j<m ;++j){
     
            int fa;
            scanf("%d", &fa);
            child[fa][cnt[fa]]=i;
            ++cnt[fa];
        }
    }

    int ans = 0;
    while(find())
        ++ans;

    printf("%d", ans);
    return 0;
}

【解析】程序每次都先学习一个已经达到条件但还未学习的技能，学习后更新经验值和其他技能与该技能有关的学习条件，不断重复至没有技能可以学。unlock数组为对应技能需学习的前置技能数，大于$0$说明有前置技能要学，为$-1$表示已学习。

• 空①，unlock[i] == 0表示对应技能需学习的前置技能数为$0$，即第i项技能解锁。
• 空②，要学习第i项技能，除了第i项技能已经解锁，还需要由足够的经验值，即points >= threshold[i]
• 空③，学习了第i项技能，将获得相应的经验值，即points += bonus[target]。
• 空④， 学习了第i项技能，还将解锁以第i项技能为前置条件的其它技能，即unlock[child[target][i]] -= 1
• 空5，初始化第i项技能的前置技能的个数，即unlock[i] = m

2.（取石子）Alice 和 Bob 两个人在玩取石子游戏，他们制定了 $n$ 条取石子的规则，第 $i$ 条规则为：如果剩余的石子个数大于等于 a[i] 且大于等于 b[i]，那么她们可以取走 b[i] 个石子。他们轮流取石子。如果轮到某个人取石子，而她们无法按照任何规则取走石子，那么他就输了，一开始石子有 m 个。请问先取石子的人是否有必胜的方法？

输入第一行有两个正整数，分别为规则个数 $n(1\le n\le 64)$，以及石子个数 $m(\le 10^7)$。

接下来 $n$ 行。第$i$行有两个正整数 $a[i]$ 和 $b[i]$。$1\le a[i]\le 10^7$, $1\le b[i]\le 64$

如果先取石子的人必胜，那么输出“Win”，否则输出“Loss”

提示：
可以使用动态规划解决这个问题。由于 b[i] 不超过 $64$，所以可以使用位无符号整数去压缩必要的状态。

status 是胜负状态的二进制压缩，trans 是状态转移的二进制压缩。

代码说明：

“~”表示二进制补码运算符，它将每个二进制位的 $0$ 变成 $1$、$1$ 变为 $0$；

而“^”表示二进制异或运算符，它将两个参与运算的数重的每个对应的二进制位一一进行比较，若两个二进制位相同，则运算结果的对应二进制位为 $0$，反之为 $1$。

ull 标识符表示它前面的数字是 unsigned long long 类型。

试补全程序。

#include 
#include
using namespace std ;
const int maxn = 64;
int n,m;
int a[maxn], b[maxn];
unsigned long long status, trans;
bool win;
int main() {
     
    scanf("%d%d",&n, &m);
    for (int i = 0; i < n; ++i)
        scanf("%d%d", &a[i], &b[i]);
    for (int  i = 0; i < n; ++i)
         for (int j = i + 1; j < n; ++j)
            if (a[i] > a[j]) {
     
                swap(a[i], a[j]);
                swap(b[i], b[j]);
            }
    status = ①;
    trans = 0;
    for (int i = 1, j = 0; i <= m; ++i) {
     
        while (j < n && ②) {
     
            ③;
            ++j;
        }
        win = ④;
        ⑤;
    }

    puts(win ?  "Win" : "Loss");

    return 0;
}

【解析】使用动态规划的思想解决问题：

• 状态表示：f[i]表示有i个石子时，先手有无必胜的策略。
• 状态转移：若对于i个石子有先手必赢策略，则存在存在规则j$(i\ge a[j],i\ge b[j])$，使得有i - b[j]个石子时，先手必败，即f[i - b[j]] = false。那么状态转移方程：
  $$f[i]=OR(!f[i-b[j]]),i\ge a[j]并且i\ge b[j]$$
• 初始状态：f[0] = 0，表示$0$个石子时，先手必败。

题目给出的策略数和数组b数字都不超过64，所以仅考虑f[i-1]..f[i-64],可将其状态压缩至一个ull整数中。其中status用于记录对于i个石子，i-1..i-64是否有先手必胜策略。

• 空①，初始化status，最开始石子是0个，应该是先手必败的状态，所以最低位不能是1，因此可选status = ~0ull&1。
• 空②，题目实现有将规则按a[i]进行从小到大排序，所以可使用规则只增加不减少。此循环用于增加当前可选的规则，当石子数量i达到规则a[j]时，即可发生状态转移，使用该规则。状态转移到trans变量，因此可选a[j] == i。
• 空③，此行是用来在原有规则上，新增”取b[j]个石子”的规则。二进制新增用|。因此可选trans |= 1ull << (b[j] - 1)
• 空④，计算win的值，先手是否必胜。对当前状态和以前状态做判断。选择：~status & trans。
  -空⑤，更新status状态值，将当前win值记录到status中。status = status << 1 ^ win。