Python-opencv+KNN求解数独
最近一直在玩数独,突发奇想实现图像识别求解数独,输入到输出平均需要0.5s。
整体思路大概就是识别出图中数字生成list,然后求解。
输入输出demo
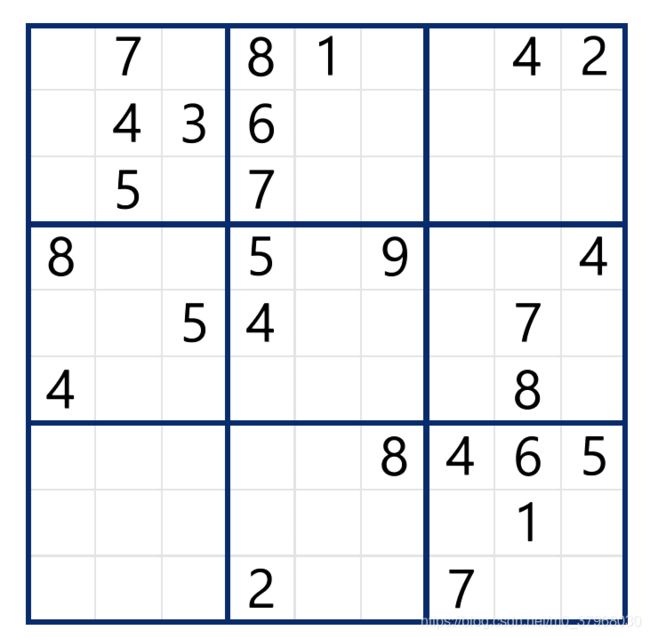
数独采用的是微软自带的Microsoft sudoku软件随便截取的图像,如下图所示:
经过程序求解后,得到的结果如下图所示:
程序具体流程
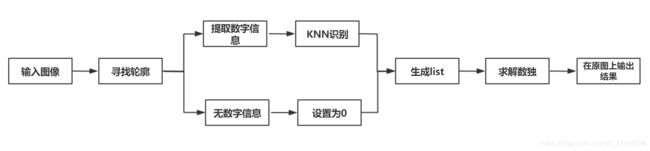
程序整体流程如下图所示:
读入图像后,根据求解轮廓信息找到数字所在位置,以及不包含数字的空白位置,提取数字信息通过KNN识别,识别出数字;无数字信息的在list中置0;生成未求解数独list,之后求解数独,将信息在原图中显示出来。
# -*-coding:utf-8-*-
import os
import cv2 as cv
import numpy as np
import time
####################################################
#寻找数字生成list
def find_dig_(img, train_set):
if img is None:
print("无效的图片!")
os._exit(0)
return
_, thre = cv.threshold(img, 230, 250, cv.THRESH_BINARY_INV)
_, contours, hierarchy = cv.findContours(thre, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
sudoku_list = []
boxes = []
for i in range(len(hierarchy[0])):
if hierarchy[0][i][3] == 0: # 表示父轮廓为 0
boxes.append(hierarchy[0][i])
# 提取数字
nm = []
for j in range(len(boxes)): # 此处len(boxes)=81
if boxes[j][2] != -1:
x, y, w, h = cv.boundingRect(contours[boxes[j][2]])
nm.append([x, y, w, h])
# 在原图中框选各个数字
cropped = img[y:y + h, x:x + w]
im = img_pre(cropped) #预处理
AF = incise(im) #切割数字图像
result = identification(train_set, AF, 7) #knn识别
sudoku_list.insert(0, int(result)) #生成list
else:
sudoku_list.insert(0, 0)
if len(sudoku_list) == 81:
sudoku_list= np.array(sudoku_list)
sudoku_list= sudoku_list.reshape((9, 9))
print("old_sudoku -> \n", sudoku_list)
return sudoku_list, contours, hierarchy
else:
print("无效的图片!")
os._exit(0)
######################################################
#KNN算法识别数字
def img_pre(cropped):
# 预处理数字图像
im = np.array(cropped) # 转化为二维数组
for i in range(im.shape[0]): # 转化为二值矩阵
for j in range(im.shape[1]):
# print(im[i, j])
if im[i, j] != 255:
im[i, j] = 1
else:
im[i, j] = 0
return im
# 提取图片特征
def feature(A):
midx = int(A.shape[1] / 2) + 1
midy = int(A.shape[0] / 2) + 1
A1 = A[0:midy, 0:midx].mean()
A2 = A[midy:A.shape[0], 0:midx].mean()
A3 = A[0:midy, midx:A.shape[1]].mean()
A4 = A[midy:A.shape[0], midx:A.shape[1]].mean()
A5 = A.mean()
AF = [A1, A2, A3, A4, A5]
return AF
# 切割图片并返回每个子图片特征
def incise(im):
# 竖直切割并返回切割的坐标
a = [];
b = []
if any(im[:, 0] == 1):
a.append(0)
for i in range(im.shape[1] - 1):
if all(im[:, i] == 0) and any(im[:, i + 1] == 1):
a.append(i + 1)
elif any(im[:, i] == 1) and all(im[:, i + 1] == 0):
b.append(i + 1)
if any(im[:, im.shape[1] - 1] == 1):
b.append(im.shape[1])
# 水平切割并返回分割图片特征
names = locals();
AF = []
for i in range(len(a)):
names['na%s' % i] = im[:, range(a[i], b[i])]
if any(names['na%s' % i][0, :] == 1):
c = 0
else:
for j in range(names['na%s' % i].shape[0]):
if j < names['na%s' % i].shape[0] - 1:
if all(names['na%s' % i][j, :] == 0) and any(names['na%s' % i][j + 1, :] == 1):
c = j
break
else:
c = j
if any(names['na%s' % i][names['na%s' % i].shape[0] - 1, :] == 1):
d = names['na%s' % i].shape[0] - 1
else:
for j in range(names['na%s' % i].shape[0]):
if j < names['na%s' % i].shape[0] - 1:
if any(names['na%s' % i][j, :] == 1) and all(names['na%s' % i][j + 1, :] == 0):
d = j + 1
break
else:
d = j
names['na%s' % i] = names['na%s' % i][range(c, d), :]
AF.append(feature(names['na%s' % i])) # 提取特征
for j in names['na%s' % i]:
pass
return AF
# 训练已知图片的特征
def training():
train_set = {}
for i in range(9):
value = []
for j in range(15):
ima = cv.imread('E:/test_image/knn_test/{}/{}.png'.format(i + 1, j + 1), 0)
im = img_pre(ima)
AF = incise(im)
value.append(AF[0])
train_set[i + 1] = value
return train_set
# 计算两向量的距离
def distance(v1, v2):
vector1 = np.array(v1)
vector2 = np.array(v2)
Vector = (vector1 - vector2) ** 2
distance = Vector.sum() ** 0.5
return distance
# 用最近邻算法识别单个数字
def knn(train_set, V, k):
key_sort = [11] * k
value_sort = [11] * k
for key in range(1, 10):
for value in train_set[key]:
d = distance(V, value)
for i in range(k):
if d < value_sort[i]:
for j in range(k - 2, i - 1, -1):
key_sort[j + 1] = key_sort[j]
value_sort[j + 1] = value_sort[j]
key_sort[i] = key
value_sort[i] = d
break
max_key_count = -1
key_set = set(key_sort)
for key in key_set:
if max_key_count < key_sort.count(key):
max_key_count = key_sort.count(key)
max_key = key
return max_key
# 生成数字
def identification(train_set, AF, k):
result = ''
for i in AF:
key = knn(train_set, i, k)
result = result + str(key)
return result
######################################################
######################################################
#求解数独
def get_next(m, x, y):
# 获得下一个空白格在数独中的坐标。
:param m 数独矩阵
:param x 空白格行数
:param y 空白格列数
"""
for next_y in range(y + 1, 9): # 下一个空白格和当前格在一行的情况
if m[x][next_y] == 0:
return x, next_y
for next_x in range(x + 1, 9): # 下一个空白格和当前格不在一行的情况
for next_y in range(0, 9):
if m[next_x][next_y] == 0:
return next_x, next_y
return -1, -1 # 若不存在下一个空白格,则返回 -1,-1
def value(m, x, y):
# 返回符合"每个横排和竖排以及九宫格内无相同数字"这个条件的有效值。
i, j = x // 3, y // 3
grid = [m[i * 3 + r][j * 3 + c] for r in range(3) for c in range(3)]
v = set([x for x in range(1, 10)]) - set(grid) - set(m[x]) - \
set(list(zip(*m))[y])
return list(v)
def start_pos(m):
# 返回第一个空白格的位置坐标
for x in range(9):
for y in range(9):
if m[x][y] == 0:
return x, y
return False, False # 若数独已完成,则返回 False, False
def try_sudoku(m, x, y):
# 试着填写数独
for v in value(m, x, y):
m[x][y] = v
next_x, next_y = get_next(m, x, y)
if next_y == -1: # 如果无下一个空白格
return True
else:
end = try_sudoku(m, next_x, next_y) # 递归
if end:
return True
m[x][y] = 0 # 在递归的过程中,如果数独没有解开,
# 则回溯到上一个空白格
def sudoku_so(m):
x, y = start_pos(m)
try_sudoku(m, x, y)
print("new_sudoku -> \n", m)
return m
###################################################
# 将结果绘制到原图
def draw_answer(img, contours, hierarchy, new_sudoku_list ):
new_sudoku_list = new_sudoku_list .flatten().tolist()
for i in range(len(contours)):
cnt = contours[i]
if hierarchy[0, i, -1] == 0:
num = new_soduku_list.pop(-1)
if hierarchy[0, i, 2] == -1:
x, y, w, h = cv.boundingRect(cnt)
cv.putText(img, "%d" % num, (x + 19, y + 56), cv.FONT_HERSHEY_SIMPLEX, 1.8, (0, 0, 255), 2) # 填写数字
cv.imwrite("E:/answer.png", img)
if __name__ == '__main__':
t1 = time.time()
train_set = training()
img = cv.imread('E:/test_image/python_test_img/Sudoku.png')
img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
sudoku_list, contours, hierarchy = find_dig_(img_gray, train_set)
new_sudoku_list = sudoku_so(sudoku_list)
draw_answer(img, contours, hierarchy, new_sudoku_list )
print("time :",time.time()-t1)
PS:
使用KNN算法需要创建训练集,数独中共涉及9个数字,“1,2,3,4,5,6,7,8,9”各15幅图放入文件夹中,如下图所示。
到此这篇关于Python图像识别+KNN求解数独的实现的文章就介绍到这了,更多相关Python KNN求解数独内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!