【数据结构】线性表专题——一元多项式计算器的设计实现

halo~我是bay_Tong桐小白
本文内容是桐小白个人对所学知识进行的总结和分享，知识点会不定期进行编辑更新和完善，了解最近更新内容可参看更新日志，欢迎各位大神留言、指点

本文内容为线性表专题，线性表知识点汇总详细见本栏文章《线性表总结——基本知识要点汇总》

【更新日志】

最近更新：

• 暂时没有编辑记录，后续会持续完善优化

相关知识内容回顾

一元多项式存储设计

• 顺序存储
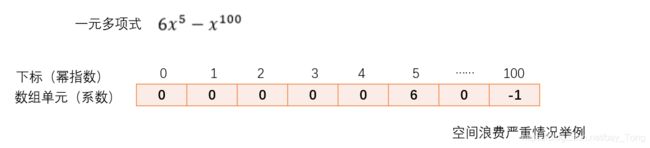
  数组下标表示每一项的幂指数，数组单元内存储每一项的系数
  
  优点：编程简单调试容易
  缺点：需要事先分配一个较大的数组空间，对于幂指数分布差异大的多项式会存在严重的空间浪费问题
  
• 链式存储
  
  优点：动态性强
  缺点：编程相对复杂，调试比较困难

顺序表、单链表的工作原理及增删改查、合并等基本操作
详细见本栏文章《线性表总结——基本知识要点汇总》

任务描述

题目：

输入和输出：
1）输入

• 从键盘输入运算指令（相加、相减、相乘），根据运算指令进行相应运算；
• 从键盘输入两个多项式的系数和指数；
• 系数和指数采用int类型，运算结果不超出int取值范围。

2）输出

• 每种运算结果以多项式形式输出，要输出升幂和降幂两种情况。
• 结果多项式中无重复阶项、无零系数项，输出多项式时请采用如下易读形式（一元多项式，总变元为x）：　x^4 - 3 x^2 + 5

项目要求：

• 实现一个简单的交互式界面，包括系统菜单、输入提示等。
• 多项式运算前首先判定多项式特点，根据多项式是否稀疏来选用合适的存储结构；
• 根据多项式不同的运算要求选择合适的存储结构；
• 上机编辑、调试出完整正确的程序，包括相加、相减、相乘运算。

需求分析

• 需求背景：为掌握顺序表和单链表的存储特点及插入、删除等算法。能够灵活运用顺序表和单链表的相关算法实现一元多项式的计算。
• 需求目的：实验人员知识实践与巩固拔高
• 面向使用者：实验人员及其他用户
• 系统需求：多项式加减乘除、多项式合并、多项式升降幂排序、多项式输出、简易人机交互界面

主要数据类型与变量

typedef struct PolyNode *Polynomial;
struct PolyNode {
     
	int coef;//系数
	int expon;//指数
	Polynomial link;//后继指针
};

算法或程序模块

算法相关设计

• 在多项式输入完成以及多项式运算完成后，均会执行合并同类项以及升幂排序的操作，以消除多项式中的重复阶项以及零系数项
• 多项式减法可以通过Rev函数将被减多项式的每一项系数取相反数后再执行Add操作来实现（除法同理可进行每一项系数求倒数后执行Mult，本文暂未实现，后续持续更新）
• 由于在多项式输入完成以及多项式运算完成后，均执行了合并同类项以及升幂排序的操作，因此升幂输出即按顺序遍历多项式链表并输出，降幂输出可采用递归的思想进行实现

void display();//交互界面
void testIO();//多项式输入输出测试
void calculate();//多项式计算
void information();//相关说明
void Attach(int c, int e, Polynomial *pRear);//向多项式链表中插入结点
Polynomial ReadPoly();//读取多项式链表
Polynomial Add(Polynomial P1, Polynomial P2);//多项式相加
Polynomial Mult(Polynomial P1, Polynomial P2);//多项式相乘
Polynomial Combin(Polynomial P);//合并同类项
Polynomial Up(Polynomial L);//多项式升幂排序
Polynomial Rev(Polynomial P);//多项式每一项系数取相反数
void PrintUp(Polynomial P);//升幂输出
void PrintDown(Polynomial P, int flag);//降幂输出

测试方案设计

代码实现（C语言）

#include
#include
typedef struct PolyNode *Polynomial;
struct PolyNode {
     
	int coef;//系数
	int expon;//指数
	Polynomial link;//后继指针
};

void display();//交互界面
void testIO();//多项式输入输出测试
void calculate();//多项式计算
void information();//相关说明
void Attach(int c, int e, Polynomial *pRear);//向多项式链表中插入结点
Polynomial ReadPoly();//读取多项式链表
Polynomial Add(Polynomial P1, Polynomial P2);//多项式相加
Polynomial Mult(Polynomial P1, Polynomial P2);//多项式相乘
Polynomial Combin(Polynomial P);//合并同类项
Polynomial Up(Polynomial L);//多项式升幂排序
Polynomial Rev(Polynomial P);//多项式每一项系数取相反数
void PrintUp(Polynomial P);//升幂输出
void PrintDown(Polynomial P, int flag);//降幂输出

int main() {
     
	int option;
	while (1) {
     
		system("cls");	display();
		scanf("%d", &option);	getchar(); fflush(stdin);
		switch (option) {
     
		case 1:		testIO();		break;//多项式输入输出测试
		case 2:		calculate();	break;//多项式计算
		case 3:		information();	break;//相关说明
		case 4:		return 0;//退出程序
		default:	printf("输入有误，请重新输入\n");
			system("pause");	break;
		}
	}
}
//交互界面
void display() {
     
	printf("**************一元多项式计算器**************\n");
	printf("1.多项式输入输出测试\n");
	printf("2.多项式计算\n");
	printf("3.相关说明\n");
	printf("4.退出程序\n");
	printf("请输入您的选择：");
}
//多项式输入输出测试
void testIO() {
     
	printf("多项式输入输出测试:\n");
	Polynomial L = ReadPoly();//读入多项式
	PrintUp(L);//升序输出
	PrintDown(L, 0);//降序输出
	printf("测试完毕\n");	system("pause");
}
//多项式计算
void calculate() {
     
	Polynomial P1, P2, Res;
	char flag;	int option;
	printf("多项式计算:\n");
	while (1) {
     
		printf("请输入运算符号(仅支持+、-、*,输入#返回上一层)：");
		scanf("%c", &flag);	getchar();	fflush(stdin);
		switch (flag) {
     
		case '+':	option = 1;	break;
		case '-':	option = 2;	break;
		case '*':	option = 3;	break;
		case '#':	return;
		default:	printf("输入有误，请重新输入\n");
			system("pause");	option = -1; break;
		}
		if (option != -1) {
     
			P1 = ReadPoly();	getchar();	fflush(stdin);
			P2 = ReadPoly();	getchar();	fflush(stdin);
			if (option == 1) {
      Res = Add(P1, P2); }
			else if (option == 2) {
      Res = Add(P1, Rev(P2)); }
			else if (option == 3) {
      Res = Mult(P1, P2); }
			PrintUp(Res);	PrintDown(Res, 0);	system("pause");
		}
	}
}
//相关说明
void information() {
     
	printf("相关说明：\n");
	printf("--------------------实验一_一元多项式计算器\n");
	printf("主要功能：多项式相加、相减、相乘\n");
	printf("课程名称：数据结构\n");
	system("pause");
}
//向多项式链表中插入结点（尾插法）
void Attach(int c, int e, Polynomial *pRear) {
     
	Polynomial P;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	if (c == 0) {
      return; }
	else {
      P->coef = c;	P->expon = e; }
	P->link = NULL;	(*pRear)->link = P;		*pRear = P;
}
//读取多项式链表
Polynomial ReadPoly() {
     
	Polynomial P, Rear, t;
	int n, c, e;
	printf("输入多项式的项数：");
	scanf("%d", &n);
	if (n <= 0) {
      printf("输入有误\n"); return NULL; }
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->link = NULL;	Rear = P;
	printf("输入多项式的系数与指数：\n");
	while (n--) {
     
		scanf("%d%d", &c, &e);
		Attach(c, e, &Rear);
	}
	t = P; P = P->link; free(t);
	P = Combin(P);
	return P;
}
//多项式相加
Polynomial Add(Polynomial P1, Polynomial P2)
{
     
	Polynomial P, Rear, t;
	Polynomial t1 = P1;
	Polynomial t2 = P2;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->link = NULL;	Rear = P;
	while (t1&&t2)
	{
     
		if (t1->expon == t2->expon)
		{
     
			if (t1->coef + t2->coef)
			{
     
				Attach(t1->coef + t2->coef, t1->expon, &Rear);
				t1 = t1->link;	t2 = t2->link;
			}
		}
		else if (t1->expon > t2->expon)
		{
     
			Attach(t1->coef, t1->expon, &Rear);
			t1 = t1->link;
		}
		else
		{
     
			Attach(t2->coef, t2->expon, &Rear);
			t2 = t2->link;
		}
	}
	while (t1)
	{
     
		Attach(t1->coef, t1->expon, &Rear);
		t1 = t1->link;
	}
	while (t2)
	{
     
		Attach(t2->coef, t2->expon, &Rear);
		t2 = t2->link;
	}
	Rear->link = NULL;
	t = P;	P = P->link;	free(t);
	P = Combin(P);
	return P;
}
//多项式相乘
Polynomial Mult(Polynomial P1, Polynomial P2) {
     
	Polynomial P, Rear, t1, t2, t;
	int c, e;
	if (!P1 || !P2)return NULL;
	t1 = P1; t2 = P2;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->link = NULL;	Rear = P;
	while (t2) {
     
		Attach(t1->coef*t2->coef, t1->expon + t2->expon, &Rear);
		t2 = t2->link;
	}
	t1 = t1->link;
	while (t1) {
     
		t2 = P2; Rear = P;
		while (t2) {
     
			e = t1->expon + t2->expon;
			c = t1->coef*t2->coef;
			while (Rear->link&&Rear->link->expon > e) {
     
				Rear = Rear->link;
			}
			if (Rear->link&&Rear->link->expon == e) {
     
				if (Rear->link->coef + c) {
     
					Rear->link->coef += c;
				}
				else {
     
					t = Rear->link;
					Rear->link = t->link;
					free(t);
				}
			}
			else {
     
				t = (Polynomial)malloc(sizeof(struct PolyNode));
				t->coef = c; t->expon = e;
				t->link = Rear->link;
				Rear->link = t; Rear = Rear->link;
			}
			t2 = t2->link;
		}
		t1 = t1->link;
	}
	t2 = P; P = P->link; free(t2);
	P = Combin(P);
	return P;
}
//合并同类项
Polynomial Combin(Polynomial L) {
     
	Polynomial Head = L;
	Polynomial P;
	Polynomial Pr = L;
	if (!L) {
     
		P = (Polynomial)malloc(sizeof(struct PolyNode));
		P->coef = 0;	P->expon = 0;	P->link = NULL;
		return L;
	}
	P = L->link;
	while (Head) {
     
		while (P) {
     
			if (P->expon == Head->expon) {
     
				Head->coef = Head->coef + P->coef;
				if (Head->coef == 0) {
      Head->expon = 0; }
				Pr->link = P->link; free(P); P = Pr->link;
			}
			else {
     
				Pr = Pr->link;	P = Pr->link;
			}
		}
		Head = Head->link;	Pr = Head;
		if (Head)P = Head->link;
	}
	L = Up(L);
	return L;
}
//多项式升幂
Polynomial Up(Polynomial L) {
     
	Polynomial Head = (Polynomial)calloc(1, sizeof(struct PolyNode));
	Polynomial P = L, node = Head, t = Head;
	if (!P || !Head) {
      printf("NULL\n"); return NULL; }
	L = L->link;	P->link = node->link;	node->link = P;
	P = L;
	while (P) {
     
		node = Head;
		while (node) {
     
			if (node->link == NULL || (P->expon < node->link->expon)) {
     
				L = L->link;
				P->link = node->link;	node->link = P;
				break;
			}
			else {
      node = node->link; }
		}
		P = L;
	}
	Head = Head->link; free(t);
	return Head;
}
//多项式每一项系数取相反数
Polynomial Rev(Polynomial P) {
     
	Polynomial node = P;
	if (!P) {
      return NULL; }
	while (node) {
     
		node->coef = -(node->coef);
		node = node->link;
	}
	return P;
}
//升幂输出
void PrintUp(Polynomial P) {
     
	int flag = 0;
	printf("结果如下(升幂)：");
	if (!P) {
      printf("0\n"); return; }
	while (P) {
     
		if (!flag) {
      flag = 1; }
		else
			if (P->coef >= 0) {
      printf("+"); }

		if (P->expon == 0) {
      printf("%d", P->coef); }
		else {
      printf("%dx^%d", P->coef, P->expon); }
		P = P->link;
	}
	printf("\n");
}
//降幂输出
void PrintDown(Polynomial P, int flag) {
     
	if (flag == 0) {
      printf("结果如下(降幂)："); }
	if (!P) {
      printf("0\n"); return; }
	if (P->link) {
      PrintDown(P->link, 1); }
	if (P->coef >= 0 && P->link != NULL) {
      printf("+"); }
	if (P->coef == 0 || P->expon == 0) {
      printf("%d", P->coef); }
	else {
      printf("%dx^%d", P->coef, P->expon); }
	if (flag == 0) {
      printf("\n"); }
}

持续更新中……
我是桐小白，一个摸爬滚打的计算机小白