【机器人学与计算机视觉基础】(一)位置与姿态描述 1 位姿的抽象符号表示
位置与姿态描述
1 位姿的抽象符号表示
提示:在本文中,我们会用到这几个抽象的符号:“ ξ \xi ξ”、“·”和“ ⊕ \oplus ⊕”。读者只需知道它们的作用就行,在后续文章会将其转化为MATLAB中实现的标准的数学对象和运算符。
机器人和计算机视觉中的一个基本要求是能够表示物体在环境中的位置和方向。这些物体包括机器人、摄像机、工件、障碍物和路径。
空间中的点可以被描述为一个坐标向量,也被称为一个约束向量。如下图所示,点 P P P由一个相对于绝对坐标系的坐标向量表示。

而对于空间中的物体,我们表示它时并不仅仅描述其上单独的点,而是用该物体坐标系的位置和方向来描述。坐标系的位置和方向总称为位姿,图形上用一组坐标轴表示。相对于一个参考坐标系的某个坐标系的相对位姿用符号 ξ \xi ξ表示。
更多时候我们需要考虑组成物体的一组点。我们认为物体是刚性的,构成它的点相对于物体坐标系保持固定的相对位置,如下图所示。

在上图中
-
小车坐标系用 { B } \{B\} { B}标记,由一个相对位姿 ξ B \xi_B ξB(如果没有初始上标,我们默认位姿的变化是相对于用 { О } \{О\} { О}表示的世界坐标系的,即 O ξ B ^O\xi_B OξB)表示(细的黑色箭头)。
-
坐标系 { B } \{B\} { B}的坐标以坐标系的标记作为其下标,用 x B x_B xB和 y B y_B yB表示。(粗的红色箭头表示)
-
组成小车的点用相对于坐标系 { B } \{B\} { B}的向量表示(细的红色箭头)。
下图显示了两个坐标系 { A } \{A\} { A}、 { B } \{B\} { B},以及 { B } \{B\} { B}相对于 { A } \{A\} { A}的相对位姿 A ξ B ^A\xi_B AξB。前面的上标表示参考坐标系,下标表示被描述的坐标系。
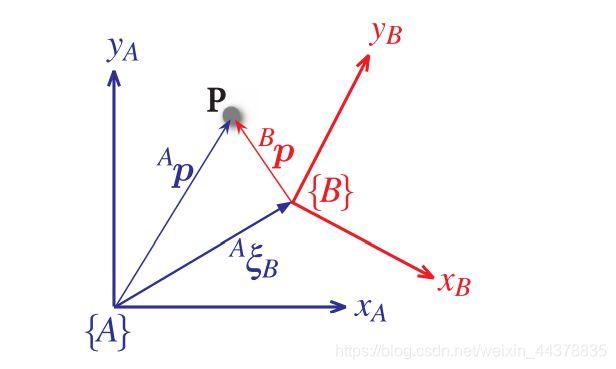
我们也可以认为 A ξ B ^A\xi_B AξB描述了一组动作——对 { A } \{A\} { A}施加平移和旋转使它转化为 { B } \{B\} { B}。
在上图中的 P P P点可用 { A } \{A\} { A}, { B } \{B\} { B}任何一个坐标系表示(坐标系 { B } \{B\} { B}相对于坐标系 { A } \{A\} { A}的位姿记作 A ξ B ^A\xi_B AξB)。用式子表示为:
A p = A ξ B ⋅ B p ^Ap=^A\xi_B\cdot^Bp Ap=AξB⋅Bp
等式右侧表示从 { A } \{A\} { A}到 { B } \{B\} { B}然后到 P P P的动作。运算符“ ⋅ · ⋅”将一个向量转换为一个新的向量,它们是用一个不同的坐标系来描述的相同点。
相对位姿一个重要的特点是它们可以被合成或组合。以下图情况为例,
如果一个坐标系可以被其他坐标系用相对位姿描述,那么它们的关系可以记为
A ξ C = A ξ B ⊕ B ξ C ^A\xi_C=^A\xi_B\oplus^B\xi_C AξC=AξB⊕BξC
用语言可以表述为, { C } \{C\} { C}相对于 { A } \{A\} { A}的位姿可由 { B } \{B\} { B}相对于 { A } \{A\} { A}的位姿和 { C } \{C\} { C}相对于 { B } \{B\} { B}的位姿合成得到。我们利用运算符“ ⊕ \oplus ⊕”表示相对位姿的合成。
在这种情况下点 P P P可以用相对于坐标系 { A } \{A\} { A}, { B } \{B\} { B}或 { C } \{C\} { C}的坐标向量表示。这些坐标系用相对位姿描述:
A p = ( A ξ B ⊕ B ξ C ) ⋅ C p ^Ap=(^A\xi_B\oplus^B\xi_C)\cdot^Cp Ap=(AξB⊕BξC)⋅Cp
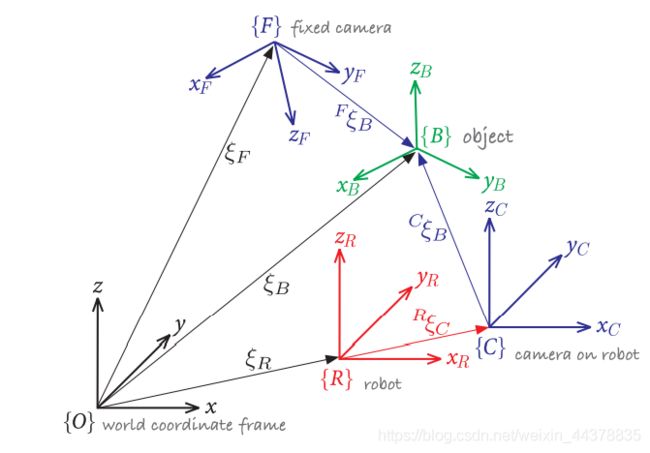
在前面的例子中主要讨论了二维坐标系的情况,能适用于一大类机器人的问题,特别是在平面世界里作业的移动机器人。对于其他问题,我们需要用三维坐标系来表示三维世界中的物体,如飞行机器人、水下机器人的位姿或者机器人手臂夹持的工具末端。
其中每个实体上都固接了一个三维坐标系,并表示出了它们之间的相对位姿。固定摄像头从固定的视角观察物体,并估计物体相对于摄像头本身的位姿。另一个摄像头是不固定的,它固接到机器人上,与机器人有固定的相对位姿,并估计出物体相对于该摄像头的位姿。
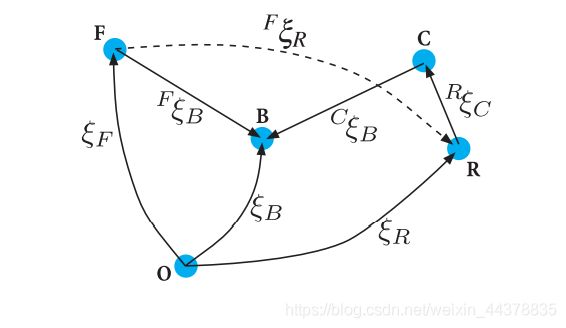
图中的每个节点代表一个位姿,每条边代表一个相对位姿。从 X X X到 Y Y Y的箭头记作 X ξ Y ^X\xi_Y XξY,表示 Y Y Y相对于 X X X的位姿。前面我们提到过可以用运算符 ⊕ \oplus ⊕来复合成相对位姿,这里可以用它写出一些空间关系:
ξ F ⊕ F ξ B = ξ R ⊕ R ξ C ⊕ C ξ B ξ F ⊕ F ξ R = 0 ξ R \begin{array}{l}\xi_{F} \oplus^{F} \xi_{B}=\xi_{R} \oplus^{R} \xi_{C} \oplus{ }^{C} \xi_{B} \\\xi_{F} \oplus^{F} \xi_{R}={ }^{0} \xi_{R}\end{array} ξF⊕FξB=ξR⊕RξC⊕CξBξF⊕FξR=0ξR
每个方程表示了图中的一个闭环。方程等号两侧的每一边各表示一条网络的通路,即一组按照从头到尾顺序连接的边(箭头线)。等式两边的起始节点和结束节点必须相同。
位姿表示的一个非常有用的属性是其代数运算能力。以上面第二个闭环方程为例,
ξ F ⊕ F ξ R = 0 ξ R \xi_{F} \oplus^{F} \xi_{R}={ }^{0} \xi_{R} ξF⊕FξR=0ξR
它表示机器人的位姿等同于两个相对位姿的合成:从世界坐标系 { O } \{O\} { O}到固定摄像机坐标系 { F } \{F\} { F}的相对位姿,以及从固定摄像机 { F } \{F\} { F}到机器人 { R } \{R\} { R}的相对位姿。
我们可以通过在等式两边同时加上一个逆来消除,,记作
⊖ ξ F ⊕ ξ F ⊕ F ξ R = ⊖ ξ F ⊕ ξ R F ξ R = ⊖ ξ F ⊕ ξ R \begin{aligned}\ominus \xi_{F} \oplus \xi_{F} \oplus^{F} \xi_{R} &=\ominus \xi_{F} \oplus \xi_{R} \\{ }^{F} \xi_{R} &=\ominus \xi_{F} \oplus \xi_{R}\end{aligned} ⊖ξF⊕ξF⊕FξRFξR=⊖ξF⊕ξR=⊖ξF⊕ξR
其结果就是机器人 { R } \{R\} { R}相对于固定摄像机 { F } \{F\} { F}的位姿。
下面是几个代数运算规则:
ξ ⊕ 0 = ξ , ξ ⊖ 0 = ξ ξ ⊖ ξ = 0 , ⊖ ξ ⊕ ξ = 0 \begin{array}{l}\xi \oplus 0=\xi, \xi \ominus 0=\xi \\\xi \ominus \xi=0, \ominus \xi \oplus \xi=0\end{array} ξ⊕0=ξ,ξ⊖0=ξξ⊖ξ=0,⊖ξ⊕ξ=0
其中0表示一个零相对位姿。一个位姿可以有逆位姿:
⊖ X ξ Y = Y ξ X \ominus^{X} \xi_{Y}={ }^{Y} \xi_{X} ⊖XξY=YξX
该逆位姿在图中可表示为从 Y Y Y到 X X X的一条箭头线。相对位姿可以被复合或合成:
X ξ Y ⊕ Y ξ Z = X ξ Z { }^{X} \xi_{Y} \oplus{ }^{Y} \xi_{Z}={ }^{X} \xi_{Z} XξY⊕YξZ=XξZ
需要注意的是位姿的代数运算规则不同于一般的代数运算规则,位姿复合运算中各个项的位置不能交换:
ξ 1 ⊕ ξ 2 ≠ ξ 2 ⊕ ξ 1 \xi_{1} \oplus \xi_{2} \neq \xi_{2} \oplus \xi_{1} ξ1⊕ξ2=ξ2⊕ξ1
ξ 1 ⊕ ξ 2 = 0 \xi_{1} \oplus \xi_{2}=0 ξ1⊕ξ2=0时才可以互换位置。可以用相对位姿将一个点从一个坐标系中的一个向量转换为另一个坐标系中的另一个向量:
X p = X ξ Y ⋅ Y p { }^{X} \boldsymbol{p}={ }^{X} \xi_{Y} \cdot{ }^{Y} \boldsymbol{p} Xp=XξY⋅Yp
那么, ξ \xi ξ是什么,才可以支持上述代数运算,并适用于我们身边常见的二维或三维的的问题?
在后续的文章中我们将讨论一些对象,其中包括向量以及一些更奇特的数学对象,如齐次变换矩阵、正交旋转矩阵和四元数等。这些数学对象都可以支持上述代数运算,并且非常适合MATLAB的数学编程环境!
参考:
[1] 机器人学、机器视觉与控制:MATLAB算法基础;Peter Corke 著; 刘荣等译.
[2] Robotics,Vision and Control Fundamental Algorithms in MATLAB;Peter Corke
THE END.
感谢阅读。