数据结构与算法 基础实验

实验一 线性表的创建、销毁、插入、删除、遍历等操作的实现：两个有序链表序列的合并

一、 题目

7-1 两个有序链表序列的合并

    已知两个非降序链表序列S1与S2，设计函数构造出S1与S2合并后的新的非降序链表S3。
输入格式:
    输入分两行，分别在每行给出由若干个正整数构成的非降序序列，用−1表示序列的结尾（−1不属于这个序列）。数字用空格间隔。
输出格式:
    在一行中输出合并后新的非降序链表，数字间用空格分开，结尾不能有多余空格；若新链表为空，输出NULL。

二、 解题思路

    考察链表的基础操作，链表为有序链表，需要定义一个结构体来实现链表数据结构，读入链表后比较当前指针所指的两个结点的值，将小的插入新的链表，指针指向下一个元素，重复上述操作即可。

三、 程序设计

声明三个链表并开辟空间
定义指针p，指向第一个链表第一个结点
定义指针q，指向第二个链表第一个结点
while (p，q都不为NULL) {
     
    if（p指向的值大于q指向的值）
        将q指向的值插入第三个链表
        q指向下一个结点
    else
        将p指向的值插入第三个链表
        p指向下一个结点
}
输出第三个链表

四、 程序详解及运行结果

#include
using namespace std;
struct LNode {
     
    int val;
    LNode* next = NULL;
};
int main() {
     
    LNode* L1;
    L1 = (LNode*)malloc(sizeof(LNode));
    LNode* L2;
    L2 = (LNode*)malloc(sizeof(LNode));
    LNode* L3;
    L3 = (LNode*)malloc(sizeof(LNode));
    int temp;
    cin >> temp;
    LNode* l1 = L1;
    while (temp != -1) {
     
        l1->next = (LNode*)malloc(sizeof(LNode));//每次都要开辟空间
        l1 = l1->next;
        l1->val = temp;
        l1->next = NULL;
        cin >> temp;
    }
    cin >> temp;
    LNode* l2 = L2;
    while (temp != -1) {
     
        l2->next = (LNode*)malloc(sizeof(LNode));
        l2 = l2->next;
        l2->val = temp;
        l2->next = NULL;
        cin >> temp;
    }
    LNode* l3 = L3;
    L1 = L1->next;
    L2 = L2->next;
    while (L1 && L2)
    {
     
        if (L1->val <= L2->val) {
     
            l3->next = (LNode*)malloc(sizeof(LNode));
            l3 = l3->next;
            l3->val=L1->val;
            l3->next = NULL;
            L1 = L1->next;
        }
        else {
     
            l3->next = (LNode*)malloc(sizeof(LNode));
            l3 = l3->next;
            l3->val = L2->val;
            l3->next = NULL;
            L2 = L2->next;
        }
    }
    if (L2==NULL) {
     
        while (L1!=NULL) {
     
            l3->next = (LNode*)malloc(sizeof(LNode));
            l3 = l3->next;
            l3->val = L1->val;
            l3->next = NULL;
            L1 = L1->next;
        }
    }
    else {
     
        while (L2!=NULL) {
     
            l3->next = (LNode*)malloc(sizeof(LNode));
            l3 = l3->next;
            l3->val = L2->val;
            l3->next = NULL;
            L2 = L2->next;
        }
    }
    if (L3==NULL) {
     
        cout << "NULL" << endl;
    }
    else {
     
        L3 = L3->next;
        cout << L3->val;
        L3 = L3->next;
        while (L3!=NULL) {
     
            cout << " " << L3->val;
            L3 = L3->next;
        }
        cout << endl;

    }
    return 0;
}

五、 问题及解决过程

    指针每次指向下一个节点之前，都要先开辟空间再访问，并且每次要将next成员赋值成NULL，以方便后续操作。

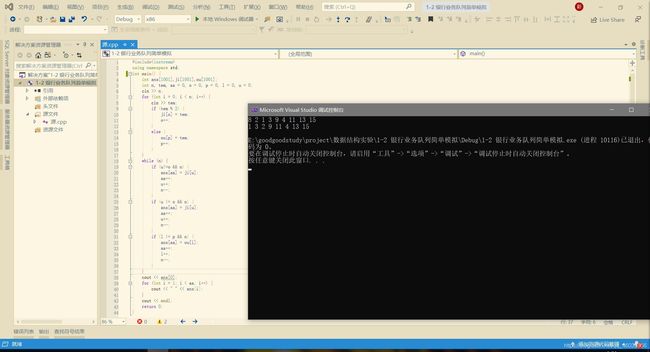
实验二 队列类的实现与测试 ：银行业务队列简单模拟

一、 题目

7-2 银行业务队列简单模拟

    设某银行有A、B两个业务窗口，且处理业务的速度不一样，其中A窗口处理速度是B窗口的2倍 —— 即当A窗口每处理完2个顾客时，B窗口处理完1个顾客。给定到达银行的顾客序列，请按业务完成的顺序输出顾客序列。假定不考虑顾客先后到达的时间间隔，并且当不同窗口同时处理完2个顾客时，A窗口顾客优先输出。
输入格式:
    输入为一行正整数，其中第1个数字N(≤1000)为顾客总数，后面跟着N位顾客的编号。编号为奇数的顾客需要到A窗口办理业务，为偶数的顾客则去B窗口。数字间以空格分隔。
输出格式:
    按业务处理完成的顺序输出顾客的编号。数字间以空格分隔，但最后一个编号后不能有多余的空格。

二、 解题思路

    考察队列的相关基础操作。用线性表模拟队列来实现队列的相关操作即可。

三、 程序设计

声明三个数组
while(数据数量--){
     
    if(为奇数)
        放入第一个数组
    if(为偶数)
        放入第二个数组
}
while(第一个数组和第二个数组均不为空){
     
    第一个数组->第三个数组
    第一个数组->第三个数组
    第二个数组->第三个数组
}
if(第一个数组先空)
    第二个数组剩余元素->第三个数组
else
    第一个数组剩余元素->第三个数组
输出第三个数组

四、 程序详解及运行结果

#include
using namespace std;
int main() {
     
    int ans[1001],ji[1001],ou[1001];
    int n, tem, aa = 0, o = 0, p = 0, l = 0, u = 0;
    cin >> n;
    for (int i = 0; i < n; i++) {
     
        cin >> tem;
        if (tem % 2) {
     
            ji[o] = tem;
            o++;
        }
        else {
     
            ou[p] = tem;
            p++;
        }
    }
    while (n) {
     
        if (u!=o && n) {
     
            ans[aa] = ji[u];
            aa++;
            u++;
            n--;
        }
        if (u != o && n) {
     
            ans[aa] = ji[u];
            aa++;
            u++;
            n--;
        }
        if (l != p && n) {
     
            ans[aa] = ou[l];
            aa++;
            l++;
            n--;
        }
    }
    cout << ans[0];
    for (int i = 1; i < aa; i++) {
     
        cout << " " << ans[i];
    }
    cout << endl;
    return 0;
}

五、 问题及解决过程

    每个线性表定义两个下标表示队首、队尾，通过下标的移动来模拟出队，入队操作。

实验三 栈与队列的应用 ：迷宫寻路

一、 题目

7-1 迷宫寻路

    给定一个M行N列的迷宫图，其中 "0"表示可通路，"1"表示障碍物，无法通行。在迷宫中只允许在水平或上下四个方向的通路上行走，走过的位置不能重复走。
    5行8列的迷宫如下：

1. 0 1 1 1 0 0 0 0
2. 0 0 0 1 0 0 0 0
3. 0 1 0 0 0 1 0 0
4. 0 1 1 1 0 1 1 0
5. 1 0 0 0 0 0 0 0

    则从左上角（1，1）至右下角（5，8）的最短路径为：

1,1--> 2,1--> 2,2--> 2,3--> 3,3 --> 3,4--> 3,5--> 4,5--> 5,5--> 5,6--> 5,7--> 5,8  

    题目保证每个迷宫最多只有一条最短路径。
    请输出该条最短路径，如果不存在任何通路，则输出"NO FOUND".

输入格式:
    第一行，输入M和N值，表示迷宫行数和列数。接着输入M行数值，其中，0表示通路，1表示障碍物。每列数值用空格符间隔。接下来可能输入多组迷宫数据。当输入M的值为-1时结束输入。
输出格式:
    按行顺序输出路径的每个位置的行数和列数，如 x,y。如果不存在任何路径，则输出"NO FOUND".每组迷宫寻路结果用换行符间隔。

二、 解题思路

    考察运用队列进行广度优先搜索。（也可以用栈进行深度优先搜索求解）

三、 程序设计

定义一个队列
将起点加入队列
while(1)
	将当前队列中所有节点向四周的可达节点扩散
	记录每一个扩散节点和到达该顶点的步数
	if(队列为空)
		返回找不到
	if(达到终点)
		退出循环
通过记录的步数找出路径
输出路径
返回找到了

四、 程序详解及运行结果

#include 
#include 
#include 
#include
using namespace std;

struct Position{
     
	int row;
	int col;
};
Position fx[4];

bool findpath(vector<vector<int>>MG, int row, int col){
     
	fx[0].row = 0; fx[0].col = 1;
	fx[1].row = 1; fx[1].col = 0;
	fx[2].row = 0; fx[2].col = -1;
	fx[3].row = -1; fx[3].col = 0;
	for (int i = 0; i < row + 2; i++){
     
		MG[i][col + 1] = 1;
		MG[i][0] = 1;
	}//边界标成 1
	for (int i = 0; i < col + 2; i++){
     
		MG[0][i] = 1;
		MG[row + 1][i] = 1;
	}//边界标成 1
	MG[1][1] = 2;
	queue<Position> road;//用于广搜的队列
	Position next;
	Position here;
	here.col = 1; here.row = 1;
	while (1){
     
		for (int i = 0; i < 4; i++){
     
			next.row = here.row + fx[i].row;
			next.col = here.col + fx[i].col;
			if (MG[next.row][next.col] == 0){
     
				MG[next.row][next.col] = MG[here.row][here.col] + 1;//记录到每一个顶点的步数
				if ((next.row == row) && (next.col == col))
					break;
				road.push(next);
			}
		}
		if ((next.row == row) && (next.col == col))
			break;
		if (road.empty())
			return false;
		here = road.front();
		road.pop();
	}
	int far = MG[row][col] - 2;
	vector<Position>path(far);
	here.row = row;
	here.col = col;
	for (int i = far - 1; i >= 0; i--){
     
		path[i] = here;
		for (int j = 0; j < 4; j++){
     
			next.row = here.row + fx[j].row;
			next.col = here.col + fx[j].col;
			if (MG[next.row][next.col] == i + 2)
				break;
		}
		here = next;
	}
	cout << "1,1" << endl;
	for (int i = 0; i < far; i++)
		cout << path[i].row << "," << path[i].col << endl;
	return true;
}
int main(){
     
	int a, b;
	cin >> a >> b;
	
	vector<vector<int>>mg(a + 2, vector<int>(b + 2));
	while (a != -1 && b != -1){
     
		for (int i = 1; i < a + 1; i++)
			for (int j = 1; j < b + 1; j++)
				cin >> mg[i][j];
		if (findpath(mg, a, b))
			cout << endl;
		else
			cout << "NO FOUND" << endl;
		cin >> a >> b;
	}
}

五、 问题及解决过程

    输出路径是该题难点，这里我通过标记到达每一个顶点的步数从终点一步步往回找前驱节点存储到数组中，再进行输出。

实验四 树的存储结构 ：树的遍历

一、 题目

7-2 树的遍历

    给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。
输入格式:
    输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。
输出格式:
    在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

二、 解题思路

    主要考察树的遍历方法。先通过中序遍历序列和后序遍历序列将树构造出来，然后再输出层序遍历结果。

三、 程序设计

声明树的结点结构体
先通过后序遍历序列找到跟结点
再结合中序遍历将树构架出来
声明三个变量标记中序遍历序列与后序遍历序列遍历的当前位置
用递归函数造树
    if (中序序列遍历完毕)
        返回NULL
    声明一个结点
    将后序序列最后一个值赋给当前结点
    r->val = a[end_hou];
    在中序序列中找到该结点的值所处位置
    在该结点值所处位置左右分别递归该构造树的函数
最后利用广度优先搜索将树层序遍历

四、 程序详解及运行结果

#include 
#include
#include

using namespace std;
typedef struct node {
     
    int val;
    struct node* left;
    struct node* right;
}node, * tree;
vector<int>ans;
vector<int>b(31);
vector<int>a(31);
queue<tree> c;
tree Du(int end_hou, int begin_zhong, int end_zhong) {
     
    if (begin_zhong == end_zhong)
        return NULL;
    tree r = new node();
    r->val = a[end_hou];
    int i, t = a[end_hou];
    for (i = begin_zhong; i < end_zhong; ++i)
        if (t == b[i]) 
            break;
    r->left = Du(end_hou - (end_zhong - i), begin_zhong, i);
    r->right = Du(end_hou - 1, i + 1, end_zhong);
    return r;
}
int main() {
     
    int n, x;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
     
        cin >> a[i];
    }
    int tem;
    for (int i = 1; i <= n; ++i) {
     
        cin >> b[i];
    }
    tree root = Du(n, 1, n + 1);
    if (root)
        c.push(root);
    while (!c.empty())
    {
     
        int n = c.size();
        for (int i = 0; i < n; i++)
        {
     
            tree tem = c.front();
            c.pop();
            ans.push_back(tem->val);
            if (tem->left)
                c.push(tem->left);
            if (tem->right)
                c.push(tem->right);
        }
    }
    cout << ans[0];
    for (int i = 1; i < ans.size(); ++i) {
     
        cout << " " << ans[i];
    }
    return 0;
}

五、 问题及解决过程

    该题最难的部分是利用中序后序序列对树进行还原，需熟记树的遍历方法及其相应遍历结果，找到方法后再进行还原。

实验五 哈夫曼编码 ：哈夫曼编码

一、 题目

7-1 哈夫曼编码

    给定一段文字，如果我们统计出字母出现的频率，是可以根据哈夫曼算法给出一套编码，使得用此编码压缩原文可以得到最短的编码总长。然而哈夫曼编码并不是唯一的。例如对字符串"aaaxuaxz"，容易得到字母 ‘a’、‘x’、‘u’、‘z’ 的出现频率对应为 4、2、1、1。我们可以设计编码 {‘a’=0, ‘x’=10, ‘u’=110, ‘z’=111}，也可以用另一套 {‘a’=1, ‘x’=01, ‘u’=001, ‘z’=000}，还可以用 {‘a’=0, ‘x’=11, ‘u’=100, ‘z’=101}，三套编码都可以把原文压缩到 14 个字节。但是 {‘a’=0, ‘x’=01, ‘u’=011, ‘z’=001} 就不是哈夫曼编码，因为用这套编码压缩得到 00001011001001 后，解码的结果不唯一，“aaaxuaxz” 和 “aazuaxax” 都可以对应解码的结果。本题就请你判断任一套编码是否哈夫曼编码。
输入格式:
    首先第一行给出一个正整数 N（2≤N≤63），随后第二行给出 N 个不重复的字符及其出现频率，格式如下：

c[1] f[1] c[2] f[2] ... c[N] f[N]

    其中c[i]是集合{‘0’ - ‘9’, ‘a’ - ‘z’, ‘A’ - ‘Z’, ‘_’}中的字符；f[i]是c[i]的出现频率，为不超过 1000 的整数。再下一行给出一个正整数 M（≤1000），随后是 M 套待检的编码。每套编码占 N 行，格式为：

c[i] code[i]

    其中c[i]是第i个字符；code[i]是不超过63个’0’和’1’的非空字符串。

输出格式:
    对每套待检编码，如果是正确的哈夫曼编码，就在一行中输出"Yes"，否则输出"No"。
    注意：最优编码并不一定通过哈夫曼算法得到。任何能压缩到最优长度的前缀编码都应被判为正确。

二、 解题思路

    考察哈夫曼编码性质，哈夫曼编码不唯一，但是长度肯定唯一，求出带权路径长度即可。

三、 程序设计

先将每个字符出现频率看作权值存进数组并进行升序排序
while(数组不为空)
    拿出数组最小的两个元素求和，并将结果插入数组
    数组按升序排序
最后一个在数组中的元素即为哈夫曼编码长度
if(截取字符串判断输入的编码为其他结点的前缀)
    返回NO
if(输入的编码长度 = 哈夫曼编码长度)
    返回NO
返回YES

四、 程序详解及运行结果

#include  
#include  
#include  
#include  
using namespace std;


int main() {
     
    int n, tem;
    char t;
    cin >> n;
    map<char, int>a;
    vector<int>b;
    for (int i = 0; i < n; ++i) {
     
        cin >> t >> tem;
        a[t] = tem;
        b.push_back(tem);
    }
    sort(b.begin(), b.end());
    int sum = 0;
    while (b.size() > 1) {
     
        int temp = b[0] + b[1];
        b.erase(b.begin() + 0);
        b.erase(b.begin() + 0);
        b.push_back(temp);
        sum += temp;
        sort(b.begin(), b.end());
    }
    int m;
    cin >> m;
    char s[1001];
    string ss[1001];
    for (int i = 0; i < m; ++i) {
     
        for (int j = 0; j < n; ++j) {
     
            cin >> s[j];
            cin >> ss[j];
        }
        int x = 0, flag = 0;
        for (int j = 0; j < n; ++j) {
     
            for (int k = j + 1; k < n; ++k) {
     
                int p = min(ss[j].length(), ss[k].length());
                if (ss[j].substr(0, p) == ss[k].substr(0, p)) {
     
                    flag = 1;
                    break;
                }
            }
            if (!flag) {
     
                auto it = a.find(s[j]);
                x += (ss[j].length() * it->second);
            }
            else
                break;
        }
        if (!flag && x == sum)
            cout << "Yes" << endl;
        else
            cout << "No" << endl;

    }
    return 0;
}

五、 问题及解决过程

    声明下标，利用线性表进行模拟实现优先级队列，要注意每次插入新的权时都要重新给数组排序。

实验六 图的存储 ：汉密尔顿回路

一、 题目

7-2 汉密尔顿回路

    著名的“汉密尔顿（Hamilton）回路问题”是要找一个能遍历图中所有顶点的简单回路（即每个顶点只访问 1 次）。本题就要求你判断任一给定的回路是否汉密尔顿回路。
输入格式:
    首先第一行给出两个正整数：无向图中顶点数 N（2
输出格式:
    对每条待检回路，如果是汉密尔顿回路，就在一行中输出"YES"，否则输出"NO"。

二、 解题思路

    考察图的遍历。遍历同一个点两次，两点间没有通路或者顶点没有全部遍历，便说明不是汉密尔顿回路。

三、 程序设计

读入邻接矩阵
if(回路顶点数!=d顶点总数)
    不是汉密尔顿回路
if(回路第一个点与最后一个点不一样)
    不是汉密尔顿回路
声明bool类型数组
for(顶点 in 回路)
    顶点为true
    if(当前顶点与上一个顶点不连通)
        不是汉密尔顿回路
if(bool数组全为true)
    是汉密尔顿回路
else
    不是汉密尔顿回路

四、 程序详解及运行结果

#include 
#include
using namespace std;
int main() {
     
    int k, n, m, x, y;
    cin >> n >> m;
    int N = 2 * n;
    vector<vector<int>>a(N, vector<int>(N, 0));
    for (int i = 0; i < m; ++i) {
     
        cin >> x >> y;
        a[x][y] = 1;
        a[y][x] = 1;
    }
    cin >> k;
    while (k--) {
     
        int h, t;
        cin >> h;
        if (h != n + 1) {
     
            cout << "NO" << endl;
            for (int i = 0; i < h; ++i) {
     
                cin >> t;
            }
            continue;
        }
        vector<int>c(N);
        vector<bool>b(N, false);
        int flag = 1;
        cin >> c[0];
        b[c[0]] = true;
        for (int j = 1; j < h; ++j) {
     
            cin >> c[j];
            if (!a[c[j]][c[j - 1]]) {
     
                flag = 0;
            }
            b[c[j]] = true;
        }
        if (c[h - 1] != c[0])
            flag = 0;
        for (int j = 1; j <= n; ++j) {
     
            if (!b[j]) {
     
                flag = 0;
                break;
            }
        }
        if (flag)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

五、 问题及解决过程

    如果经过的点数不为顶点数，或第一个点与最后一个点不同，便可以直接返回不是汉密尔顿回路。要注意判断经过一个点两次的情况。

实验七 贪心算法 ：月饼

一、 题目

7-1 月饼

    月饼是中国人在中秋佳节时吃的一种传统食品，不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量，请你计算可以获得的最大收益是多少。
    注意：销售时允许取出一部分库存。样例给出的情形是这样的：假如我们有 3 种月饼，其库存量分别为 18、15、10 万吨，总售价分别为 75、72、45 亿元。如果市场的最大需求量只有 20 万吨，那么我们最大收益策略应该是卖出全部 15 万吨第 2 种月饼、以及 5 万吨第 3 种月饼，获得 72 + 45/2 = 94.5（亿元）。
输入格式:
    每个输入包含一个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N 表示月饼的种类数、以及不超过 500（以万吨为单位）的正整数 D 表示市场最大需求量。随后一行给出 N 个正数表示每种月饼的库存量（以万吨为单位）；最后一行给出 N 个正数表示每种月饼的总售价（以亿元为单位）。数字间以空格分隔。
输出格式:
    对每组测试用例，在一行中输出最大收益，以亿元为单位并精确到小数点后 2 位。

二、 解题思路

    要想获取最大收益，通过售价与库存的比值降序排序，并按需求量输出即可。

三、 程序设计

声明一个含有库存量和售价的结构体
编写用于排序比较售价与库存比值的函数
然后读入数据并进行排序即可

四、 程序详解及运行结果

#include 
#include
#include
using namespace std;
struct yb{
     
    double kucun;
    double shoujia;
};
bool cmp(yb a, yb b){
     
    return (a.shoujia / a.kucun) > (b.shoujia / b.kucun);
}
int main(){
     
    double n, m, ans = 0;
    cin >> n >> m;
    vector<yb> a(n);
    for (int i = 0; i < n; i++)
        cin >> a[i].kucun;
    for (int i = 0; i < n; i++)
        cin >> a[i].shoujia;
    sort(a.begin(), a.end(), cmp);
    for (int i = 0; i < n; i++){
     
        if (m > a[i].kucun){
     
            m -= a[i].kucun;
            ans += a[i].shoujia;
        }
        else{
     
            ans += (a[i].shoujia / a[i].kucun * m);
            break;
        }
    }
    printf("%.2f", ans);
    return 0;
}

五、 问题及解决过程

    为避免声明多个数组来存储数据，下标因排序变得混乱，定义结构体来更高效的存储，排序，处理数据。

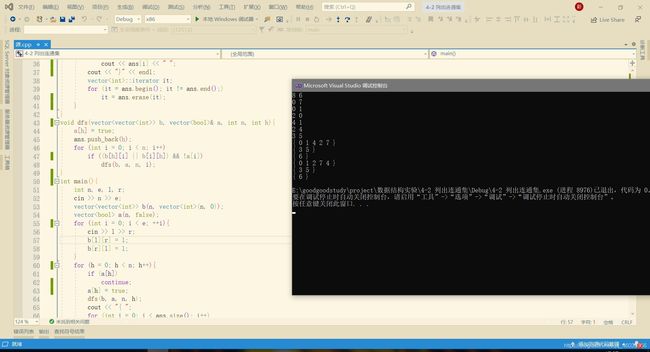
实验八 图的应用 ：列出连通集

一、 题目

7-2 列出连通集

    给定一个有N个顶点和E条边的无向图，请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时，假设我们总是从编号最小的顶点出发，按编号递增的顺序访问邻接点。
输入格式:
    输入第1行给出2个整数N(0
输出格式:
    按照"{ v1 v2 … vk }"的格式，每行输出一个连通集。先输出DFS的结果，再输出BFS的结果。

二、 解题思路

    考察利用图的遍历，对图的连通性进行判断，并列出深搜与广搜的连通集。

三、 程序设计

提前声明一个数组存储要输出的连通集
声明一个用于深搜的栈和一个用于广搜的队列
读入图
对图进行深度优先搜索与广度优先搜索
每找到一个连通集便输出
输出后清空数组

四、 程序详解及运行结果

#include 
#include 
#include 
#include 
using namespace std;
queue<int> bfss;
stack<int> dfss;
int h;
vector<int> ans;
void bfs(vector<vector<int>> b, vector<bool>& a, int n){
     
    for (h = 0; h < n; h++){
     
        if (a[h])
            continue;
        bfss.push(h);
        ans.push_back(h);
        a[h] = true;
        while (!bfss.empty()){
     
            int temp = bfss.front();
            bfss.pop();
            for (int k = 0; k < n; k++){
     
                if ((b[temp][k] || b[k][temp]) && !a[k]){
     
                    a[k] = true;
                    ans.push_back(k);
                    bfss.push(k);
                }
            }
        }
        cout << "{ ";
        for (int i = 0; i < ans.size(); i++)
            cout << ans[i] << " ";
        cout << "}" << endl;
        vector<int>::iterator it;
        for (it = ans.begin(); it != ans.end();)
            it = ans.erase(it);
    }
}
void dfs(vector<vector<int>> b, vector<bool>& a, int n, int h){
     
    a[h] = true;
    ans.push_back(h);
    for (int i = 0; i < n; i++)
        if ((b[h][i] || b[i][h]) && !a[i])
            dfs(b, a, n, i);
}
int main(){
     
    int n, e, l, r;
    cin >> n >> e;
    vector<vector<int>> b(n, vector<int>(n, 0));
    vector<bool> a(n, false);
    for (int i = 0; i < e; ++i){
     
        cin >> l >> r;
        b[l][r] = 1;
        b[r][l] = 1;
    }
    for (h = 0; h < n; h++){
     
        if (a[h])
            continue;
        a[h] = true;
        dfs(b, a, n, h);
        cout << "{ ";
        for (int i = 0; i < ans.size(); i++)
            cout << ans[i] << " ";
        cout << "}" << endl;
        vector<int>::iterator it;
        for (it = ans.begin(); it != ans.end();)
            it = ans.erase(it);
    }
    for (int i = 0; i < n; i++)
        a[i] = false;
    bfs(b, a, n);
    return 0;
}

五、 问题及解决过程

    判断连通性即可，要注意及时清空数组，避免输出时出现错误。

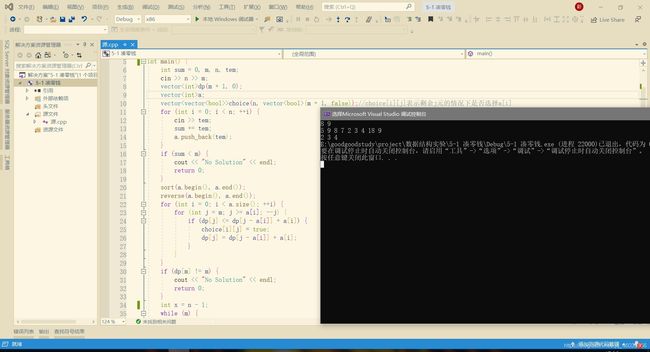
实验九 动态规划 ：凑零钱

一、 题目

7-1 凑零钱

    韩梅梅喜欢满宇宙到处逛街。现在她逛到了一家火星店里，发现这家店有个特别的规矩：你可以用任何星球的硬币付钱，但是绝不找零，当然也不能欠债。韩梅梅手边有 104 枚来自各个星球的硬币，需要请你帮她盘算一下，是否可能精确凑出要付的款额。
输入格式:
    输入第一行给出两个正整数：N（≤104）是硬币的总个数，M（≤102）是韩梅梅要付的款额。第二行给出 N 枚硬币的正整数面值。数字间以空格分隔。
输出格式:
    在一行中输出硬币的面值 V1≤V2≤⋯≤Vk，满足条件 V1 +V2 +…+Vk=M。数字间以 1 个空格分隔，行首尾不得有多余空格。若解不唯一，则输出最小序列。若无解，则输出 No Solution。
    注：我们说序列{ A[1],A[2],⋯ }比{ B[1],B[2],⋯ }“小”，是指存在 k≥1 使得 A[i]=B[i] 对所有 i

二、 解题思路

    考察动态规划，求每种面值硬币只有一个的情况下取最多硬币凑出目标的情况。可以先利用深搜得到答案后，再用剪枝的方法简化程序，列出所有情况及选择到数组中，就成了动态规划。

三、 程序设计

定义bool类型二维数组choice
和一维数组a来存储所有零钱面额
声明一维数组来储存当前最小序列凑出的金额
choice[i][j]表示剩余j元的情况下是否选择a[i]
因为要求最小序列，故将a数组从大到小排序
for(面值 in a)
    for(金额 in 目标金额 - 面值)  从大到小遍历
        if(当前金额 <= 更小序列凑出的金额)
            当前金额 = 更小序列凑出的金额
            choice该位置赋值为true
若目标金额 != 数组对应位置最小序列凑出的金额
    返回无解
通过choice数组标记输出答案

四、 程序详解及运行结果

#include
#include
#include
using namespace std;
int main() {
     
    int sum = 0, m, n, tem;
    cin >> n >> m;
    vector<int>dp(m + 1, 0);
    vector<int>a;
    vector<vector<bool>>choice(n, vector<bool>(m + 1, false));
    //choice[i][j]表示剩余j元的情况下是否选择a[i]
    for (int i = 0; i < n; ++i) {
     
        cin >> tem;
        sum += tem;
        a.push_back(tem);
    }
    if (sum < m) {
     
        cout << "No Solution" << endl;
        return 0;
    }
    sort(a.begin(), a.end());
    reverse(a.begin(), a.end());
    for (int i = 0; i < a.size(); ++i) {
     
        for (int j = m; j >= a[i]; --j) {
     
            if (dp[j] <= dp[j - a[i]] + a[i]) {
     
                choice[i][j] = true;
                dp[j] = dp[j - a[i]] + a[i];
            }
        }
    }
    while (m != 0) {
     
        int h = m;
        cout <<"M 为"<< h << "时，对应解为 ：";
        if (dp[h] != h) {
     
            cout << "No Solution" << endl;
            return 0;
        }
        int x = n - 1;
        while (h) {
     
            while (!choice[x][h]) --x;
            cout << a[x];
            h -= a[x];
            x--;
            if (h)
                cout << ' ';
        }
        cout << endl;
        m--;
    }
    return 0;
}

M从1~9对应样例一的所有解为

五、 问题及解决过程

    先在草稿纸上演算，找到方法后再进行构思操作，应注意从大到小遍历零钱面值，if中条件应为 <= ，这样每一个符合要求的值都是一个更小的序列。

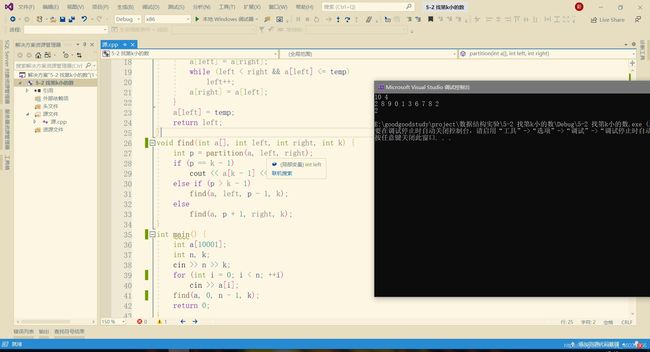
实验十 分治算法 ：找第k小的数## 一、 题目

一、 题目

7-2 找第k小的数

    *设计一个平均时间为O(n)的算法，在n(1<=n<=1000)个无序的整数中找出第k小的数。
    提示：函数int partition(int a[],int left,int right)的功能是根据a[left]a[right]中的某个元素x（如a[left])对a[left]a[right]进行划分，划分后的x所在位置的左段全小于等于x,右段全大于等于x,同时利用x所在的位置还可以计算出x是这批数据按升非降序排列的第几个数。因此可以编制int find(int a[],int left,int right,int k)函数，通过调用partition函数获得划分点，判断划分点是否第k小，若不是，递归调用find函数继续在左段或右段查找。
*
输入格式:
    输入有两行：第一行是n和k，0
输出格式:
    输出第k小的数

二、 解题思路

    考察分治算法，找第k小的数的过程类似快速排序，通过改写快速排序函数得出结果。

三、 程序设计

int partition(int a[],int left,int right)函数，其功能是根据a[left]a[right]进行划分，
划分后的x所在位置的左段全小于等于x,右段全大于等于x,
同时利用x所在的位置还可以计算出x是这批数据按升非降序排列的第几个数
int find(int a[],int left,int right,int k)函数，通过调用partition函数获得划分点，
判断划分点是否第k小，若不是，递归调用find函数继续在左段或右段查找。

四、 程序详解及运行结果

#include 
#include
using namespace std;
int partition(vector<int>&a, int left, int right) {
     
    int temp = a[left];
    int l = left, r = right;
    left++;
    while (left != right) {
     
        while (left < right && a[right] > temp)
            right--;
        while (left < right && a[left] < temp)
            left++;
        if(left < right)
            swap(a[left], a[right]);
    }
    a[l] = a[left];
    a[left] = temp;
    return left;
}
void find(vector<int>&a , int left, int right, int k) {
     
    int p = partition(a, left, right);
    if (p == k - 1)
        cout << a[k - 1] << endl;
    else if (p > k - 1)
        find(a, left, p - 1, k);
    else
        find(a, p + 1, right, k);
}
int main() {
     
    
    int n, k;
    cin >> n >> k;
    vector<int>a(n);
    for (int i = 0; i < n; ++i) 
        cin >> a[i];
    find(a, 0, n - 1, k);
    return 0;
}

五、 问题及解决过程

    注意传参时要加&符号，否则无法对数组中元素顺序进行修改。