DolphinDB Database 丨量化交易回测系列二：多因子Alpha策略回测

本系列文章将会介绍如何使用DolphinDB优雅而高效的实现量化交易策略回测。本文将介绍在华尔街广泛应用的多因子Alpha策略的回测。多因子模型是量化交易选股中最重要的一类模型，基本思路是找到某些和回报率最相关的指标，并根据这些指标，构建股票投资组合（做多正相关的股票，做空负相关的股票）。多因子模型中，单独一个因子的个股权重一般实现多空均衡（市场中性），没有暴露市场风险的头寸（beta为0，所以称之为alpha策略），能实现绝对收益。多个因子之间相互正交，方便策略配置，实现回报和风险的最优控制。另外，相比于套利策略（通常可以实现更高的sharpe ratio，但是scale不好），多因子alpha策略有很好的scale，可以配置大量的资金。多因子Alpha策略在对冲基金中的使用非常普遍。

1. 生成因子

本文的重点是实现多因子Alpha策略的回测框架。因子不是重点，这部分通常由金融工程师或策略分析师来完成。为了方便大家理解，文章以动量因子、beta因子、规模因子和波动率因子4个常用的风险因子为例，介绍如何在 DolphinDB database 中实现多因子回测。

输入数据表inData包含6个字段：sym （股票代码）, date（日期）, close （收盘价）, RET（日回报）, MV（市值）, VOL（交易量）

def genSignals(inData){
	USstocks = select sym, date, close, RET, MV from inData where weekday(date) between 1:5, close>5, VOL>0, MV>100000 order by sym, date
	update USstocks set prevMV=prev(MV), cumretIndex=cumprod(1+RET), signal_size=-sqrt(MV), signal_vol=-mstd(RET, 21)*sqrt(252) context by sym
	update USstocks set mRet = wavg(RET, prevMV) context by date
	update USstocks set signal_mom = move(cumretIndex,21)/move(cumretIndex,252)-1, signal_beta=mbeta(RET, mRet, 63) from USstocks context by sym
	return select sym, date, close, RET as ret, signal_size, signal_beta, signal_vol, signal_mom from USstocks where date>=1991.01.01
}

DolphinDB函数说明：

abs：取绝对值。

prev：把向量中的所有元素向右移动一个位置。

cumprod：计算累计乘积。

sqrt：计算平方根。

mstd(X, k)：计算移动标准差。

wavg(X, k)：计算加权平均数。

move(X, k)：如果k为正数，则把向量的所有元素向右移动k个位置，如果k为负数，则把向量的所有元素向左移动k个位置。

mbeta(X, Y, k)：计算普通最小二乘回归的系数估计。

genSignals 函数说明：

首先数据过滤，选择市值较高的股票在交易日中的数据。接着使用过滤后的数据计算4个风险因子：

• 规模因子（signal_size）：MV的平方根的相反数
• 波动率因子（signal_vol）：过去一个月的股价波动率的相反数
• 动量因子（signal_mom）：过去12个月（去除最近一个月）的动量因子
• beta因子（signal_beta）：利用过去三个月的数据计算个股跟市场的beta

2. 回测框架

多因子Alpha策略的回测框架包含3个部分。首先是在每个历史周期上，生成每个股票在每个策略上的权重。一个历史周期上的所有仓位可以成为一个tranche。然后根据tranche的持有时间，生成每一个股票在每一个tranche的每一个策略上每一天的仓位和盈亏。最后统计分析每个策略和所有策略的业绩。

2.1 计算历史周期的投资仓位

首先定义一个函数formPeriodPort计算一个周期（一天）的股票仓位。然后使用并行计算获得历史上每一个周期的投资仓位。

2.1.1 计算一天的股票投资组合

这一步的输入是每一个股票在不同因子上的值，输出是每一个股票在每一个因子上的投资权重。股票权重要满足两个条件：（1）一个因子中所有股票的权重和为零，也就是说多空均衡。（2）不同因子之间相互正交，也就是说第i个因子的权重wi和第j个因子的值sj的内积为0（i<>j)。为了实现上述目标，我们引入了因子矩阵（矩阵的每一列表示一个因子，每一行表示一个股票），并且将单位因子（所有元素均为1）添加到因子矩阵中。

实践中，还需要考虑的一个问题是，去除权重较小的股票。一个股票池有几千个股票，大部分的股票获得的权重很小，几乎可以忽略。我们定义了一个嵌套函数f来调整单个因子中股票的权重。

函数formPeriodPort的输入参数有3个：

• signals 是由genSignals函数生成的数据表，包含8个字段：股票代码、日期、收盘价格、回报率和4个因子。
• signalNames 是所有因子的名称，用向量表示。
• stockPercentile 用于控制股票的数量。

函数的输出是一个数据表，存储一天的股票投资组合，包括4个字段：tranche, sym, signalIdx, exposure。

def formPeriodPort(signals, signalNames, stockPercentile){
	stockCount = signals.size()
	signalCount = signalNames.size()
	tranche = signals.date.first()
	
        //demean all signals and add a unit column to the signal matrix
	sigMat = matrix(take(1, stockCount), each(x->x - avg(x), signals[signalNames]))

	//form weight matrix. 
	transSigMat = sigMat.transpose()
	weightMat = transSigMat.dot(sigMat).inv().dot(transSigMat).transpose()[1:]

	/* form exposures. allocate two dollars on each signal, one for long and one for short
	   trim small weights. In practice, we don't want to trade too many stocks */
	f = def(sym, tranche, stockPercentile, signalVec, signalIdx){
		t = table(sym, signalVec as exposure, iif(signalVec > 0, 1, -1) as sign)
		update t set exposure = exposure * (abs(exposure) < percentile(abs(exposure), stockPercentile)) context by sign
		update t set exposure = exposure / sum(exposure).abs() context by sign
		return select tranche as tranche, sym, signalIdx as signalIdx, exposure from t where exposure != 0
	}
	return loop(f{signals.sym, tranche, stockPercentile}, weightMat, 1..signalCount - 1).unionAll(false)
}

DolphinDB函数说明：

size：返回向量中元素的个数

first：返回第一个元素

matrix：构建矩阵

transpose：矩阵转置

dot：矩阵或向量内积

inv：矩阵求逆

iif(condition, trueResult, falseResult)：如果满足条件condition，则返回trueResult，否则返回falseResult。它相当于对每个元素分别运行if...else语句。

loop(func,args)：高价模板函数，把函数func应用到参数args的每一个元素上，并将结果汇总到一个元组中。如果args包含三个k个参数，每个参数的长度是n，那么loop将运行n次。

unionAll：合并多个表

 

2.1.2 计算过去每天的股票投资组合

回测时使用 的数据量非常庞大，因此我们把数据放到内存的分区数据库中，然后使用并行计算。如果想要了解更多关于分区数据库的内容，可以参考DolphinDB分区数据库教程。我们把genSignals函数生成的数据保存到分区表partSignals中，一个分区表示一天。接着，创建一个分区表ports，用于保存计算出来的股票投资组合，一个分区表示一年。然后，使用 map-reduce函数，把formPeriodPort函数应用到每一天，把每个结果合并到分区表ports中。

def formPortfolio(signals, signalNames, stockPercentile){
	dates = (select count(*) from signals group by date having count(*)>1000).date.sort()
	db = database("", VALUE, dates)
	partSignals = db.createPartitionedTable(signals, "signals", `date).append!(signals)
	db = database("", RANGE, datetimeParse(string(year(dates.first()) .. (year(dates.last()) + 1)) + ".01.01", "yyyy.MM.dd"))
	symType = (select top 10 sym from signals).sym.type()
	ports = db.createPartitionedTable(table(1:0, `tranche`sym`signalIdx`exposure, [DATE,symType,INT,DOUBLE]), "", `tranche)
 	return mr(sqlDS(), formPeriodPort{,signalNames,stockPercentile},,unionAll{,ports})
} 
  
DolphinDB函数说明：
 
  
sort：把向量中的元素排序
 
  
database(directory, [partitionType], [partitionScheme], [locations])：创建数据库。如果directory为空，则创建内存数据库。
 
  
createPartitionedTable(dbHandle, table, [tableName], partitionColumns)：在数据库中创建分区表。
 
  
datatimeParse(X, format)：把字符串转换成DolphinDB中时间类型数据。
 
  
unionAll：合并表
 
  
type：返回数据类型的ID。
 
  
mr(ds, mapFunc, [reduceFunc], [finalFunc], [parallel=true])：map-reduce函数。
 
  
 
 
  
2.2 计算仓位和盈亏
 
  
这一步的任务是根据持有的仓位以及持有时间，生成每一个股票在每一个tranche的每一个因子上每一天的仓位和盈亏。首先定义一个嵌套函数来f来计算部分股票投资仓位的盈亏，接着把嵌套函数应用到所有股票投资组合（使用mr函数），计算所有股票投资组合的盈亏，并把结果保存到分区表pnls中。
 
  
函数caclStockPnL的输入参数包括：
 
  
 
   
ports: 每一天的投资组合表，包括4个字段 tranche, sym, signalIdx, exposure
 
   
dailyRtn：股票每天的回报表，包括3个字段 date, sym, ret
 
   
holdingDays: 股票持有的天数
 
  
 
  
函数的输出是股票的盈亏明细表，包括字段8个字段 date, sym, signalIdx, tranche, age, ret, exposure, pnl
 
  
def calcStockPnL(ports, dailyRtn, holdingDays){
	ages = table(1..holdingDays as age)
	dates = sort exec distinct(tranche) from ports
	dictDateIndex = dict(dates, 1..dates.size())
        dictIndexDate = dict(1..dates.size(), dates)
        lastDaysTable = select max(date) as date from dailyRtn group by sym
	lastDays = dict(lastDaysTable.sym, lastDaysTable.date)

        // define a anonymous function to calculate the pnl for a part of the porfolios.
	f = def(ports, dailyRtn, holdingDays, ages, dictDateIndex, dictIndexDate,lastDays){
		pos = select dictIndexDate[dictDateIndex[tranche]+age] as date, sym, signalIdx, tranche, age, take(0.0,size age) as ret, exposure, take(0.0,size age) as pnl from cj(ports,ages) where isValid(dictIndexDate[dictDateIndex[tranche]+age]), dictIndexDate[dictDateIndex[tranche]+age]<=lastDays[sym]
		update pos set ret = dailyRtn.ret from ej(pos, dailyRtn,`date`sym)
		update pos set exposure = exposure*cumprod(1+ret) from pos context by tranche, signalIdx, sym
		update pos set pnl = exposure*ret/(1+ret)
		return pos
	}

        // calculate pnls for all portfolios and save the result to a partitioned in-memory table pnls
	db = database("", RANGE, datetimeParse(string(year(dates.first()) .. (year(dates.last()) + 1)) + ".01.01", "yyyy.MM.dd"))
	symType = (select top 10 sym from ports).sym.type()
	modelPnls = table(1:0, `date`sym`signalIdx`tranche`age`ret`exposure`pnl, [DATE,symType,INT,DATE,INT,DOUBLE,DOUBLE,DOUBLE])
	pnls = db.createPartitionedTable(modelPnls, "", `tranche)
 	return mr(sqlDS(), f{,dailyRtn,holdingDays,ages,dictDateIndex, dictIndexDate,lastDays},,unionAll{,pnls})
}     

DolphinDB函数说明：

dict(key, value)：创建字典。

cj(leftTable, rightTable) ：交叉连接两个表。

isValid：检查元素是否为NULL。如果不是NULL，则返回1，如果是NULL，则返回0。

ej(leftTable, rightTable, matchingCols, [rightMatchingCols]) ：等值连接两个表。

 

3. 运行实例

我们以美国股市为例，运行多因子Alpha策略回测。输入的股票日数据表USPrices包含6个字段：sym （股票代码）, date（日期）, close （收盘价）, RET（日回报）, MV（市值）和VOL（交易量）。

//加载数据
USPrices = ...

holdingDays = 5
stockPercentile = 20
signalNames = `signal_mom`signal_vol`signal_beta`signal_size

//生成因子
signals=genSignals(USPrices)

//计算每天的股票投资组合
ports = formPortfolio(signals, signalNames, stockPercentile)

//计算盈亏
dailyRtn = select sym,date,ret from signals
pos = calcStockPnL(ports, dailyRtn, holdingDays)

//绘制四个因子的累计盈亏走势图
pnls = select sum(pnl) as pnl from pos group by date, signalIdx
factorPnl = select pnl from pnls pivot by date, signalIdx
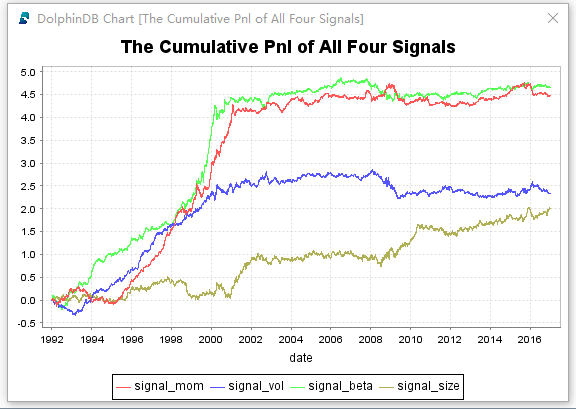
plot(each(cumsum,factorPnl[`C0`C1`C2`C3]).rename!(signalNames), factorPnl.date, "The Cumulative Pnl of All Four Signals")

//绘制动量因子不同持仓日的累计盈亏走势图
pnls = select sum(pnl) as pnl from pos where signalIdx=0 group by date, age
momAgePnl = select pnl from pnls pivot by date, age
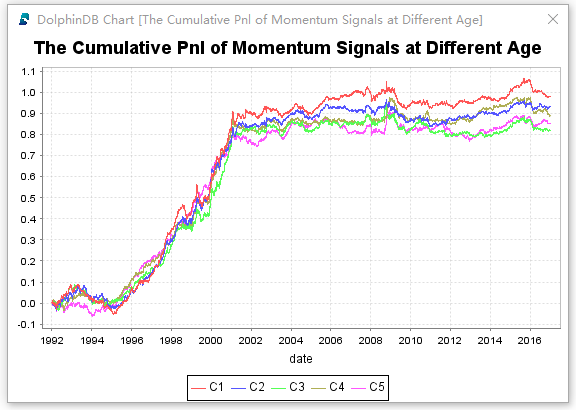
plot(each(cumsum,momAgePnl[`C1`C2`C3`C4`C5]).rename!(`C1`C2`C3`C4`C5), momAgePnl.date)

4个因子的累计盈亏走势图

动量因子的累计盈亏走势图

DolphinDB虽然是一个通用的分布式时序数据库，但因为内置极其高效的多范式编程语言，用于量化交易，开发效率非常高。上面的多因子回测框架，仅用了3个自定义函数，50余行代码。DolphinDB的运行效率更是惊人，对美国股市25年中市值较高的股票按日进行回测，最后产生的盈亏明细表包含1亿余条记录。如此复杂的计算量，在单机（4核）上执行耗时仅50秒。

 

4. 讨论

前面的回测框架，仅仅解决了多因子策略的一部分问题，也就是说单个因子中股票的配置。我们还有两个重要的问题需要解决：（1）多个因子之间，如何配置权重，平衡投资的回报和风险。（2）一个新的因子有没有带来额外的Alpha，换句话说，一个新的因子是不是可以有已经存在的多个因子来表示，如果可以，那么这个新因子可能没有存在的必要。下一篇文章，我们会介绍如何使用DolphinDB来回答上面两个问题。