cs224w 图神经网络 学习笔记（十）Deep Generative Models for Graphs
课程链接：CS224W: Machine Learning with Graphs
课程视频：【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
目录
-
- 1. 前言
- 2. Problem of Graph Generation 问题的引出以及难点
- 3. ML Basics for Graph Generation
- 4. GraphRNN——生成真实的网络
-
- 4.1 Model Graph as Sequences 将图的生成问题转换成序列生成问题
- 4.2 GraphRNN
- 4.3 模型优化——图节点的编号策略
1. 前言
我们上节课讨论了对网络进行编码的架构。同时，我们也介绍了GCN的核心思想——Aggregate neighbours，并讨论了如何使用神经网络去实现。也就说，我们之前讨论的，是如何对网络进行embedding；我们今天要讲的是，如何从embedding生成网络。
2. Problem of Graph Generation 问题的引出以及难点
网络的生成有很多实际的应用：
- Generation – Gives insight into the graph formation process 可以了解网络的形成过程（例如人际网的发展、交通网的扩张等）
- Anomaly detection – abnormal behavior, evolution 异常检测
- Predictions – predicting future from the past 预测（例如网络发展的演化等）
- Simulations of novel graph structures 对全新的网络结构进行仿真
- Graph completion – many graphs are partially observed 网络的补全（例如知识图谱补全等）
- "What if” scenarios
问题的引入——有真实的网络 G G G，和人造的网络 G ′ G' G′，那么：
- 怎样的生成模型是好的？
- 我们如何拟合模型并使用它生成网络?
网络的生成主要涉及两个任务：
- Generate graphs that are similar to a given set of graphs 生成与给定图集相似的图——这个是我们今天的主要内容
- Goal-directed graph generation 目标导向的网络生成 ，即生成优化给定目标/约束的网络（例如药物分子生成/优化）
可以说，网络生成是有趣的，也是很难的任务，它的难主要体现在以下几个方面：
- 第一，输出空间很大且是可变的。网络一般会采用邻接矩阵表示节点和边，对于 n n n个节点的网络来说，它的输出空间就是 n 2 n^2 n2的矩阵；另外，和一般的机器学习不同，其输出空间是不确定的，会随着不同的网络变化。
- 第二对于同一个网络，其邻接矩阵并不是唯一确定的，和节点编号的顺序有关。
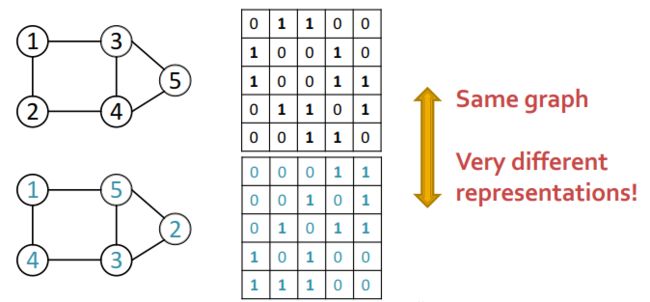
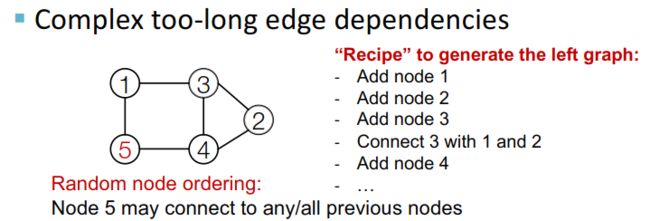
- 第三，网络的生成过程中，点和边有复杂的依赖关系。比如我们要生成一个六个节点的环，我们需要记住所有的历史步骤，对于一些复杂的图来说，内存和效率极有挑战。
3. ML Basics for Graph Generation
假设我们要通过一组节点数据 { x i } \{x_i\} { xi}来学习网络的生成模型。
p d a t a ( x ) p_{data}(x) pdata(x)是数据的分布（data distribution），实际上我们并不可能知道这个分布，但是我们可以通过对 x i x_i xi的采样（sampling）来得到这个分布，即 x i ∽ p d a t a ( x ) x_i \backsim p_{data}(x) xi∽pdata(x)。
p m o d e l ( x ; θ ) p_{model}(x;\theta) pmodel(x;θ)是模型（model），参数 θ \theta θ用来估计 p d a t a ( x ) p_{data}(x) pdata(x)。
那么，我们的目标就是：
（1）让 p m o d e l ( x ; θ ) p_{model}(x;\theta) pmodel(x;θ)接近于 p d a t a ( x ) p_{data}(x) pdata(x)；
核心理论——极大似然估计
（2）确保我们可以从 p m o d e l ( x ; θ ) p_{model}(x;\theta) pmodel(x;θ)采样，并生成网络。
这里的函数 f ( ⋅ ) f(·) f(⋅)采用深度神经网络实现。
4. GraphRNN——生成真实的网络
4.1 Model Graph as Sequences 将图的生成问题转换成序列生成问题
网络的生成是通过不断地增加节点和边来实现的。
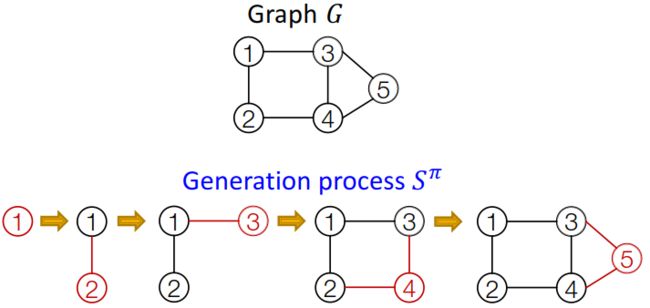
对应一个确定的节点顺序 π \pi π，图 G G G可以表示为节点和边的序列 S π S^{\pi} Sπ：
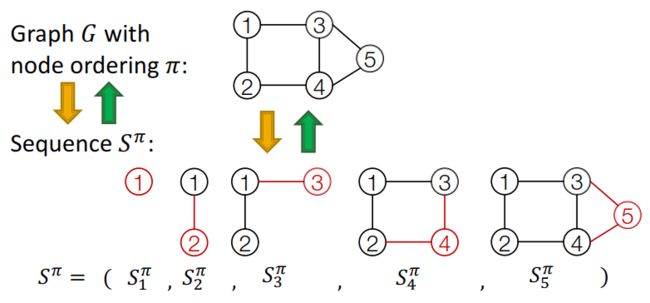
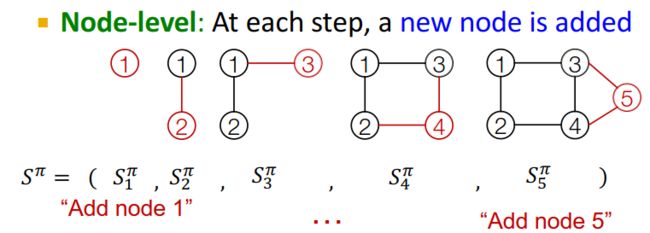
S π S^{\pi} Sπ实际上是序列的序列。对应的每一个序列 S i π S_i^{\pi} Siπ，都有两个层次的操作：
- 节点操作——增加节点，序列 S i π S_i^{\pi} Siπ只有一步操作
- 边的操作——序列 S i π S_i^{\pi} Siπ中的每一步表示增加一条边
那么，我们就可以将图的生成问题转换成一个序列的生成问题。这样一来，（对于无向图来说），我们只需要保存邻接矩阵的一半就行了。
A graph + a node ordering = A sequence of sequences!
那么接下来，我们需要解决的就是两个过程：
- 新的节点的生成——节点序列的生成
- 对于新生成的节点，生成其相关联的边——边序列的生成
而解决序列问题，我们自然而然地就能想到利用RNN来实现。
4.2 GraphRNN
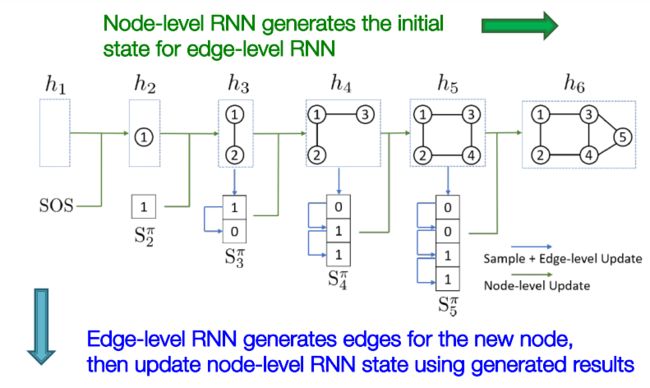
GraphRNN包括两个部分：
- node-level RNN——生成edge-level RNN的初始状态
- edge-level RNN——为新节点创建相关的边，并将结果更新到node-level RNN的状态中。
那么，我们怎样利用RNN来生成序列呢？
对于一个RNN单元来说，有状态 s t s_t st，输入 x t x_t xt，输出 y t y_t yt。
对于序列的表示，可以将RNN单元重复连接。开始和结束都定义一个标识符，开始的标识符 s 0 = S O S s_0=SOS s0=SOS，结束的标识符 y T = E O S y_T=EOS yT=EOS；上一个状态的输出是下一个状态的输入，即 x t + 1 = y t x_{t+1}=y_t xt+1=yt。
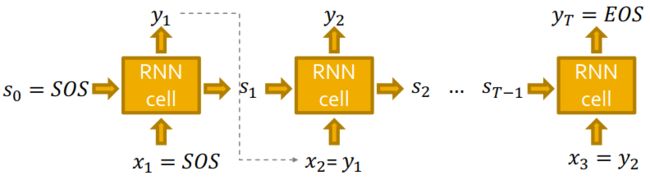
在上述模型的基础上，我们需要给RNN模型增加随机性。首先，我们要明确的是，我们的目标是使用RNN来估计 ∏ k = 1 n p m o d e l ( x t ∣ x 1 , ⋯ , x t − 1 ; θ ) \prod_{k=1}^n p_{model}(x_t|x_1, \cdots, x_{t-1}; \theta) ∏k=1npmodel(xt∣x1,⋯,xt−1;θ)。那么， x t + 1 x_{t+1} xt+1是 y t : x t + 1 ∽ y t y_t:x_{t+1} \backsim y_t yt:xt+1∽yt的取样。
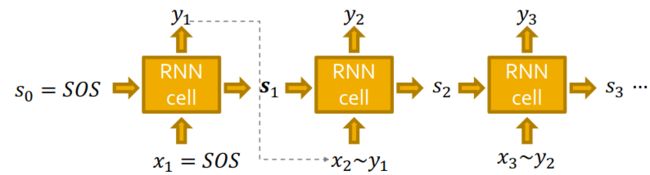
RNN每一步的输出是一个概率向量，下一个状态的输入时基于该概率向量的一个取样。
模型的测试
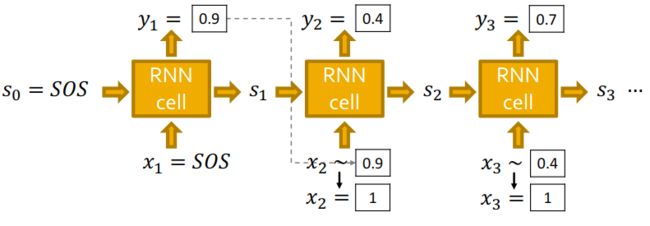
假设我们有一个已经训练好的模型， y y y服从伯努利分布， y 1 = 0.9 y_1=0.9 y1=0.9表示有0.9的概率生成1，即有边连接；有 1 − 0.9 = 0.1 1-0.9=0.1 1−0.9=0.1的概率生成0，即没有边连接。
模型训练
在进行模型训练的时候，有一个原则——Teacher Forcing，也就是加入我们检测到真实的边的序列为 [1,0,…]，在训练时我们用真实的这个序列作为输出。
损失函数定义为Binary cross entropy，训练目标是使损失函数最小化：
L = − [ y 1 ∗ log ( y 1 ) + ( 1 − y 1 ∗ ) log ( 1 − y 1 ) ] L=-[y_1^* \log(y_1)+(1-y_1^*)\log (1-y_1)] L=−[y1∗log(y1)+(1−y1∗)log(1−y1)]
y 1 ∗ y_1^* y1∗是真实结果。如果 y 1 ∗ = 1 y_1^*=1 y1∗=1，则 L = − log ( y 1 ) L=-\log(y_1) L=−log(y1)， y 1 y_1 y1越大（越接近 y 1 ∗ y_1^* y1∗）， L L L越小；如果 y 1 ∗ = 0 y_1^*=0 y1∗=0，则 L = − log ( 1 − y 1 ) L=-\log (1-y_1) L=−log(1−y1)， y 1 y_1 y1越小（越接近 y 1 ∗ y_1^* y1∗）， L L L越小。这样，就可以使预测值 y 1 y_1 y1越来越接近实际值 y 1 ∗ y_1^* y1∗。预测值 y 1 y_1 y1通过RNN计算得到，可以通过反向传播不断优化RNN的参数。
4.3 模型优化——图节点的编号策略
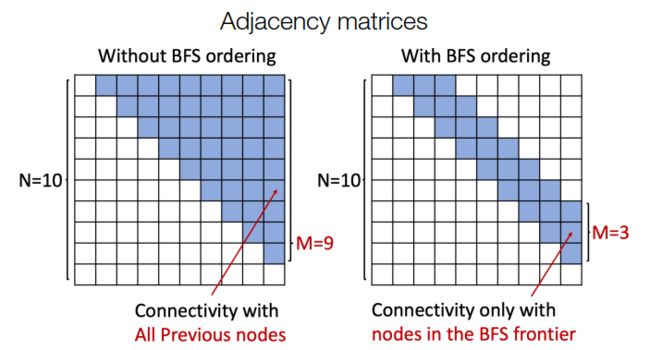
然而，我们还是面临一个问题，因为每一个新生成的点都有可能和之前的点进行关联，也就是说，当图的节点数量很大时，我需要记住很长的依赖关系来实现边的生成。
我们的解决方案，就是利用BFS（广度优先搜索）来给图的节点编号。
使用广度优先搜索进行编号，有两个优点：
- Reduce possible node orderings
- Reduce steps for edge generation
