CS224W笔记-第七课
CS224W笔记-第七课：图表征学习
前面几次课在不同程度上介绍了在图结构数据上的机器学习任务。总体而言，图上的机器学习包括（但不限于）下面3大任务：
- 点分类/回归
- 边预测/分类/回归
- 整图分类/回归
总传统的机器学习管道而言，一般都会有从原始数据到模型输入数据的特征工程的步骤，而这一步骤对于机器学习的性能影响巨大。因此，在现在的深度学习所擅长的一个点就是自动学习和获取这些特征。在图里，这就是图表征的学习。
图表征的目的：
高效地对图学习到不依赖于下游任务的特征。
图向量基本思想：
对于图，把基于邻接矩阵的节点的分布式表征(类似于one-hot编码)，学习到隐性的低维度的稠密的表征(向量/嵌入)，并用于下游的任务。
点表征学习
点表征学习(点向量)的目的：
学习到点的低维度向量，且若点-点它们在原始图中相似，则在向量空间里的点和点的向量也相似，即向量点积高。
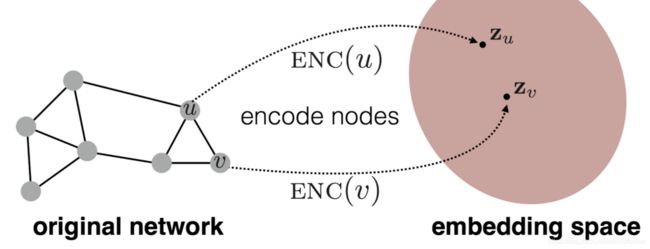
数学表示： s i m i l a r i t y ( u , v ) ≈ z v ⊤ z u \mathrm{similarity}(u, v) \approx {\mathrm{z}_v}^{\top}\mathrm{z}_u similarity(u,v)≈zv⊤zu
在这里，产生点向量的步骤就变成了3步：
- 定义一个编码器，由它完成点向量的生成；
- 定义相似度函数 s i m i l a r i t y \mathrm{similarity} similarity，计算原始图中的点的相似度；
- 通过损失函数，优化编码器的参数，完成最终的学习。
通过这个方式，可以看到，最重要的组件就是编码器和相似度函数。
其中，编码器的表示就是： E N C ( v ) = Z v \mathrm{ENC}(v)=\mathrm{Z}_v ENC(v)=Zv。
这个编码器可以像word2vec那样的仅仅是一个浅层的查找矩阵。但是对于图结构数据，还有其他的最新的方法，比如deepwalk，node2vec，TransE等。
同时，对于如何定义图中两个点的相似度也是一个充满创意的研究热点，不同的方法给出了不同的计算。
随机游走(Random Walk)构建点向量算法
随机游走的定义：
给定一个图和一个起始点，随机选择它的一个邻居节点，移动到这个邻居，然后再随机选择一个邻居。这个过程被称为图中的随机游走。
根据随机游走的定义，可以认为：如果两个点 u u u和 v v v出现在一次随机游走中，则它们是相似的。这就是随机游走进行图表征学习的基本思路，即如果两个点在各自的邻居范围内，那么它们的相似度就高。而邻居范围的定义则是通过一个策略 R R R获得的。
随机游走算法
定义：
- 在图 G ( V , E ) G(V, E) G(V,E)中，学习一种映射 z : u → R d \mathrm{z}: u \to \mathbb{R}^d z:u→Rd，目标是获取最大化的对数似然。 max z ∑ u ∈ V l o g P ( N R ( u ) ∣ z u ) \max_{z}\displaystyle\sum_{u\in V}\mathrm{logP}(N_R(u)|\mathrm{z}_u) zmaxu∈V∑logP(NR(u)∣zu)
其中， N R ( u ) N_R(u) NR(u)是通过策略 R R R获得的 u u u的邻居范围内的节点。
损失函数： L = ∑ u ∈ V ∑ v ∈ N R ( u ) − l o g ( P ( v ∣ z u ) ) \mathcal{L} = \displaystyle\sum_{u\in V}\sum_{v \in N_R(u)}-log(P(v|z_u)) L=u∈V∑v∈NR(u)∑−log(P(v∣zu))
这里通过取负数，把求最大值变成了求最小值，且是对所有的节点都进行随机游走并计算相似概率。
参数化的相似函数： P ( v ∣ z u ) = e x p ( z u ⊤ z v ) ∑ n ∈ V e x p ( z u ⊤ z n ) P(v|z_u)=\frac{\mathrm{exp}(\mathrm{z}_u^{\top}\mathrm{z}_v)}{\sum_{n\in V}\mathrm{exp}(\mathrm{z}_u^{\top}\mathrm{z}_n)} P(v∣zu)=∑n∈Vexp(zu⊤zn)exp(zu⊤zv)
上面两个公式合在一起，就是：
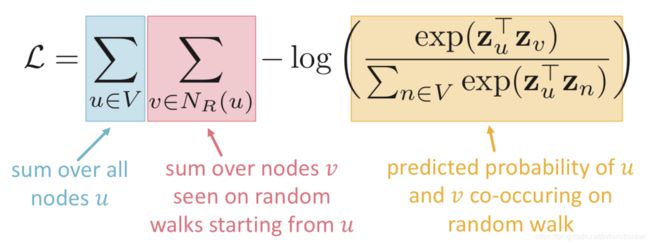
问题：分母上需要计算所有的边，这个就变成了 V 2 V^2 V2的计算量。所以需要新的方法。
负采样
上述的问题在word2vec的方法里也出现了，word2vec采用的负采样的方法在这里也适合。即从所有的节点里随机的选择一部分（ k k k个节点）作为负样本，同时把上面的相似函数进行变换。
P ( v ∣ z u ) = e x p ( z u ⊤ z v ) ∑ n ∈ V e x p ( z u ⊤ z n ) ≈ l o g ( σ ( z u ⊤ z v ) ) − ∑ i = 1 k l o g ( σ ( z u ⊤ z i ) ) P(v|z_u)=\frac{\mathrm{exp}(\mathrm{z}_u^{\top}\mathrm{z}_v)}{\sum_{n\in V}\mathrm{exp}(\mathrm{z}_u^{\top}\mathrm{z}_n)} \approx log(\sigma(\mathrm{z}_u^{\top}\mathrm{z}_v)) - \displaystyle\sum_{i=1}^klog(\sigma(\mathrm{z}_u^{\top}\mathrm{z}_i)) P(v∣zu)=∑n∈Vexp(zu⊤zn)exp(zu⊤zv)≈log(σ(zu⊤zv))−i=1∑klog(σ(zu⊤zi))
其中， n i ∼ P V n_i \sim P_V ni∼PV， P V P_V PV是对所有节点的随机分布。 σ \sigma σ是 s i g m o i d \mathrm{sigmoid} sigmoid函数。
选取 k k k的原则：
- 根据节点 u u u的度，按比例选择；
- 通常选5-20。
策略 R R R的选择
上讲述的都是如何选择相似度计算，而没有提到策略 R R R的细节。下面会介绍不同的策略。
固定长度随机游走：
选择一个固定的游走距离，非偏地选择邻居，完成游走。这也是最初的DeepWalk论文里使用的方法。
缺点：
用这种策略选择的节点，受限于长度，不能很好地表示距离较远但网络结构类型相似的节点的相似性。
Node2Vec算法
基本思想：
使用固定长度的、带偏的、2阶随机游走策略来获取点的邻居。其含义是在一个节点的看到的局部和全局的结构之间获取一个平衡。
基本做法：
利用BFS和DFS这两种遍历方式来表示获取局部和全局邻居信息的方法。
数学定义：
设置2个参数：
- 回退参数 p p p：返回到之前的节点的概率；
- 进-出参数 q q q：出(DFS，远离之前的节点)和入(BFS，之前节点的邻居)的比例关系。
通过这两个参数，就可以确定随机游走的可能的方向和下一个目标的点。如下图所示：
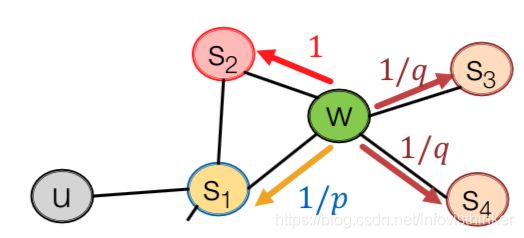如果想获得BFS类型的邻居，则使用更小的 p p p；想获得DFS类型的邻居，则使用更小的 q q q。每个节点上，游走的概率就是有偏的，分别是 1 / p , 1 , 1 / q , 1 / q , . . . 1/p, 1, 1/q, 1/q, ... 1/p,1,1/q,1/q,...。
算法细节：
- 对每个点计算游走概率；
- 固定序列长度 l l l，对每个节点 u u u，模拟随机游走的序列 r r r；
- 使用随机梯度下降更新node2vec的目标函数，从而获取点向量。
不同的 p p p和 q q q的设置会获取不同类型的embedding。
优点：上面的过程对每个点都是独立的，所以可以完全并行进行，保证是线性扩展的。
TransE构建知识图谱的点向量算法
图向量表征的一个经典的应用就是知识图谱，其中的一个早期经典的算法是Translating Embedding。
知识图谱
知识图谱是由事实和主张实体及其相互间的关系构成的图。其中实体是节点，关系是边。一般会用三元组来表示：头 h h h，关系 l l l， 尾 t t t → ( h , l , t ) \to (h, l, t) →(h,l,t)
知识图谱里常见的任务就是链接补全和链接更正(Link Prediction)，这可以帮助提升知识图谱的有效应用。
基本思路：
不仅在向量空间里两个相似的点距离要近，同时在向量空间里加上边的向量后，应该能指向到目标。
首先，实体(点)被编码到向量空间 R k R^k Rk，这一步和之前DeepWalk和Node2Vec的向量编码类似。
随后，关系要被编码成“翻译”，对于 h + l ≈ t h + l \approx t h+l≈t如果知识图谱里的三元组存在，否者就是 h + l ≠ t h + l \ne t h+l=t。
算法流程：
算法的核心是最后部分的比较损失函数，或者叫边际损失函数。它的通用形式是： L ( h , r , t ) = m a x ( 0 , f r ( h , t ) p o s − f r ( h , t ) n e g + m a r g i n ) L(h, r, t) = max(0, f_r(h, t)_{pos} - f_r(h, t)_{neg} + margin) L(h,r,t)=max(0,fr(h,t)pos−fr(h,t)neg+margin)
TransE的里的 f r ( h , t ) = ∣ ∣ h + r − t ∣ ∣ f_r(h, t) = ||h + r - t|| fr(h,t)=∣∣h+r−t∣∣，也就是上面图里的 d ( h + l , t ) d(h+l, t) d(h+l,t)。
整图向量编码
除了对于图中的点和边进行密集向量化编码，在一些场景里需要对整个图进行向量化，如化工制药里的分子图等。课程里一共介绍了3种方法。
方法1：简单求和
- 先对整图做标准的向量化；
- 然后对一个整图里所有的点的向量进行简单求和(或平均)。
Duvenaud et al., 2016
方法2：虚拟点
- 向一个整图引入一个“虚拟点”来代表这个图；
- 再对这个图做标准的向量化，再用这个“虚拟点”来表征整图。
Li et al., 2016
方法3：匿名游走
使用随机游走的方法，但是并不记忆具体游走的节点，而是记录游走节点和起始点对应的距离，并形成游走的记录。这个记录（对于图中所有的节点）会随着游走长度的增加而指数增加。
获得所有的随机游走记录后，可以使用3种方法进行整图向量化。
方法1: 所有游走的概率分布
- 遍历出某个固定长度的所有可能的匿名游走；
- 获取这些游走的概率分布，并用这个分布来表征整图。
方法2: 采样部分游走的概率分布
- 对于一些稍大的整图，遍历出所有的游走代价很大，这时候，采样 m m m个匿名游走；
- 用这些采样的概率分布来近似整体分布，并表征。
需要采样的个数： m = ⌈ 2 ε 2 ( l o g ( 2 η − 2 ) − l o g ( δ ) ) ⌉ m = \lceil \frac{2}{\varepsilon^2}(log(2^{\eta}-2)-log(\delta))\rceil m=⌈ε22(log(2η−2)−log(δ))⌉，其中 ε \varepsilon ε是错误率， δ \delta δ是错误率要低于的阈值， η \eta η是长度为 l l l的匿名游走的总数量。
方法3:学习每个游走的向量，再聚合
- 对每个匿名游走，学习出它则表征向量；
- 在把这些游走的表征向量进行聚合(求和、平均、叠加)来表征整图。
学习的方法没细讲。见原论文Anonymous Walk Embedding