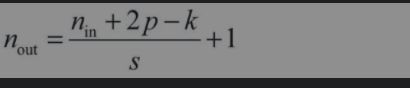Pytorch 目标检测学习 Day 2
1.网络骨架:Backbone
当前的物体检测算法虽然各不相同,但第一步通常是利用卷积神经网络处理输入图像,生成深层的特征图,然后再利用各种算法完成区域生成与损失计算,这部分卷积神经网络是整个检测算法的“骨架”,也被称为Backbone。
常用骨架:VGGNet :走向深度,Inception:纵横交错,ResNet:残差结构
DenseNet:多重残差,FPN:特征金字塔,DetNet:专为检测。
2.神经网络基本组成
物体检测算法使用的通常是包含卷积计算且具有深度结构的前馈神经网络,如卷积层、池化层、全连接层等不同的基本层,这些层有着不同的作用。
当然激活层对于Sigmoidbingbuc并不常用,较为常用的为ReLU()
2.1 卷积运算
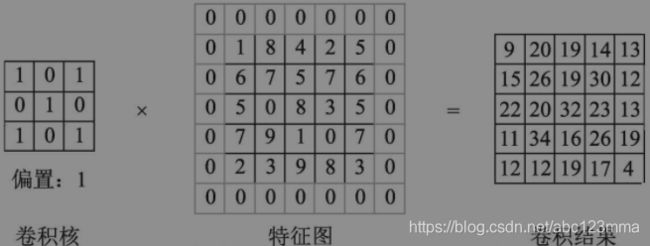
一个基本二维卷积的运算过程,公式为y=ωx+b。这里的特征图(x)大小为1×5×5,即输入通道数为1,卷积核(ω)的大小为3×3,偏置(b)为1,为保证输出维度和输入特征维度一致,还需要有填充(padding),这里使用zero-padding,即用0来填充。
通过用Pytorch 进行卷积代码编写
torch.nn.Conv2d()来说,传入参数含义如下
in_channels:输入特征图的通道数,如果是RGB图像,则通道数为3。卷积中的特征图通道数一般是2的整数次幂。
out_channels:输出特征图的通道数。
stride:步长,即卷积核在特征图上滑动的步长,一般为1。如果大于1,则输出特征图的尺寸会小于输入特征图的尺寸
padding:填充,常见的有零填充、边缘填充等,PyTorch默认为零填充。
dilation:空洞卷积,当大于1时可以增大感受野的同时保持特征图的尺寸(后面会细讲),默认为1。
groups:可实现组卷积,即在卷积操作时不是逐点卷积,而是将输入通道分为多个组,稀疏连接达到降低计算量的目的(后续会细讲),默认为1。
bias:是否需要偏置,默认为True。
在实际使用中,特征图的维度通常都不是1,假设输入特征图维度为m×win×hin,输出特征图维度为n×wout×hout,则卷积核的维度为n×m×k×k,在此产生的乘法操作次数为n×wout×hout×m×k×k。(计算复杂度)
2.2激活函数层
神经网络如果仅仅是由线性的卷积运算堆叠组成,则其无法形成复杂的表达空间,也就很难提取出高语义的信息,因此还需要加入非线性的映射,又称为激活函数,可以逼近任意的非线性函数,以提升整个神经网络的表达能力。在物体检测任务中,常用的激活函数有Sigmoid、ReLU及Softmax函数。
1.ReLU函数
为了缓解梯度消失现象,修正线性单元(Rectified LinearUnit, ReLU)被引入到神经网络中。由于其优越的性能与简单优雅的实现,ReLU已经成为目前卷积神经网络中最为常用的激活函数之一。ReLU函数的表达式如式(3-2)所示。[插图]ReLU函数及其梯度曲线如图3.5所示。可以看出,在小于0的部分,值与梯度皆为0,而在大于0的部分中导数保持为1,避免了Sigmoid函数中梯度接近于0导致的梯度消失问题。
2.Softmax 函数
多物体类别较为常用的分类器是Softmax函数
在具体的分类任务中,Softmax函数的输入往往是多个类别的得分,输出则是每一个类别对应的概率,所有类别的概率取值都在0~1之间,且和为1。Softmax函数的表达如式(3-4)所示,其中,Vi表示第i个类别的得分,C代表分类的类别总数,输出Si为第i个类别的概率
3.池化层
在卷积网络中,通常会在卷积层之间增加池化(Pooling)层,以降低特征图的参数量,提升计算速度,增加感受野,是一种降采样操作。池化是一种较强的先验,可以使模型更关注全局特征而非局部出现的位置,这种降维的过程可以保留一些重要的特征信息,提升容错能力,并且还能在一定程度上起到防止过拟合的作用。
在物体检测中,常用的池化有最大值池化(Max Pooling)与平均值池化(Average Pooling)。池化层有两个主要的输入参数,即核尺寸kernel_size与步长stride。如图3.7所示为一个核尺寸与步长都为2的最大值池化过程,以左上角为例,9、20、15与26进行最大值池化,保留26。
4.Dropout层
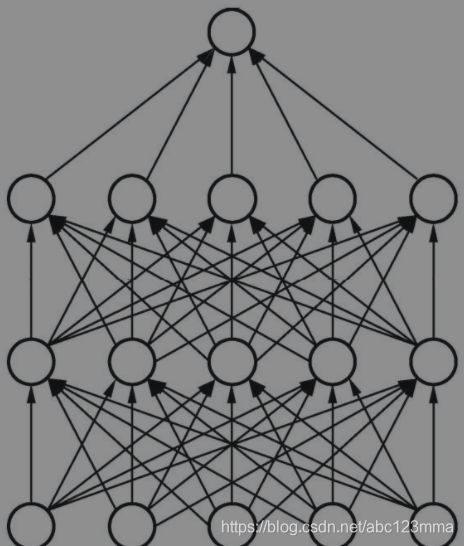
Dropout的基本思想如图3.8所示,在训练时,每个神经元以概率p保留,即以1-p的概率停止工作,每次前向传播保留下来的神经元都不同,这样可以使得模型不太依赖于某些局部特征,泛化性能更强。
在测试时,为了保证相同的输出期望值,每个参数还要乘以p。当然还有另外一种计算方式称为Inverted Dropout,即在训练时将保留下的神经元乘以1/p,这样测试时就不需要再改变权重。
为什么Dropout可以防止过拟合,
1.多模型的平均:不同的固定神经网络会有不同的过拟合,多个取平均则有可能让一些相反的拟合抵消掉,而Dropout每次都是不同的神经元失活,可以看做是多个模型的平均,类似于多数投票取胜的策略。
2.减少神经元间的依赖:由于两个神经元不一定同时有效,因此减少了特征之间的依赖,迫使网络学习有更为鲁棒的特征,因为神经网络不应该对特定的特征敏感,而应该从众多特征中学习更为共同的规律,这也起到了正则化的效果。
3.生物进化:Dropout类似于性别在生物进化中的角色,物种为了适应环境变化,在繁衍时取雄性和雌性的各一半基因进行组合,这样可以适应更复杂的新环境,避免了单一基因的过拟合,当环境发生变化时也不至于灭绝。
5.BN层
BN层首先对每一个batch的输入特征进行白化操作,即去均值方差过程。假设一个batch的输入数据为x:B={x1, …,xm},首先求该batch数据的均值与方差,如式(3-5)和式(3-6)所示。
为批处理数据的方差。在求得均值方差后,利用式(3-7)进行去均值方差操作:
化操作可以使输入的特征分布具有相同的均值与方差,固定了每一层的输入分布,从而加速网络的收敛。
但也限制了网络中数据的表达能力,浅层学到的参数信息会被白化操作屏蔽掉,因此,BN层在白化操作后又增加了一个线性变换操作,让数据尽可能地恢复本身的表达能力
- ·由于是在batch的维度进行归一化,BN层要求较大的batch才能有效地工作,而物体检测等任务由于占用内存较高,限制了batch的大小,这会限制BN层有效地发挥归一化功能。
- ·数据的batch大小在训练与测试时往往不一样。在训练时一般采用滑动来计算平均值与方差,在测试时直接拿训练集的平均值与方差来使用。这种方式会导致测试集依赖于训练集,然而有时训练集与测试集的数据分布并不一致。
6.全连接层
全连接层(Fully Connected Layers)一般连接到卷积网络输出的特征图后边,特点是每一个节点都与上下层的所有节点相连,输入与输出都被延展成一维向量,因此从参数量来看全连接层的参数量是最多的,
在物体检测算法中,卷积网络的主要作用是从局部到整体地提取图像的特征,而全连接层则用来将卷积抽象出的特征图进一步映射到特定维度的标签空间,以求取损失或者输出预测结果。
点缺:
全连接层的缺点也逐渐暴露了出来,最致命的问题在于其参数量的庞大
解决方案:
我们可以使用全局平均池化层(Global AveragePooling,GAP)来取代全连接层,这种思想最早见于NIN(Network in Network)网络中,总体上,使用GAP有如下3点好处:
- ·利用池化实现了降维,极大地减少了网络的参数量。
- ·将特征提取与分类合二为一,一定程度上可以防止过拟合。
- ·由于去除了全连接层,可以实现任意图像尺度的输入。
7.深入理解感受野(FPN)
感受野(Receptive Field)是指特征图上的某个点能看到的输入图像的区域,即特征图上的点是由输入图像中感受野大小区域的计算得到的。
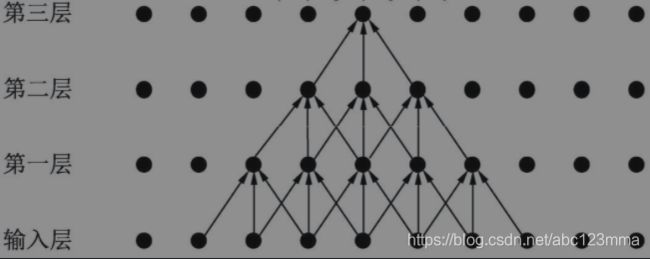
举个简单的例子,如图3.10所示为一个三层卷积网络,每一层的卷积核为3×3,步长为1,可以看到第一层对应的感受野是3×3,第二层是5×5,第三层则是7×7。
可以形象说明:为什么后来的卷积都用3*3核代替5*5或者7*7的卷积核
卷积层和池化层都会影响感受野,而激活函数层通常对于感受野没有影响。对于一般的卷积神经网络,感受野。
其中,RFl+1与RFl分别代表第l+1层与第l层的感受野,k代表第l+1层卷积核的大小,Sl代表前l层的步长之积。注意,当前层的步长并不影响当前层的感受野。
通过上述公式求取出的感受野通常很大,而实际的有效感受野(Effective Receptive Field)往往小于理论感受野。从上图也可以看出,虽然第三层的感受野是7×7,但是输入层中边缘点的使用次数明显比中间点要少,因此做出的贡献不同。经过多层的卷积堆叠之后,输入层对于特征图点做出的贡献分布呈高斯分布形状。
在卷积网络中,有时还需要计算特征图的大小,一般可以按照下图进行计算。
其中,nin与nout分别为输入特征图与输出特征图的尺寸,p代表这一层的padding大小,k代表这一层的卷积核大小,s为步长。
8.详解空洞卷积(Dilated Convolution)
空洞卷积最初是为解决图像分割的问题而提出的。常见的图像分割算法通常使用池化层来增大感受野,同时也缩小了特征图尺寸,然后再利用上采样还原图像尺寸。特征图缩小再放大的过程造成了精度上的损失,因此需要有一种操作可以在增加感受野的同时保持特征图的尺寸不变,从而替代池化与上采样操作,在这种需求下,空洞卷积就诞生了。
空洞卷积,顾名思义就是卷积核中间带有一些洞,跳过一些元素进行卷积。
图3.11a是普通的卷积过程,在卷积核紧密排列在特征图上滑动计算,而图3.11b代表了空洞数为2的空洞卷积,可以看到,在特征图上每2行或者2列选取元素与卷积核卷积。类似地,图3.11c代表了空洞数为3的空洞卷积。
图3.11 普通卷积与空洞卷积的对比
在代码实现时,空洞卷积有一个额外的超参数dilationrate,表示空洞数,普通卷积dilation rate默认为1,图3.11中的b与c的dilation rate分别为2与3。
在图3.11中,同样的一个3×3卷积,却可以起到5×5、7×7等卷积的效果。可以看出,空洞卷积在不增加参数量的前提下,增大了感受野。假设空洞卷积的卷积核大小为k,空洞数为d,则其等效卷积核大小k’计算如式(3-12)所示。
缺点:
- ·网格效应(Gridding Effect):由于空洞卷积是一种稀疏的采样方式,当多个空洞卷积叠加时,有些像素根本没有被利用到,会损失信息的连续性与相关性,进而影响分割、检测等要求较高的任务。
- ·远距离的信息没有相关性:空洞卷积采取了稀疏的采样方式,导致远距离卷积得到的结果之间缺乏相关性,进而影响分类的结果。
- ·不同尺度物体的关系:大的dilation rate对于大物体分割与检测有利,但是对于小物体则有弊无利,如何处理好多尺度问题的检测,是空洞卷积设计的重点。