多元统计分析及R语言建模（第五版）——第4章 多元相关与线性回归分析课后习题
第4章 多元相关与线性回归分析
本文用到的数据可以去这个网址下下载多元统计分析及R语言建模（第5版）数据
练习题
1）一家保险公司想了解其总公司营业部加班时间与签发的新保单数目之间的关系，经过10周时间，收集了每周加班工作时间x（小时）和签发的新保单数目y的数据（张），…
(1)绘制散点图，并以此判断x与y之间是否大致呈线性关系
x = c(3.5,1,4,2,1,3,4.5,1.5,3,5)
y = c(825,215,1070,550,480,920,1350,325,670,1215)
z = data.frame(x,y)
z
plot(x,y,main = '散点图',xlab = '每周加班时间（小时）',ylab = '每周签发的新保单数目（张）') #绘制散点图
根据散点图可知，x与y之间大致呈线性关系
（2）计算x与y的相关系数
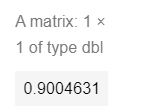
cor(x,y) #计算相关系数，相关系数计算函数cor()
（3）用最小二乘估计法求回归方程
lm4.1 <- lm(y ~ x)
lm4.1
由结果可知回归方程为：y = 251.17x + 46.15
（4）求随机误差ε的方差σ^2的估计值
x_hat <- 46.15 + 251.17*x
square_sigma <- t(x_hat - y)%*%(x_hat - y)/(10-1-1)
square_sigma
(summary(lm4.1) $ sigma)^2
（5）计算x与y的决定系数
SSR <- t(x_hat - mean(y))%*%(x_hat - mean(y))
SST <- t(y - mean(y))%*%(y - mean(y))
square_R <- SSR / SST
square_R
(summary(lm4.1) $ r.squared)
（6）对回归方程作方差分析
anova(lm4.1)
由于P<0.05，于是在α=0.05水平处拒绝H0，接受H1，即本例回归系数有统计意义，x与y间存在直线回归关系
（7）对回归方程作残差图并做一些分析
res <- residuals(lm4.1)
res
plot(x,res,main='残差散点图',xlab='每周签发的新保单数目',ylab='残差')
（8）计算y0 = 1000(张)需要的加班时间是多少？
plot(lm4.1)
lm4.1_1 <- lm(y ~ x,data = z)
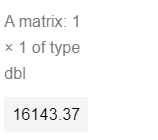
predict(lm4.1_1,newdata = data.frame(y = 1000))
lxy <- function(x1,y1){
n = length(x1)
sum(x1*y1) -sum(x1)*sum(y1)/n}
a = lxy(x,y)/lxy(x,x) #线性回归方程斜率
b = mean(y) - b*mean(x) #线性回归方程截距
y0 = 1000
x0 = (y0 - b)/a
x0
2)某家房地产公司的总裁想了解为什么公司中的某些分公司比其他公司表现出色，他认为决定总年销售额（以百万元计）的关键因素是广告预算（以千元计）和销售代理的数目。为了分析这种情况，他抽取了8家公司作为样本，…
(1)试做回归模型并解释各系数
library(openxlsx)
d4.2 = read.xlsx('mvexer5.xlsx',sheet = 'E4.5',rowNames = T)
(lm4.2 = lm(y ~ x1 + x2,data = d4.2)) #显示多元线性回归模型
多元线性方程：y = -22.75 + 0.1511 x1 + 1.22 x2 ;
coef.sd <- function(lm4.2){
#标准回归系数
b = lm4.2 $ coef
b
si = apply(lm4.2 $ model,2,sd)
si
bs = b[-1] * si[-1]/si[1]
bs
}
coef.sd(lm4.2)
标准化偏回归系数为
x1：0.474129333891668
x2：0.330013256080993，
由标准化偏回归系数可见，广告预算和销售代理的数目对年销售额的线性影响还是挺大的
(2）在5%的显著水平下确定每一解释变量与依赖变量是否呈线性关系
summary(lm4.2)
P=0.2412>α=0.05，所以接受原假设H0,说明x与y没有显著的线性关系
（3）计算简单相关系数和复相关系数
cor(d4.2) #多元数据相关系数矩阵
(R2 = summary(lm4.2) $ r.sq)
(R_2 = sqrt(R2)) #计算复相关系数
3)要了解学校毕业生起始工资的变化是否能用学生的平均成绩点数（GPA）和毕业时的年龄来解释，…
(1)试做回归模型并解释各系数
library(openxlsx)
d4.3 =read.xlsx('mvexer5.xlsx',sheet = 'E4.3')
(lm4.3 = lm(起始工资~ GPA + 年龄,data = d4.3))
多元线性回归函数：起始工资 = -5213.1 + 8508.8 GPA + 181.6
年龄 在GPA不变的情况下，年龄增加一个单位，起始工资增加181.6个单位
在年龄不变的情况下，GPA增加一个单位，起始工资增加8508.8个单位
(2）确定学生的GPA和年龄是否能真正用来解释起始工资样本的变化
summary(lm4.3)
R^2=Multiple R-squared=0.0.1803不接近1,说明回归方程拟合度低，学生的GPA和年龄不能真正用来解释起始工资样本的变化
(R4.3 = summary(lm4.3) $ r.sq)
(R_2_4.3 = sqrt(R4.3))
(3)预测某GPA为3.00，年龄为24岁的毕业生的起始工资
predict(lm4.3,newdata = data.frame(GPA = 3,年龄 = 24))
4)研究货运总量y（万吨）与工业总产值x1（亿元）、农业总产值x2（亿元）、居民非商品支出x3(亿元)的关系，…
(1)计算y,x1,x2,x3的相关系数矩阵并绘制矩阵散点图
library(openxlsx)
d4.4 = read.xlsx('mvexer5.xlsx',sheet = 'E4.4')
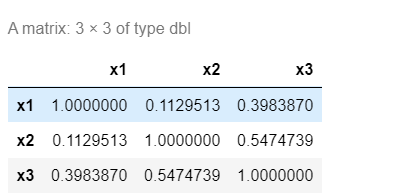
cor4.4 <- cor(d4.4[,-1]) #去除第一列编号数据后剩余的样本计算相关系数矩阵
cor4.4
pairs(d4.4) #绘制矩阵散点图
(2）求y关于x1,x2,x3的多元线性回归方程
lm4.4 <- lm(y ~ x1 + x2 + x3,data = d4.4) #建立回归方程
summary(lm4.4)
得到y = -348.280+3.754x1+7.101x2+12.447X3
（3）对所求得的方程做拟合优度检验
summary(lm4.4)
R^2=Multiple R-squared=0.8055接近1,说明回归方程拟合度高
(R4.4 = summary(lm4.4)$r.sq)
R^2=Multiple R-squared=0.8055接近1,说明回归方程拟合度高
(R_2_4.4 = sqrt(R4.4))
R=0.8974965>R0.05(8)=0.632，所以接受原假设，说明x与y有显著的线性关系
（4）对回归方程做显著性检验，对每一个回归系数做显著性检验
summary(lm4.4)
P=0.01487<α=0.05，所以拒绝原假设H0,说明x与y有显著的线性关系
（5）如果有的回归系数没通过显著性检验，将其剔除，重新建立回归方程，再做回归方程的显著性检验和回归系数的显著性检验
lm4.4_drop3 <- lm(y ~ x1 + x2,data = d4.4)
lm4.4_drop3
P3=0.2835最大，剔除x3，建立新的回归方程 summary(lm3.11_drop3) #自己先简单用summary函数看新的回归方程是否符合检验，再用F跟t检验最终方程（方便点） 此时P1=0.03676<α=0.05，P2=0.00835<α=0.05，所有的自变量在显著性水平α=0.05时都显著
重新建立回归方程y=-459.624+4.676x1+8.971x2 对新的回归方程做显著性检验。 提出原假设H0=β1=β2=0
summary(lm4.4_drop3)
P=0.006718<α=0.05，所以拒绝原假设H0,说明x与y有显著的线性关系
#对每一个回归系数做显著性检验
summary(lm4.4_drop3)
t1 <- 1.942
t2 <- 2.465
t3 <- 1.178
qt(1-0.05,7)
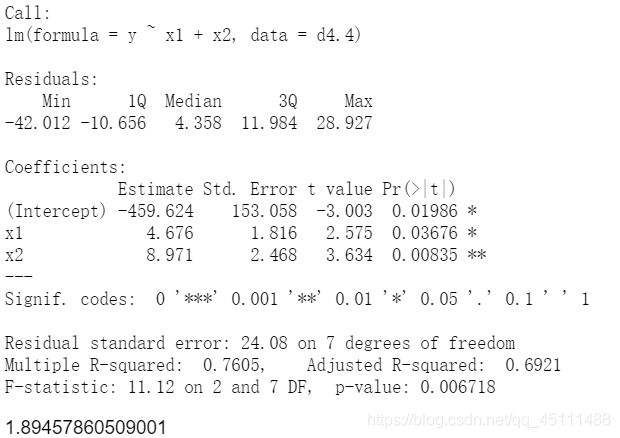
t值~tα(n-p-1) #t0.05(7)=1.895 t1=2.575>t0.05(7)=1.895，P1=0.03676<α=0.05，所以拒绝原假设，说明x1对y有显著的影响 t2=3.634>t0.05(7)=1.895，P2=0.00835<α=0.05，所以拒绝原假设，说明x2对y有显著的影响
得到最终回归方程y=-459.624+4.676x1+8.971x2
（6）使用逐步回归分析的逐步筛选方法获得一个最优的回归模型
lm.step = step(lm4.4,direction = 'forward') #向前引入法变量选择结果
lm.step = step(lm4.4,direction = 'backward') #向后剔除法变量选择结果
lm.step = step(lm4.4,direction = 'both') #逐步筛选法变量选择结果
