基于启发式策略的图着色问题
目录
- 问题背景
- 解决思路
- 代码实现
- 说明
问题背景
图着色问题（Graph Coloring Problem, GCP） 又称着色问题，是最著名的NP-完全问题之一。道路着色问题（Road Coloring Problem）是图论中最著名的猜想之一。
数学定义：给定一个无向图G=（V, E），其中V为顶点集合，E为边集合，图着色问题即为将V分为K个颜色组，每个组形成一个独立集，即其中没有相邻的顶点。其优化版本是希望获得最小的K值。
人类已经用计算机证明，一切平面可着色图，都可用4种颜色以内进行涂色。本实验不作任何理论证明，只提供一个可以解决问题的思路和代码实现方式。
解决思路
- 对于解决如何用K种颜色完成涂色过程，我采用回溯法遍历搜索。如果能够在搜索和回溯过程中找到一个解，则该问题解决；如果遍历完所有的情况，则可认为该问题无解。
- 对于解决如何找到K的最小值，可以将K在一定范围内依次尝试。如果能找到用m种颜色成功，而用m - 1种颜色失败，则可以认为 K = m。
- 对于1中的回溯法遍历搜索，如果采取无信息搜索，效率低下，故引入启发式策略，分别为：（1）当前状态下，值域最小的顶点优先被涂色；（2）值域大小相同者，度最大者优先。引入该方法，解决复杂的图着色问题，效率会大大提高。
代码实现
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
import functools
# 邻接矩阵
Matrix = np.array([
[0, 1, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 1, 1],
[0, 1, 0, 1, 1, 0, 1],
[1 ,1 ,1, 0, 1, 0, 0],
[0 ,1 ,1, 1, 0, 1, 1],
[0, 1, 0, 0, 1, 0, 0],
[1, 1, 1, 0, 1, 0, 0],])
G = nx.Graph(Matrix) # 用邻接矩阵建图
color_list = ['b','c','g','k','m', 'r','y'] # 颜色列表
max_color_num = 4 # 允许使用颜色的最大值
num = len(Matrix) # 顶点个数
class ColorProblem(object):
'''
有策略搜索 + 回溯
'''
def __init__(self):
self.path = []
self.visited = set()
self.color = 'w' * num
self.colored_num = 0
self.ok = False
for i in range(num):
if self.color[i] != 'w':
self.colored_num += 1
def cur_is_legle(self):
'''
判断当前状态是否合法
'''
for vi in range(num):
for vj in range(num):
if vi != vj and Matrix[vi][vj] and self.color[vi] != 'w' and self.color[vi] == self.color[vj]:
return False
return True
def is_legle(self,color_s:str):
'''
判断某一状态是否合法
'''
for vi in range(num):
for vj in range(num):
if vi != vj and Matrix[vi][vj] and color_s[vi] != 'w' and color_s[vi] == color_s[vj]:
return False
return True
def get_next(self):
'''
获得涂色方法，[i, j]表示将节点i涂为颜色j
'''
next = []
for i in range(num):
if self.color[i] != 'w':
continue
for j in range(max_color_num):
next_state = self.color
temp = list(next_state)
temp[i] = color_list[j]
next_state = ''.join(temp)
if next_state in self.visited or not self.is_legle(next_state):
continue
next.append((i,j))
def cmp(x,y):
'''
比较函数，其比较策略如下：
1.值域最小者优先
2.值域大小相同者，度最大者优先
'''
set_x = set() # 储存邻点的颜色，颜色多者值域小
set_y = set()
for i in range(num):
if Matrix[x[0]][i] == 0:
continue
if self.color[i] == 'w':
continue
set_x.add(self.color[i])
for i in range(num):
if Matrix[x[0]][i] == 0:
continue
if self.color[i] == 'w':
continue
set_y.add(self.color[i])
if len(set_x) > len(set_y): # 值域小优先
return 1
if len(set_x) < len(set_y):
return -1
if G.degree(x[0]) > G.degree(y[0]): # 度启发式
return 1
if G.degree(x[0]) < G.degree(y[0]):
return -1
return 0
# 根据上述策略，对涂色可能的策略表进行排序
next.sort(key=functools.cmp_to_key(cmp),reverse=True)
if len(next):
return next[0]
return None
def go_next(self):
'''
涂色以转化为下一状态
'''
next = self.get_next()
if next == None:
return False
next_state = list(self.color)
next_state[next[0]] = color_list[next[1]]
self.color = ''.join(next_state)
self.path.append(next)
self.visited.add(self.color)
self.colored_num+=1
self.display()
if not self.cur_is_legle():
return False
if self.colored_num == num:
self.ok = True
return True
def go_back(self):
'''
回溯
'''
back = self.path.pop()
self.colored_num -= 1
temp = list(self.color)
temp[back[0]] = 'w'
self.color = ''.join(temp)
self.display()
def start_color(self):
'''
开始涂色
'''
if self.go_next() == False:
return
while self.color != 'w' * num and self.ok == False:
if not self.go_next():
self.go_back()
if self.ok:
self.display()
print(self.color)
return
print("There's no legal solution!")
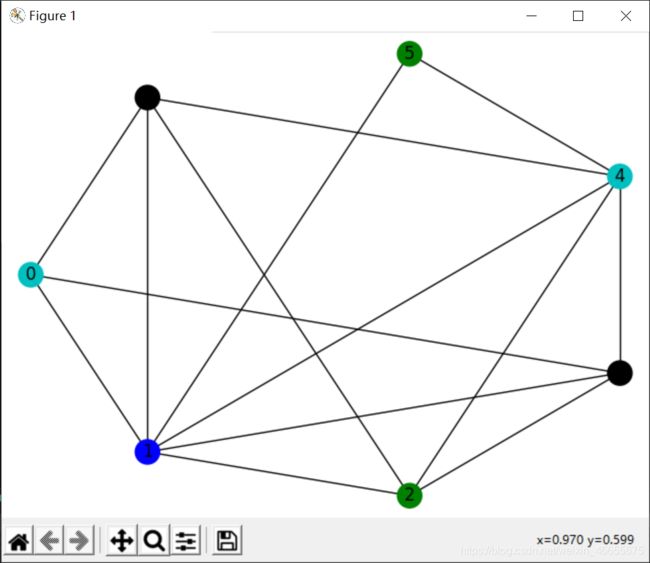
def display(self):
plt.clf()
nx.draw_shell(G, with_labels=True, node_color=list(self.color))
plt.pause(0.02)
if __name__ == '__main__':
plt.figure()
plt.ion()
p = ColorProblem()
p.start_color()
plt.ioff()
plt.show()
说明
- 本代码采取的是带启发式的回朔法，类似于贪婪算法+深度优先的策略。可以尝试改变
max_color_num的值确定最小的颜色种类。 - 本算法完备性好，理论上是比无信息回溯更加高效的。但是其高效与否，有待于更大更丰富的、不同规模的测试集去验证。如果感兴趣，可以用如下最初不带启发式策略的方法进行对比。（但是注意要调整动画效果，取消暂停。）代码也贴上：
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
import functools
# 邻接矩阵
Matrix = np.array([
[0, 1, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 1, 1],
[0, 1, 0, 1, 1, 0, 1],
[1 ,1 ,1, 0, 1, 0, 0],
[0 ,1 ,1, 1, 0, 1, 1],
[0, 1, 0, 0, 1, 0, 0],
[1, 1, 1, 0, 1, 0, 0],])
G = nx.Graph(Matrix) # 用邻接矩阵建图
color_list = ['b','c','g','k','m', 'r','y'] # 颜色列表
max_color_num = 4 # 允许使用颜色的最大值
num = len(Matrix) # 顶点个数
class ColorProblem(object):
'''
无启发式，暴力回溯
'''
def __init__(self):
self.path = []
self.visited = set()
self.color = 'w' * num
self.colored_num = 0
self.ok = False
# 用白色将各个顶点初始化
for i in range(num):
if self.color[i] != 'w':
self.colored_num += 1
def is_legle(self):
'''
判断合法性
'''
for vi in range(num):
for vj in range(num):
if vi != vj and Matrix[vi][vj] and self.color[vi] != 'w' and self.color[vi] == self.color[vj]:
return False
return True
def get_next(self):
'''
获得涂色方法，[i, j]表示将节点i涂为颜色j
'''
next = []
for i in range(num):
if self.color[i] != 'w':
continue
for j in range(max_color_num):
next_state = self.color
temp = list(next_state)
temp[i] = color_list[j]
next_state = ''.join(temp)
if next_state not in self.visited:
next.append((i,j))
'''
此处可以优化
'''
if len(next):
return next[0]
return None
def go_next(self):
'''
涂色，变为下一状态
'''
next = self.get_next()
if next == None:
return False
next_state = list(self.color)
next_state[next[0]] = color_list[next[1]]
self.color = ''.join(next_state)
self.path.append(next)
self.visited.add(self.color)
self.colored_num+=1
self.display()
if not self.is_legle():
return False
if self.colored_num == num:
self.ok = True
return True
def go_back(self):
'''
回溯
'''
back = self.path.pop()
self.colored_num -= 1
temp = list(self.color)
temp[back[0]] = 'w'
self.color = ''.join(temp)
self.display()
def start_color(self):
'''
开始涂色
'''
if self.go_next() == False:
return
while self.color != 'w' * num and self.ok == False:
if not self.go_next():
self.go_back()
if self.ok:
self.display()
print(self.color)
return
print("There's no legal solution!")
def display(self):
plt.clf()
nx.draw_shell(G, with_labels=True, node_color=list(self.color))
plt.pause(0.02)
if __name__ == '__main__':
plt.figure()
plt.ion()
p = ColorProblem()
p.start_color()
plt.ioff()
plt.show()
- 有没有能够只经过一次搜索而不需要回溯过程就可以用最少颜色完成的涂色方法？据我所知，无，但是有近似算法，即多数情况下可以通过不用回溯的方式，一步到位地涂完所有颜色。
可以参考这篇博客《着色近似算法——韦尔奇-鲍威尔（Welch-Powell）点着色算法》。 - 动画演示效果（最终图）
