【学习笔记】网络流基础（1）

网络流概念
网络流问题是图论中一类常见的问题。
许多系统都包含了流量，例如，公路系统中的车辆流，控制系统中的信息流，供水系统中有水流，金融系统中有现金流等等。
网络流是一个适用范围相当广的模型，相关的算法也非常多。
尽管如此，网络流中的概念、思想和基本算法并不难理解。
最大流问题
先看一个运输方案设计的例子。
图 (a) 是连接产品产地 V[s]（称为源点），和销售地 V[t]（称为汇点）的交通网，每一条弧 代表从 到 的运输线，产品经过这条弧由 u 输送到 v ，弧旁的数字表示这条运输线的最大通过能力（以后简称容量），单位为百吨。
产品经过交通网从 V[s] 输送到 V[t]。
现在要求制定一个运输方案，使得从 V[s] 运输到 V[t] 的产品数量最多。

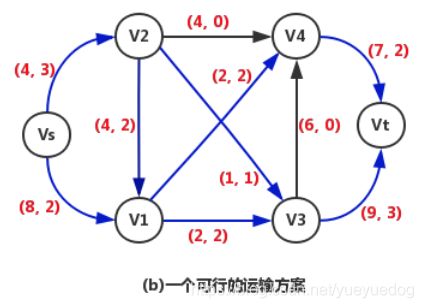
图 (b) 给出了一个可行的运输方案（粗线所表示的弧为运输方案中的弧）：
(1) 2 百吨物资沿着有向路径 P1(V[s], V[1], V[2], V[4], V[t]) 运到销售地；
(2) 2百吨物资沿着有向路径 P2(V[s], V[1], V[3], V[t]) 运到销售地；
(3) 1百吨物资沿着有向路径 P3(V[s], V[2], V[3], V[t]) 运到销售地。
总的运输量为 5 百吨。
在图 (b) 中，每条弧旁边的两个数字，如 (4, 3) ，分别代表弧的容量和实际运输量。
一个可行的运输方案应满足：
(1) 实际运输量不能是负的；
(2) 每条弧的实际运输量不能大于该弧的容量；
(3) 除了源点 V[s] 和汇点 V[t] 外，对其它顶点 u 来说，所有流入 u 的弧上的运输量总和应该等于所有从 u 出发的弧上的运输量总和。
现在的问题是：
(1) 从 V[s] 到 V[t] 的运输量是否可以增多？
(2) 从 V[s] 到 V[t] 的最大运输量是多少？
我们把这样的问题称为最大流问题。
在容量网络 G(V, E) 中，可行流 为满足如下条件的网络流：
弧流量限制条件：0 ≤ f(u, v) ≤ c(u, v), ∈ E
平衡条件：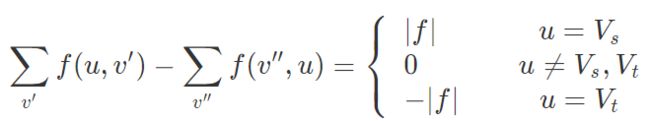

其中 ∑v’ f(u, v’) 是从顶点 u 流出的流量之和，∑v’’ f(v’’, u) 是流入顶点 u 的流量之和，|f| 是可行流的总流量，是源点的净流出量，也是汇点的净流入量。
对于任何一个容量网络，可行流总是存在的，如 f = 0，即每条弧上的流量为0，该网络流称为零流。
最大流是指容量网络 G(V, E) 中满足弧流量限制条件和平衡条件且具有最大流量的可行流。
EK算法
链与增广路
在容量网络 G(V, E) 中，设有一可行流 f = {f(u, v)}，根据每条弧上流量的
多少以及流量和容量的关系，可将弧分四种类型：
(1) 饱和弧：即 f(u, v) = c(u, v)；
(2) 非饱和弧：即 f(u, v) < c(u, v)；
(3) 零流弧：即 f(u, v) = 0；
(4) 非零流弧：即 f(u, v) > 0。
不难看出，饱和弧与非饱和弧，零流弧与非零流弧这两对概念是交错的，饱和弧一般也是非零流弧，零流弧一般也是非饱和弧。
链
在容量网络中，称顶点序列 u, u[1], u[2]…v 为一条链，要求相
邻两个顶点之间有一条弧，如 或 为容量网络中的一条弧。设 P 是 G 中从 V[s] 到 V[t] 的一条链，约定从 V[s] 指向 V[t] 的方向为该链的正方向。
注意，链的概念不等同于有向路径的概念，在链中，并不要求所有的弧都与链的正方向同向。
沿着 V[s] 到 V[t] 的一条链，各弧可分为两类：
(1) 前向弧（方向与链的正方向一致的弧），其集合记为P+；
(2) 后向弧（方向与链的正方向相反的弧），其集合记为P- 。
注意，前向弧和后向弧是相对的，即相对于指定链的正方向。
例如在图 (a) 中，指定的链为：P = {V[s], V[1], V[2], V[4], V[t]} ，这条链在图 (a)中用蓝线标明。
则 P+ 和 P- 分别为：
P+ = {, , }, P- = {}

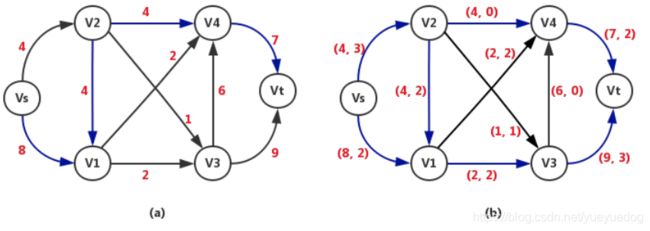
注意，同一条弧可能在某条链中是前向弧，而在另外一条链中是后向弧。
例如，如图 (b) 所示，弧 在链 P1 = {V[s], V[1], V[2], V[4], V[t]} 是后向弧，而在链 P2 = {V[s], V[2], V[1], V[3], V[t]} 是前向弧。
增广路
设 f 是一个容量网络 G 中的可行流，P 是从 V[s] 到 V[t] 的一条链，若 P 满足下列条件：
(1) 在 P 的所有前向弧 上，0 ≤ f(u, v) ≤ c(u, v)，即 P+ 中的每一条弧都是非饱和弧；
(2) 在 的所有后向弧 上，0 < f(u, v) ≤ c(u, v) ，即 P- 中每一条弧是非零流弧。
则称 P 为关于可行流 f 的一条增广路，简称为增广路。
那么，为什么将具有上述特征的链 P 称为增广路呢？
原因是可以通过修正 P 上所有弧的流量 f(u, v) 来把现有的可行流 f 改进成一个值更大的流 f1。
沿着增广路改进可行流的操作称为增广。
残量与残量网络
残量：给定容量网络 G(u, v) 及可行流 f，弧 上的残量记为 c(u, v) = c(u, v) - f(u, v)。
每条弧的残量表示该弧上可以增加的流量。
因为，从顶点 u 到顶点 v 流量的减少，等效于顶点 v 到顶点 u 流量增加，所以每条弧 上还有一个反方向的残量 。
残量网络：设有容量网络 G(V, E) 及其上的网络流 f，G 关于 f 的残量网络记为 G’(V’, E’)，其中 G’ 的顶点集 V’ 和 G 的顶点集 V 相同，即 V’ = V，对于 G 中的任何一条弧 ，如果 f(u, v) < c(u, v)那么在 G’ 中有一条弧 ∈E’，其容量为 c’(u, v) = c(u, v) - f(u, v)，如果 f(u, v) > 0，则在 G’ 中有一条弧 ∈E’，其容量为 c’(v, u) = f(u, v)。
从残量网络的定义可以看出，原容量网络中的每条弧在残量网络中都化为一条或两条弧。
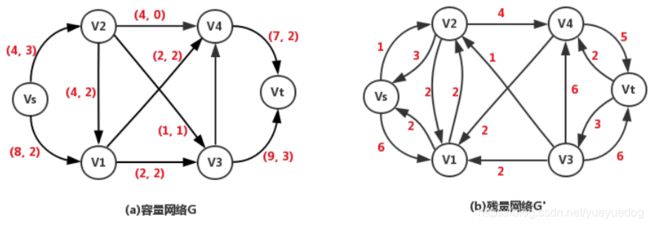
例如图 (a) 所示的容量网络 G ，其残量网络 G’ 为图 (b)。
残量网络中每条弧都表示在原容量网络中能沿其方向增广，弧 的容量表示原容量网络能沿着 u 到 v 的方向增广大小为 c’(u, v) 的流量。
因此，在残量网络中，从源点到汇点的任意一条简单路径都对应一条增广路，路径上每条弧容量的最小值即为能够一次增广的最大流量。
例如，在图 (b) 中，源点到汇点的一条路径为 (V[s], V[2], V[4], V[t]])，这条路径有 3 条弧，容量分别为 1、4 、5 ，因此沿着这条路径增广可以增加 个单位的流量。

残量网络与原网络的关系：设 f 是容量网络 G(V, E) 的可行流，f’ 是残量网络 G’ 的可行流，则 f + f’ 仍是容量网络 G 的一个可行流。（ f + f’表示对应弧上的流量相加）。
显然，只要残量网络中存在增广路，流量就可以增大。
可以证明它的逆命题也成立：如果残量网络中不存在增广路，则当前流就是最大流。
这就是著名的增广路定理。
找增广路的一个好的方法是使用 BFS，它足以应对数据不刁钻的网络流题目。
这就是最短增广路算法（Edmonds-Karp 算法，简称 EK 算法），即每次沿着最短增广路（即边数最少的增广路）进行增广。
算法的时间复杂度为： O(VE ^ 2)。
实现 EK 算法

#include 
#include 
#include 
#include 
using namespace std;
const int MAX_N = 200;
const int MAX_M = 400;
const int INF = 0x3f3f3f3f;
struct edge {
     
    int u, v, c, next;
} e[MAX_M];
int p[MAX_N], eid, S, T;
void init() {
     
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v, int c) {
     
    e[eid].u = u;
    e[eid].v = v;
    e[eid].c = c;
    e[eid].next = p[u];
    p[u] = eid++;
}
void addedge(int u, int v, int c) {
     
    insert(u, v, c);
    insert(v, u, 0);
}

Dinic 算法
与 EK 算法类似， Dinic 算法也是不停的寻找增广路。不同之处有两个地方

1. 构建分层图，按照层次关系增广。具体地，对源点进行 BFS，对每个节点按照层次编号，我们增广的时候，流量只会从低层次的节点往高层次的节点走，而不会出现回流的情况。也就是按照最短路进行增广。
2. DFS 进行多路增广。 EK 算法一次只会增广一条路径， Dinic 通过 DFS 能同时找到多条广路。
   通过上面两个优化， Dinic 算法的时间效率大大的提升。
   Dinic 算法的基本步骤
3. 初始化网络和网络流。
4. 构造剩余网络和层次网络，若汇点不在层次网络中则算法结束。
5. 在层次图 G ^ L 内用一次 DFS 过程进行增广，DFS 执行完毕则该阶段增广完
   毕。
6. 转步骤2 。
   算法实例
   
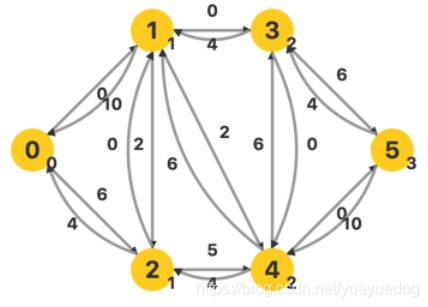
   在如上的网络中，源点为 0，汇点为 5，网络中每条弧对应的反向弧都体现在图中了。首先对其建立层次图：
   
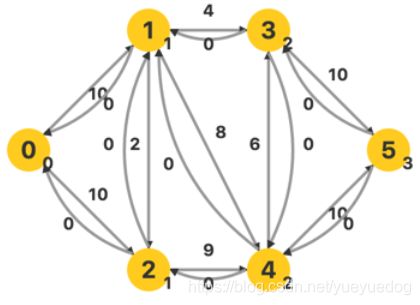
   每个顶点右下方的数字就是其对应的层次。接下来进行 DFS ，找到一条流量为 4 的增广路：
   
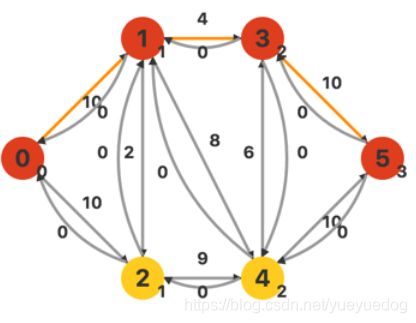
   回退至顶点 3，发现它没有其他的允许弧，继续回退至 1 。在回退的过程中不断修改流经的弧的容量。接下来，发现顶点 1 有一个允许弧连至 4，继续 DFS 。注意，此时流量上限已经更新为 10 − 4 = 6。
   
   又找到一条流量为 min(6, 8, 10) = 6 的增广路。
   顶点 1 的流量上限已经为 0，从顶点 1 回退至源点。修改相关弧的剩余容量。
   
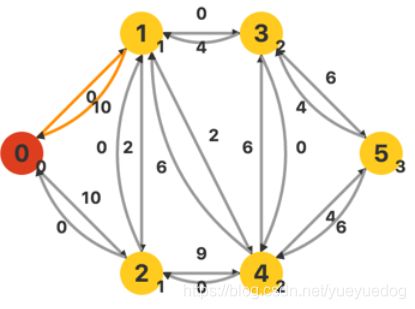
   继续搜索源点的相邻顶点 2，并找到一条增广路。由于源点的容量上限始终是 INF ，所以增广路的流量为 min(10, 9, 4) = 4。
   
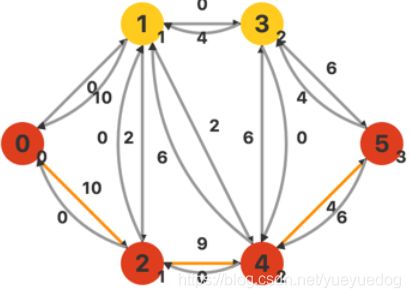
   回退至源点，调整对应弧的容量。发现源点没有其他相邻顶点， DFS 过程结束。
   
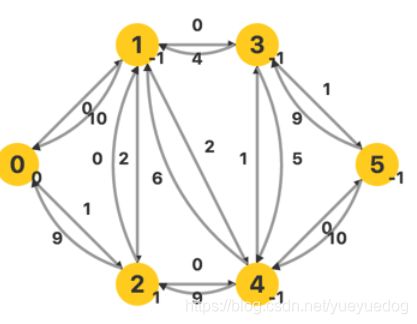
   再次 BFS，建立层次图。我们发现，顶点 1 的层次变成了 3 ，和上一次有所不同。
   
   找到一条增广路，流量为 min(6, 5, 6, 6) = 5 。
   发现没有其他增广路，回退至源点，更新相关弧的容量。
   

进行 BFS，发现汇点不再在层次网络中，算法结束。最大流为 4 + 6 + 4 + 5 = 19。

实现 Dinic 算法

#include 
#include 
#include 
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAX_N = 100;
const int MAX_M = 10000;
struct edge {
     
    int v, c, fail;
} e[MAX_M];
int p[MAX_N], eid;
void init() {
     
    memset(p, -1, sizeof(p));
    eid = 0;
}
void insert(int u, int v, int c) {
     
    e[eid].v = v;
    e[eid].fail = p[u];
    e[eid].c = c;
    p[u] = eid++;
}
void addedge(int u, int v, int c) {
     
    insert(u, v, c);
    insert(v, u, 0);
}