数据结构---栈
文章目录
- 1.1 栈的概念及结构
- 1.2 栈的实现
-
- 1.2.1顺序表和链表实现栈不同及优缺点
- 1.3 数组实现栈的完整代码
- 1.4 栈的相关选择题
- 1.5 LeetCode第20题---有效的括号
1.1 栈的概念及结构
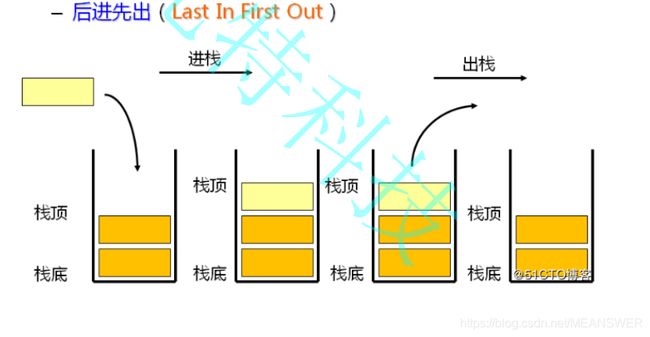
栈:一种特殊的线性表,其只允许在固定的一段进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出的原则。
压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶
1.2 栈的实现
栈的实现一般可以使用数组或者链表实现,相对而言数组的结构实现栈更优一些。因为数组在尾上插入数据的代价比较小。
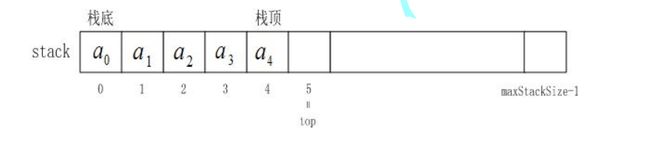
使用数组来实现栈,你可以认为最开始的时候栈底和栈顶在同一个位置处,但是栈顶更像是形容入栈的方向,表示着入栈数据的走向。
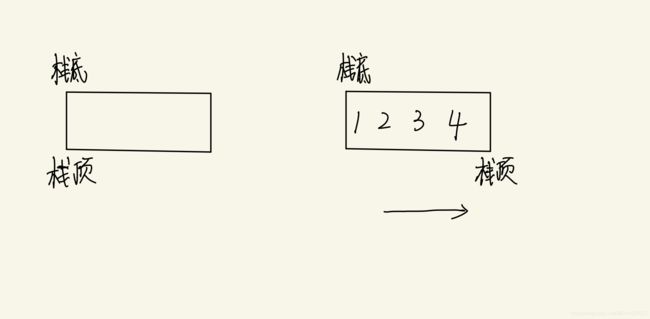
1.2.1顺序表和链表实现栈不同及优缺点
那么为什么使用数组会比使用链表更加的优呢?
对于数组结构来表示栈,是不能够进行头插和中间插入的,因为会破坏栈的后进先出的特点。那么你可能就会想:使用顺序表需要增容,或者会造成空间的浪费等…事实上对于一个顺序表来说并不是你每次插入数据都需要进行增容的操作,而且对于计算机来说内存是相当大的,你就算浪费了几百几千个字节的空间大小对于他来说也是微不足道的,除非你从事的是嵌入式的行业,对于内存非常看重,那么就另当别论了,最主要的就是顺序表容易实现。如果是双向链表,那一边是栈顶那一边是栈底其实都是可以的。但是如果是单链表,你的头处应该设置为栈顶的方向。
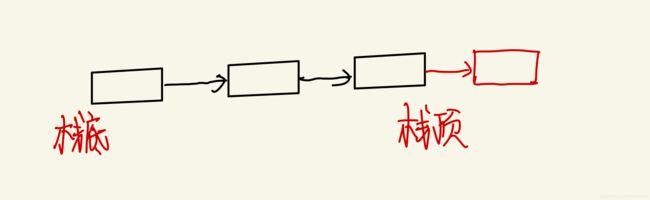
如果你所定义的是单链表实现栈的结果是这样子,你就会发现,你在栈顶插入数据,但是当你想要Pop的时候,他的前一个地址你是不知道的。

什么时候会使用到栈呢?
比如说后入先出的场景,对于一个迷宫来说,有时候我可能会走到死胡同,此时我希望它能够退回到原来的位置,我就可以用这个来实现。
1.3 数组实现栈的完整代码
#pragma once
#include#include"Stack.h"
//初始化
void StackInit(Stack* pst)
{
assert(pst);
//这种方式是有不好的地方的,因为但当你需要增容的时候,你就会发现,他的capacity初始化是0,那么你乘2依旧是0,所以建议一开始就给一个固定值
//pst->_a = NULL;
//pst->_top = 0;
//pst->_capacity = 0;
pst->_a = (STDateType*)malloc(sizeof(STDateType)*4);
pst->_top = 0;
pst->_capacity = 4;
}
//销毁
void StackDestory(Stack* pst)
{
assert(pst);
free(pst->_a);
pst->_a = NULL;
pst->_top = pst->_capacity = 0;
}
//入栈
//只要入栈就要考虑到空间是否满的情况,对其进行判断
void StackPush(Stack* pst, STDateType x)
{
assert(pst);
//空间不够则增容
if (pst->_top == pst->_capacity)
{
pst->_capacity *= 2;
STDateType* tmp = (STDateType*)realloc(pst->_a, sizeof(STDateType)*pst->_capacity);
if (tmp == NULL)
{
printf("内存不足\n");
exit(-1);
}
else
{
pst->_a = tmp;
}
}
pst->_a[pst->_top] = x;//你所定义的栈顶总是在你放入数据的下一个位置
pst->_top++;
}
//出栈
void StackPop(Stack* pst)
{
assert(pst);
assert(pst->_top > 0);//得确保栈里面是有数据的,你才能去删
--pst->_top;
}
//获取数据个数
int StackSize(Stack* pst)
{
assert(pst);
return pst->_top;
}
//返回1是空,返回0是非空
int StackEmpty(Stack* pst)
{
assert(pst);
return pst->_top == 0 ? 1 : 0;
}
//获取栈顶的数据
STDateType StackTop(Stack* pst)
{
assert(pst);
assert(pst->_top > 0);
return pst->_a[pst->_top - 1];//你所定义的栈顶总是在你放入数据的下一个位置
}
#include"Stack.h"
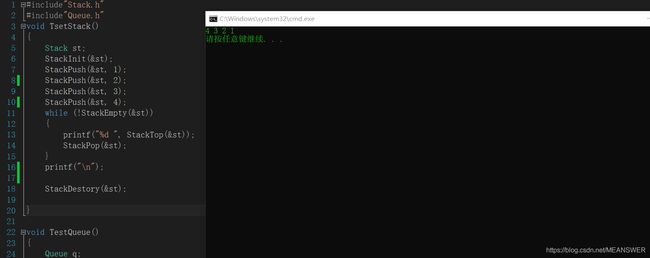
void TsetStack()
{
Stack st;
StackInit(&st);
StackPush(&st, 1);
StackPush(&st, 2);
StackPush(&st, 3);
StackPush(&st, 4);
while (!StackEmpty(&st))
{
printf("%d ", StackTop(&st));
StackPop(&st);
}
printf("\n");
StackDestory(&st);
}
int main()
{
TsetStack();
return 0;
}
栈并没有规定要求一次性入栈或者出栈,你可以选择边入边出。所以一个入栈的顺序可能对应着多个出栈的顺序。
1.4 栈的相关选择题
1.一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈,然后再依次出栈,则元素出栈的顺序是( B)。
A 12345ABCDE
B EDCBA54321
C ABCDE12345
D 54321EDCBA
这些答案都是如果题目没有出现“依次”这个词的情况下的结果,但是当出现“依次”的时候结果只可能是B,一次全部入栈,然后在全部出栈
A:对于A选项就是入栈一个出栈一个,是可能出现的结果
B:一次性全部入栈,然后在全部出栈,是有可能出现的结果
C:不可能
D:先入12345然后出栈,然后载入ABCDE然后出栈,是有可能出现的结果
2.若进栈序列为 1,2,3,4 ,进栈过程中可以出栈,则下列不可能的一个出栈序列是(C)
A 1,4,3,2
B 2,3,4,1
C 3,1,4,2
D 3,4,2,1
答案:
A:先入1,出1,然后入2,3,4在出栈,是可能出现的结果。
B:先入1,2然后出栈2,然后在入3,出3,入4出4,最后出1,是可能的结果。
C:不可能。
D入1,2,3出3,然后入4,出4,再出2,1是可能出现的结果。
1.5 LeetCode第20题—有效的括号


对于C++来说自己就有栈,但是对于c语言来说是没有栈的,还需要自己来实现一个栈才行
typedef char STDateType;
typedef struct Stack
{
STDateType* _a;
int _top; //栈顶下标
int _capacity;
}Stack;
//初始化和销毁
void StackInit(Stack* pst);
void StackDestory(Stack* pst);
//入栈
void StackPush(Stack* pst, STDateType x);
//出栈
void StackPop(Stack* pst);
//获取数据个数
int StackSize(Stack* pst);
//返回1是空,返回0是非空
int StackEmpty(Stack* pst);
//获取栈顶的数据
STDateType StackTop(Stack* pst);
//初始化
void StackInit(Stack* pst)
{
assert(pst);
pst->_a = (STDateType*)malloc(sizeof(STDateType)*4);
pst->_top = 0;
pst->_capacity = 4;
}
//销毁
void StackDestory(Stack* pst)
{
assert(pst);
free(pst->_a);
pst->_a = NULL;
pst->_top = pst->_capacity = 0;
}
//入栈
void StackPush(Stack* pst, STDateType x)
{
assert(pst);
//空间不够则增容
if (pst->_top == pst->_capacity)
{
pst->_capacity *= 2;
STDateType* tmp = (STDateType*)realloc(pst->_a, sizeof(STDateType)*pst->_capacity);
if (tmp == NULL)
{
printf("内存不足\n");
exit(-1);
}
else
{
pst->_a = tmp;
}
}
pst->_a[pst->_top] = x;//你所定义的栈顶总是在你放入数据的下一个位置
pst->_top++;
}
//出栈
void StackPop(Stack* pst)
{
assert(pst);
assert(pst->_top > 0);
--pst->_top;
}
//获取数据个数
int StackSize(Stack* pst)
{
assert(pst);
return pst->_top;
}
//返回1是空,返回0是非空
int StackEmpty(Stack* pst)
{
assert(pst);
return pst->_top == 0 ? 1 : 0;
}
//获取栈顶的数据
STDateType StackTop(Stack* pst)
{
assert(pst);
assert(pst->_top > 0);
return pst->_a[pst->_top - 1];//你所定义的栈顶总是在你放入数据的下一个位置
}
bool isValid(char * s){
Stack st;
StackInit(&st);
while(*s != '\0')
{
//如果是前括号那就入栈,如果是后括号那就拿栈顶的值和此时相比较(这样他们两个才是相邻的)
if(*s == '[' || *s == '(' || *s == '{')
{
StackPush(&st,*s);
s++;
}
else
{
//表示此时前括号栈里没有了,但是]还有 []]]
if(StackEmpty(&st))
return false;
//取栈顶
char top = StackTop(&st);
if(*s == ']' && top != '[')
return false;
if(*s == ')' && top != '(')
return false;
if(*s == '}' && top != '{')
return false;
StackPop(&st);
s++;
}
}
//这里的while循环结束有两种情况:一种就是你的s遍历完了, 这种情况[[[] [在栈里面还有。还有一种就是都匹配上了,里面不再有任何东西了
//这里判断的是[[[] 在栈里面还有,但是你的s已经遇见了'\0'遍历完了
int ret = StackEmpty(&st);
// ret如果为1表示空,此时所有的括号都匹配上了,1就代表true,但是ret加上下面这个ret==0这个判断条件更加容易理解,如果他是0表示[在栈里面还有,但是此时s已经遍历完了,所以他不为空,那么也是一种错误的情况
if(ret == 0)
return false;
//在你把栈使用完了以后一定要对其进行释放,否则就会造成内存的泄漏
StackDestory(&st);
return ret;
}