Pytorch学习笔记（一）自用

涉及资源
1.官网DEEP LEARNING WITH PYTORCH: A 60 MINUTE BLITZ
2.莫烦python 个人网站 、 b站视频、参考代码
3.函数搜索：https://pytorch.org/docs/stable/index.html

系列学习笔记：
Pytorch学习笔记（一）
Pytorch学习笔记（二）
Pytorch学习笔记（三）

本周学习内容：
Numpy torch对比
激励函数
pytorch实现Regression
pytorch实现Classification
pytorch快速搭建法实现Classification
pytorch实现网络的保存与提取
pytorch实现batch_train
pytorch实现optimizer性能比对
pytorch实现CNN，识别MNIST数据集

环境配置：
python=3.7; torch=1.6.0; torchvision=0.7.0

1、Regression

import torch
from torch.autograd import Variable
import torch.nn.functional as F # 拿到一些激励函数
import matplotlib.pyplot as plt

## data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # unsqueeze多加一维，因为Variable输入为二维
y = x.pow(2) + 0.2 * torch.rand(x.size())
# x, y = Variable(x), Variable(y) # 放在Varible的篮子里

# plt.scatter(x.data.numpy(), y.data.numpy())
# plt.show()

## NET
class Net(torch.nn.Module): # 继承torch的模块
    def __init__(self, n_feature, n_hidden, n_output):# 定义层
        super(Net, self).__init__()# 调用父类的初始化
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):# 前向传递，搭建神经网络,x = inputData
        x = F. relu(self.hidden(x))
        x = self.predict(x) # 回归预测的时候一般不用激励函数，加了relu无法预测负值
        return x

## 训练 + 可视化过程
net = Net(1, 15, 1)
print(net)

plt.ion() # 实时打印
plt.show()

optimizer = torch.optim.SGD(net.parameters(), lr=0.5) # 网络优化.lr一般小于1
# loss_func = F.mse_loss()# 均方差

for t in range(100):# 训练100步
    prediction = net(x)# output

    loss = F.mse_loss(prediction, y)
    # 优化
    optimizer.zero_grad() # clear gradients for this training 
    loss.backward() # backpropagation, compute gradients
    optimizer.step() # apply gradients

    if t % 5 == 0:# 学习五步打印一次
        plt.cla()# 清空
        plt.scatter(x.data.numpy(), y.data.numpy())# 散点图
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'loss = %.4f' % loss.data.numpy(), fontdict={
     'size': 20, 'color': 'red'})
        plt.pause(0.1)
    plt.ioff()
    plt.show()

print(net)

Net(
(hidden): Linear(in_features=1, out_features=15, bias=True)
(predict): Linear(in_features=15, out_features=1, bias=True)
)

2、CLassification

import torch
from torch.autograd import Variable
import torch.nn.functional as F # 拿到一些激励函数
import matplotlib.pyplot as plt

## make fake data
n_data = torch.ones(100, 2)
x0 = torch.normal(2*n_data, 1)      # class0 x data (tensor), shape=(100, 2)
y0 = torch.zeros(100)               # class0 y data (tensor), shape=(100, 1)
x1 = torch.normal(-2*n_data, 1)     # class1 x data (tensor), shape=(100, 2)
y1 = torch.ones(100)                # class1 y data (tensor), shape=(100, 1)
# 数据和标签转换为 torch 中默认的形式
x = torch.cat((x0, x1), 0).type(torch.FloatTensor)  # shape (200, 2) FloatTensor = 32-bit floating; cat合并
y = torch.cat((y0, y1), ).type(torch.LongTensor)    # shape (200,) LongTensor = 64-bit integer
# 现在autograd 直接支持tensors了
# x, y = Variable(x), Variable(y) # 放在Varible的篮子里

plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=50, lw=0, cmap='RdYlGn')
plt.show()

## method 1
class Net(torch.nn.Module): # 继承torch的模块
    def __init__(self, n_feature, n_hidden, n_output):# 定义层
        super(Net, self).__init__()# 调用父类的初始化
        self.hidden = torch.nn.Linear(n_feature, n_hidden)
        self.predict = torch.nn.Linear(n_hidden, n_output)

    def forward(self, x):# 前向传递，搭建神经网络,x = inputData
        x = F. relu(self.hidden(x))
        x = self.predict(x) # 回归预测的时候一般不用激励函数，加了relu无法预测负值
        return x

## 训练 + 可视化过程
net1 = Net(2, 10, 2)

## method 2
net2 = torch.nn.Sequential(# 一层一层
    torch.nn.Linear(2, 10),
    torch.nn.ReLU(),# 区别
    torch.nn.Linear(10, 2),
)
print(net1)
print(net2)

plt.ion() # 实时打印
plt.show()

optimizer = torch.optim.SGD(net2.parameters(), lr=0.01) # 网络优化.lr一般小于1

for t in range(100):# 训练100步
    out = net2(x)

    loss = F.cross_entropy(out, y) # 交叉熵，用于多分类问题

    # 优化
    optimizer.zero_grad() # pytorch计算梯度不是覆盖，与上一次的求和，net.parameters手动清0
    loss.backward() # Variable反向传递
    optimizer.step() # 更新参数

    if t % 2 == 0:
        # plot and show learning process
        plt.cla()
        prediction = torch.max(out, 1)[1] # softmax变成prediction,概率
        pred_y = prediction.data.numpy()
        target_y = y.data.numpy()
        plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
        accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
        plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={
     'size': 20, 'color': 'red'})
        plt.pause(0.1)

    plt.ioff()
    plt.show()

print(net1)

Net(
(hidden): Linear(in_features=2, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=2, bias=True)
)

print(net2)

Sequential(
(0): Linear(in_features=2, out_features=10, bias=True)
(1): ReLU()
(2): Linear(in_features=10, out_features=2, bias=True)
）

3、save_reload

import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
# torch.manual_seed(1)    # reproducible

# data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())  # noisy y data (tensor), shape=(100, 1)
# Pytorch 0.4可以直接用tensors
# x, y = Variable(x, requires_grad=False), Variable(y, requires_grad=False)

def save():
    # save net1
    net1 = torch.nn.Sequential(
        torch.nn.Linear(1, 10),
        torch.nn.ReLU(),
        torch.nn.Linear(10, 1)
    )
    optimizer = torch.optim.SGD(net1.parameters(), lr=0.5)
    # loss_func = torch.nn.MSELoss()

    for t in range(100):
        prediction = net1(x)
        loss = F.mse_loss(prediction, y)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

    # plot result
    plt.figure(1, figsize=(10, 3))
    plt.subplot(131)
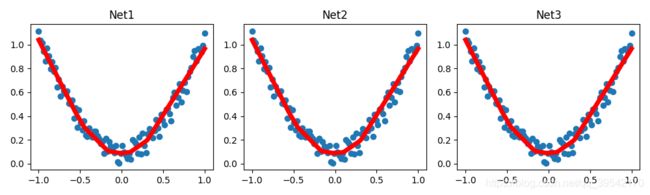
    plt.title('Net1')
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)

    # 2 ways to save the net
    torch.save(net1, 'net.pkl')  # save entire net,以pkl形式保存
    torch.save(net1.state_dict(), 'net_params.pkl')   # save only the parameters

def restore_net():
    net2 = torch.load('net.pkl')
    prediction = net2(x)

    # plot result
    plt.subplot(132)
    plt.title('Net2')
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)

def restore_params():
    net3 = torch.nn.Sequential(
        torch.nn.Linear(1, 10),
        torch.nn.ReLU(),
        torch.nn.Linear(10, 1)
    )
    # copy net1's parameters into net3
    net3.load_state_dict(torch.load('net_params.pkl'))
    prediction = net3(x)

    # plot result
    plt.subplot(133)
    plt.title('Net3')
    plt.scatter(x.data.numpy(), y.data.numpy())
    plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
    plt.show()

save()
restore_net()
restore_params()

4、batch_train

import torch
import  torch.utils.data as Data

# BATCH_SIZE = 5
BATCH_SIZE = 8
x = torch.linspace(1, 10, 10) # torch tensor
y = torch.linspace(10,1,10) # torch tensor

torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
    dataset=torch_dataset,
    batch_size=BATCH_SIZE,
    shuffle=True,#打乱数据
    num_workers=0,# 2线程
)

for epoch in range(3):
    for step, (batch_x, batch_y) in enumerate(loader):
        # training
        print('Epoch: ',epoch,'| Step: ', step, '| batch x: ',batch_x.numpy(), '| batch y: ', batch_y.numpy())

数据个数为10，BATCH_SIZE = 8，EPOCH = 3时

Epoch: 0 | Step: 0 | batch x: [ 2. 1. 8. 9. 4. 5. 10. 3.] |batch y: [ 9. 10. 3. 2. 7. 6. 1. 8.]
Epoch: 0 | Step: 1 |batch x: [6. 7.] | batch y: [5. 4.]
Epoch: 1 | Step: 0 | batch x: [ 1. 10. 6. 9. 2. 5. 4. 8.] | batch y: [10. 1. 5. 2. 9. 6.7. 3.]
Epoch: 1 | Step: 1 | batch x: [3. 7.] | batch y: [8. 4.]
Epoch: 2 | Step: 0 | batch x: [ 4. 7. 10. 8. 9. 6. 5. 2.] | batch y: [7. 4. 1. 3. 2. 5. 6. 9.]
Epoch: 2 | Step: 1 | batch x: [1. 3.] | batch y: [10. 8.]

数据个数为10，BATCH_SIZE = 5，EPOCH = 3时

Epoch: 0 | Step: 0 | batch x: [ 7. 10. 5. 1. 8.] | batch y: [4. 1. 6. 10. 3.]
Epoch: 0 | Step: 1 | batch x: [6. 3. 2. 9. 4.] | batch y: [5. 8. 9. 2. 7.]
Epoch: 1 | Step: 0 | batch x: [4. 7. 2. 5. 1.] | batch y: [ 7. 4. 9. 6. 10.]
Epoch: 1 | Step: 1 | batch x: [ 9. 10. 8. 3. 6.] | batch y: [2. 1. 3. 8. 5.]
Epoch: 2 | Step: 0 | batch x: [ 7. 4. 8. 10. 1.] | batch y: [ 4. 7. 3. 1. 10.]
Epoch: 2 | Step: 1 | batch x: [6. 5. 9. 3. 2.] | batch y: [5. 6. 2. 8. 9.]

5、optimizer

import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt

# hyper para
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12

# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)# unsqueeze多加一维
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))

# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
    dataset=torch_dataset,
    batch_size=BATCH_SIZE,
    shuffle=True,  # 打乱数据
    num_workers=0,  # 2线程
)

# default network
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = torch.nn.Linear(1, 20)   # hidden layer
        self.predict = torch.nn.Linear(20, 1)   # output layer

    def forward(self, x):
        x = F.relu(self.hidden(x))      # activation function for hidden layer
        x = self.predict(x)             # linear output
        return x

if __name__ == '__main__':
    # different nets
    net_SGD = Net()
    net_Momentum = Net()
    net_RMSprop = Net()
    net_Adam = Net()
    nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam] #放在一个list当中

    # different optimizers
    opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
    opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
    opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
    opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
    optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]

    losse_his = [[],[],[],[]] # record loss

    for epoch in range(EPOCH):
        print(epoch)
        for step,(batch_x, batch_y) in enumerate(loader):
            for net, opt, l_his in zip(nets, optimizers, losse_his):
                output = net(batch_x)  # get output for every net
                loss = F.mse_loss(output, batch_y)  # compute loss for every net
                l_his.append(loss.data.numpy())  # loss recoder

                opt.zero_grad()  # clear gradients for next train
                loss.backward()  # backpropagation, compute gradients
                opt.step()  # apply gradients

    labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
    for i, l_his, in enumerate(losse_his):
        plt.plot(l_his, label=labels[i])
    plt.legend(loc='best')
    plt.xlabel('Steps')
    plt.ylabel('Loss')
    plt.ylim((0, 0.2))
    plt.show()

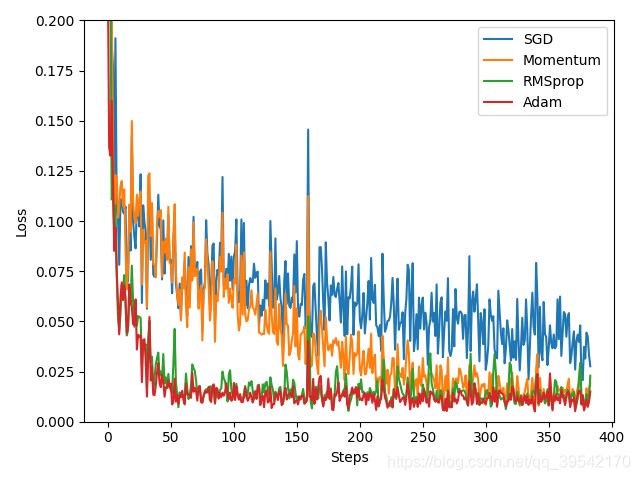
优化器理论可参考：https://blog.csdn.net/weixin_40170902/article/details/80092628